11-12. Taylor and Maclaurin Polynomials
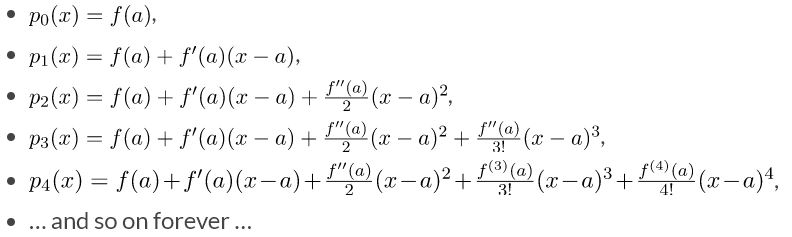


13. Sequences
Arithmetic Sequence:

Geometric Sequence:
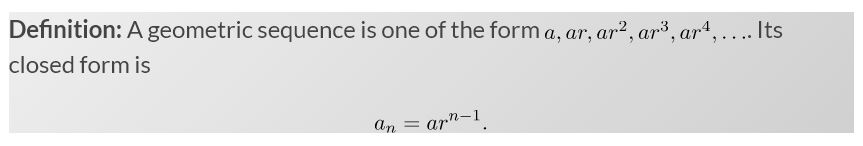

Convergence of Sequence:
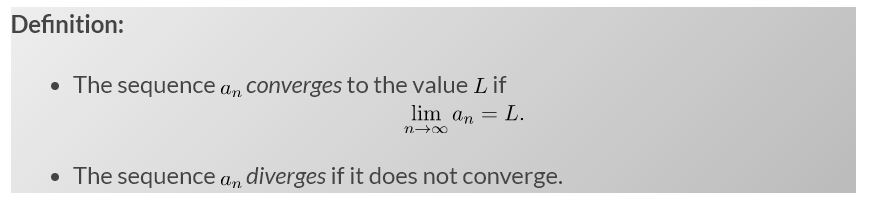

14. Infinite Series
Infinite Sequence:
If a sequence is a list of numbers: … then a series is just the sum of the terms in the series: …
Infinite Series:
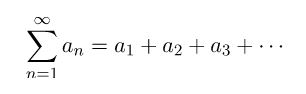
Geometric Series:

Partial Sum of Geometric Series:
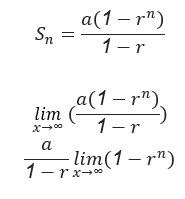
Converging and Diverging Series:
For the infinite series 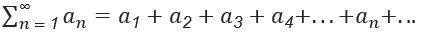
the nth partial sum is given by 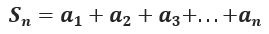
If the sequence of partial sums converges to L,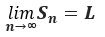 then the series converges where L is the sum of the series.
then the series converges where L is the sum of the series.
If 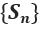 diverges, then the series diverges.
diverges, then the series diverges.
Divergent Test for a Series:
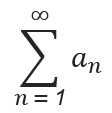

Telescoping Infinite Series:
The telescoping series is of the form
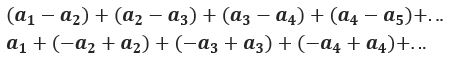
The series will only converge if and only if 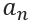 approaches a finite number as n approaches infinity.
approaches a finite number as n approaches infinity.
15. The Divergence and Integral Tests:
Integral Test:

- The interval does not always need to start at 1.
- The function does not necessarily always need to be decreasing. It needs to decrease for the x-value larger than 1.
P-Series Test:

Divergence Test:

16. Comparison Tests:
Comparison Test:
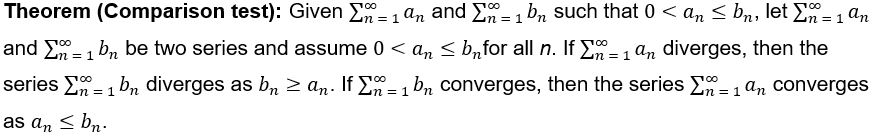
Limit Comparison Test:

17. Alternating Series Test:
Alternating Series Test:

The alternating series test applies to the alternating harmonic series 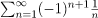 because the individual terms satisfy the three conditions:
because the individual terms satisfy the three conditions:
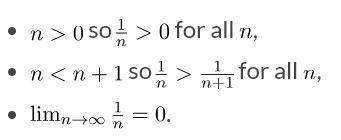
So the alternating harmonic series  converges by the alternating series test.
converges by the alternating series test.
Absolute and Conditional Convergence:

This means that there are three possibilities for any given series: the series either converges absolutely or conditionally, or the series diverges.
18. Ratio and Root Test:
Ratio Test:

Root Test:

19. Power Series and Functions & Properties of Power Series:
Power Series:

Interval of Convergence:

20. Taylor and Maclaurin Series & Working with Taylor Series:
Taylor Series
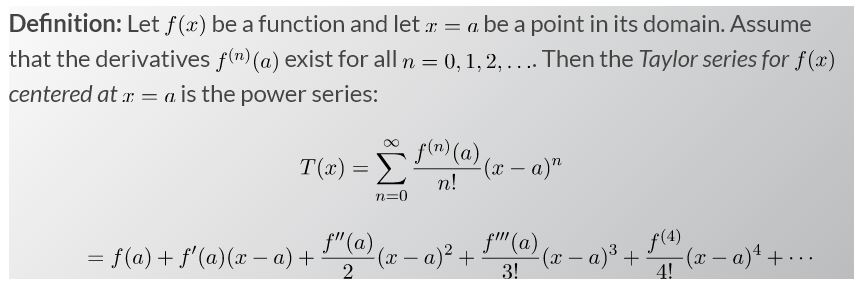
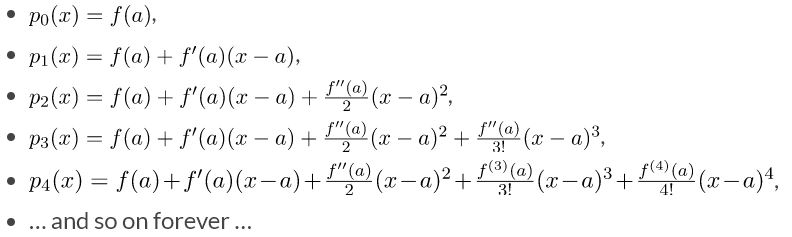



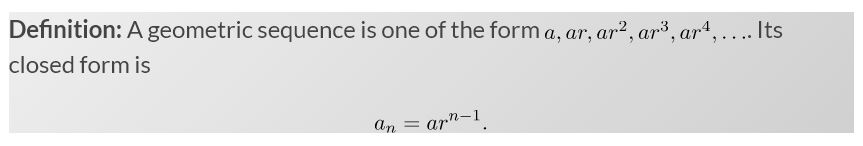

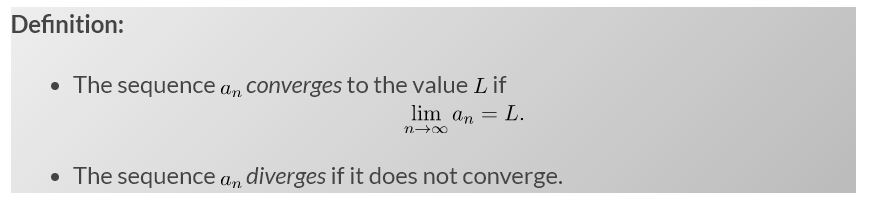

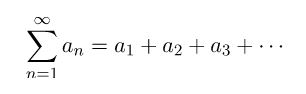

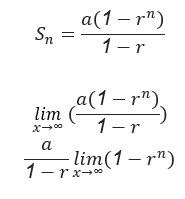
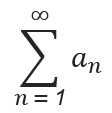

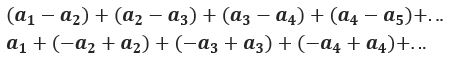



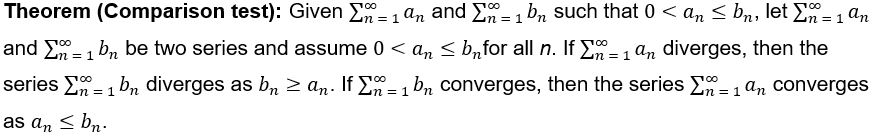


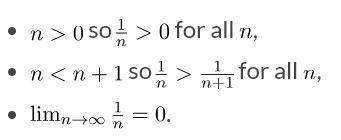





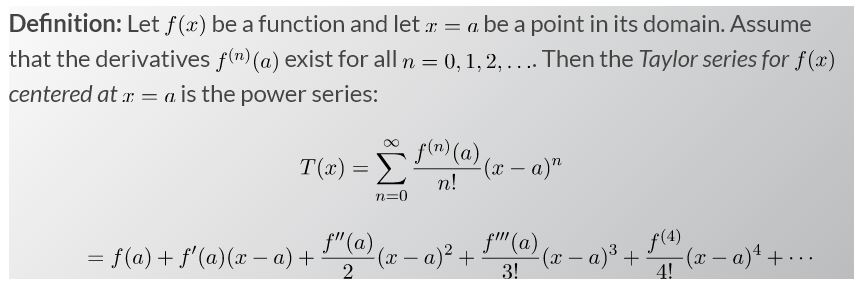



Recent Comments