Group Members Present:
Zanab Alawlaqi
Brygetee Al-Shawkani
Eduardo Luis Berroa-Wisky
Mamadou Bah
Aleem Ahmed
Community Agreement: As a group, we decided that in terms of our group’s community agreement, we decided that we would keep the agreement as is.
Standard 3: Evaluate definite and indefinite integrals using trigonometric substitution
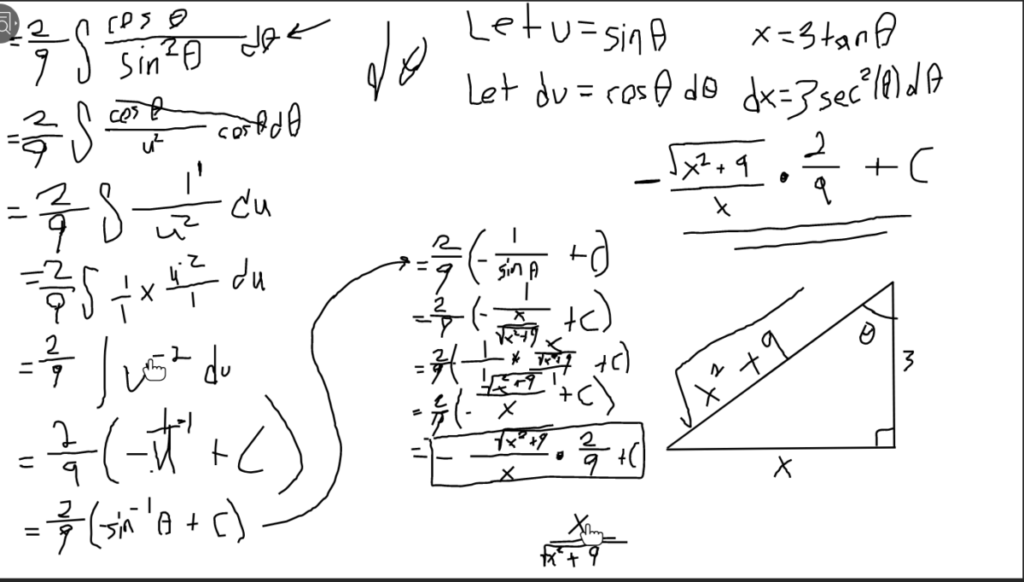
- The first step after identifying which problem fit standard three was to substitute x for 6tan theta. Theta became arctan (x/6) and dx became 6sec^2 theta. This is one of the most important steps because if you don’t properly substitute in the beginning of the problem, you won’t be able to find the right answer. We chose to use this because the square root was in the form (a^2 + x^2).
- Next we replaced the value under the square root with 36sec^2theta, leaving us with the integral 1/36 integral of sec theta / tan^2 theta.
- This could easily be converted to cos theta/ sin^2theta.
- Next we did u substitution where u = sin theta, du= cos theta and dtheta = 1/Cos theta.
- This integral became 1/u^2 which we solved to be -1/v.
- Undoing the u substitution and adding the 1/36 from the earlier part of the problem, the problem became -1/36sintheta.
- Undoing all previous substitution we were left with -square root(x^2+36)/36x+c.
Standard 4: Evaluate definite and indefinite integrals using partial fraction decomposition
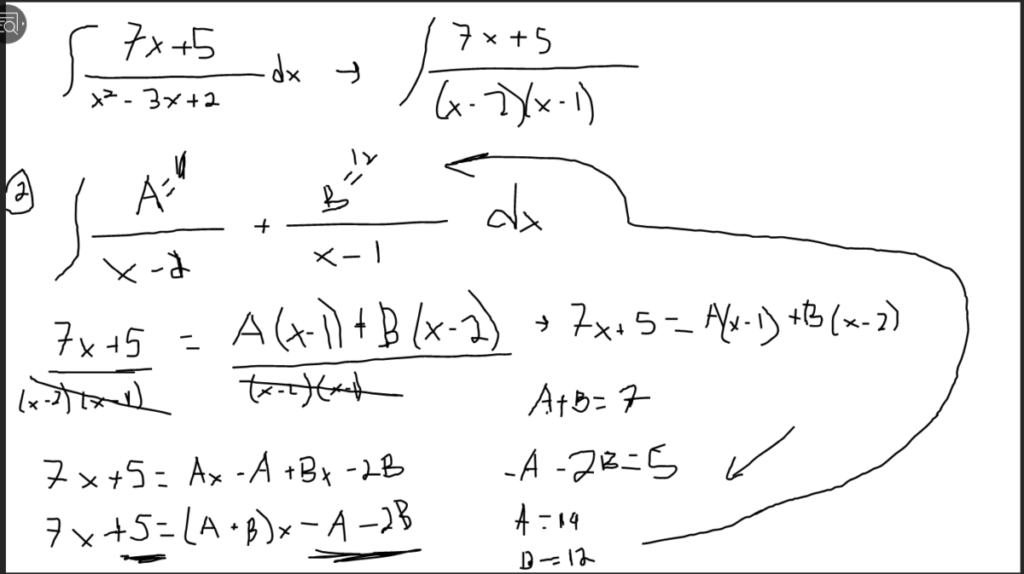
Step #1: Factor out the denominator of the indefinite integral, equation x2-3x+2which is equivalent to (x-1)(x-2).
Step #2: Separate the numerator above, equation 9x+7 corresponding two factorial denominators below: (x-1) and (x-2) where 9x becomes A and 7 becomes B.
Step #3: Make (9x+7)/(x-1)(x-2)equal to A/(x-1)+B/(x-2)then multiply them with the common denominator (x-1)(x-2). As a result, the denominator cancels out on both sides, leaving 9x+7 = A(x-2) + B(x-1).
Step #4: Factor A with the equation (x-2) and factor B with the equation (x-1), there the equation is Ax-2A+Bx-1B.
Step #5: Before plugging in the x-variables, subtract the two equations (x-2) and (x-1) by zero. From there, x = 2 and x = 1.
Step #6: For equation 9x+7 = Ax-2A+Bx-1B, replace the x-variables with the following:
x = 2 and x = 1.
For x = 2, 9(2)+7 = A(2)-2A+B(2)-1B
18+7 = 2A-2A+2B-1B; as a result, 2A cancels each other out.
25 = 1B -> 25/1 = 1B/1-> B = 25
For x = 1, 9(1)+7 = A(1)-2A+B(1)-1B
9+7 = 1A-2A+1B-1B; as a result, 1B cancels each other out.
16 = -1A -> 16/-1=-1A/-1->A = -16
Step #7: For the indefinite integral (Ax-1+Bx-2)dx, replace A with -16 and replace B with 25. Therefore, the indefinite integral is now (-16x-1+25x-2)dx.
Step #8: Since the equation is within the parenthesis, distribute the integral by multiplying with equation -16x-1and equation 25x-2. From there, the integral equation becomes
-16x-1dx+25x-2dx.
Step #9: Extract -16 from of the integral of 1x-1dx and also, extract 25 from of the integral of 1x-2dx before integrating.
Step #10: The integral of 1x-1dxbecomes ln|x-1| and the integral of 1x-2dxbecomes ln|x-2|. Finally, the answer is
-16ln|x-1|+25ln|x-2|+C
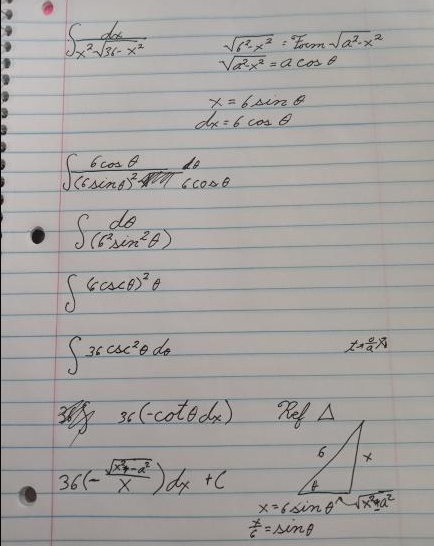


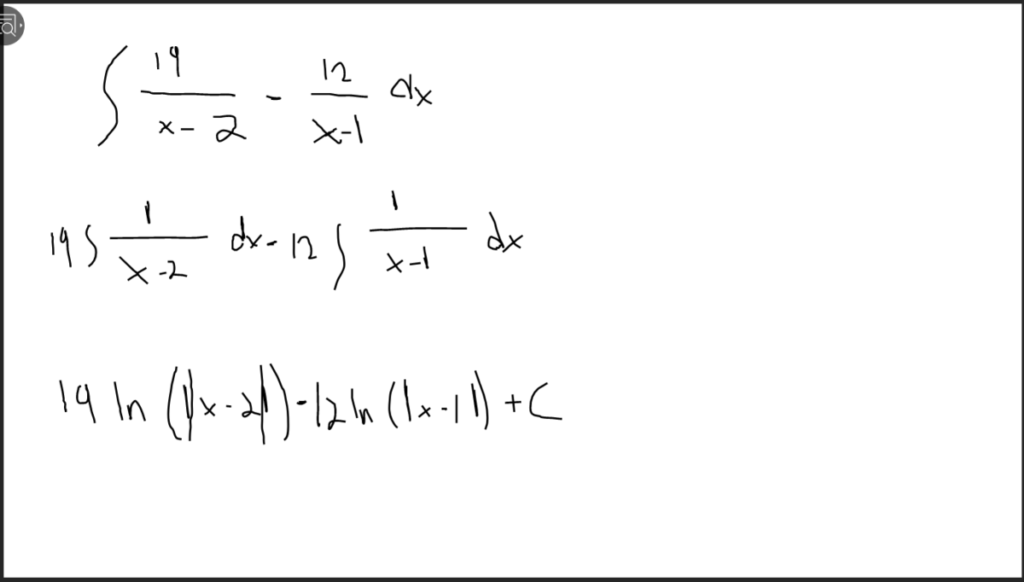



Recent Comments