We needed to use Bayes’ Theorem to solve HW7 #2. In this post, I try to briefly address the following questions:
- What is Bayes’ Theorem?
- Where does it come from?
- What is the “Bayesian interpretation” of probability?
- Why is called “Bayes'” Theorem?
Also, at the bottom of the post are a handful of videos regarding Bayes Theorem (including applications to medical testing!), and links to a couple books entirely about Bayesian probability.
What is Bayes’ Theorem?
Bayes’ Theorem (or Bayes’ Rule) is following formula for computing conditional probability (screenshot taken from https://en.wikipedia.org/wiki/Bayes%27_theorem#Statement_of_theorem):
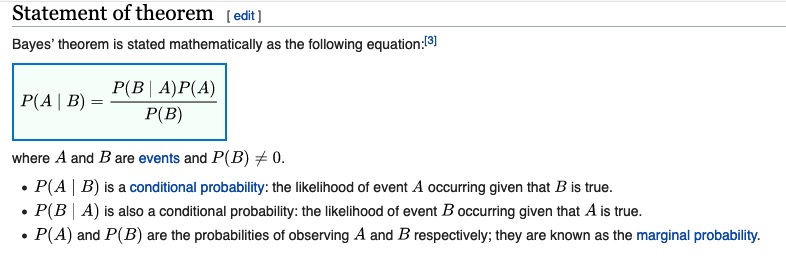
Where does Bayes’ Theorem come from?
Where does formula above for P(A | B) come from? We just have to do some algebra on the definition of conditional probability.
Start with the definition of conditional probability, applied to P(A | B) and P(B | A):
P(A | B) = P(A & B)/P(B)
P(B | A) = P(A & B)/P(A)
Now “clear the denominators” on the RHS of each equation by multiplying thru by P(B) and P(A), respectively:
P(A | B) * P(B) = P(A & B)
P(B | A) * P(A) = P(A & B)
Since the RHS is in both these equations, we know the two LHS of the equations are equal to each other!
P(A | B) = P(B | A) * P(A)/P(B)
Now just divide through by P(B) and we get Bayes’ Rule:
P(A | B) * P(B) = P(B | A) * P(A)
What is the “Bayesian interpretation” of probability?
Also from the wikipedia entry for Bayes’ Theorem

See the wikipedia entry for Bayesian probability for more on this!
Why is it called Bayes’ Rule?
One more quote from the wikipedia entry for Bayes’ Theorem:
Bayes’ theorem is named after Reverend Thomas Bayes (/beɪz/; 1701?–1761), who first used conditional probability to provide an algorithm (his Proposition 9) that uses evidence to calculate limits on an unknown parameter, published as An Essay towards solving a Problem in the Doctrine of Chances (1763). In what he called a scholium, Bayes extended his algorithm to any unknown prior cause. Independently of Bayes, Pierre-Simon Laplace in 1774, and later in his 1812 Théorie analytique des probabilités, used conditional probability to formulate the relation of an updated posterior probability from a prior probability, given evidence. Sir Harold Jeffreys put Bayes’s algorithm and Laplace’s formulation on an axiomatic basis. Jeffreys wrote that Bayes’ theorem “is to the theory of probability what the Pythagorean theorem is to geometry.”
Videos on Bayes Theorem:
Here are two introductions to Bayes Theorem:
An important application of Bayes Theorem is accuracy of medical tests–this is very timely since there is a lot of discussion about the accuracy of coronavirus testing! Here are two videos specifically on that topic:
Textbooks on Bayesian :
If you want to go even further, there are entire books devoted to Bayesian probability/statistics. Here are two introductory textbooks that look interesting (in fact, I hope to read them myself at some point!):
- “Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis”
- in particular, see here for a pdf of Ch 1, which goes through a handful of example applications
- “Bayesian Statistics the Fun Way: Understanding Statistics and Probability with Star Wars, LEGO, and Rubber Ducks”
- you could try reading Ch 7, which is available as a pdf, and which is titled “Bayes’ Theorem with LEGO”!



