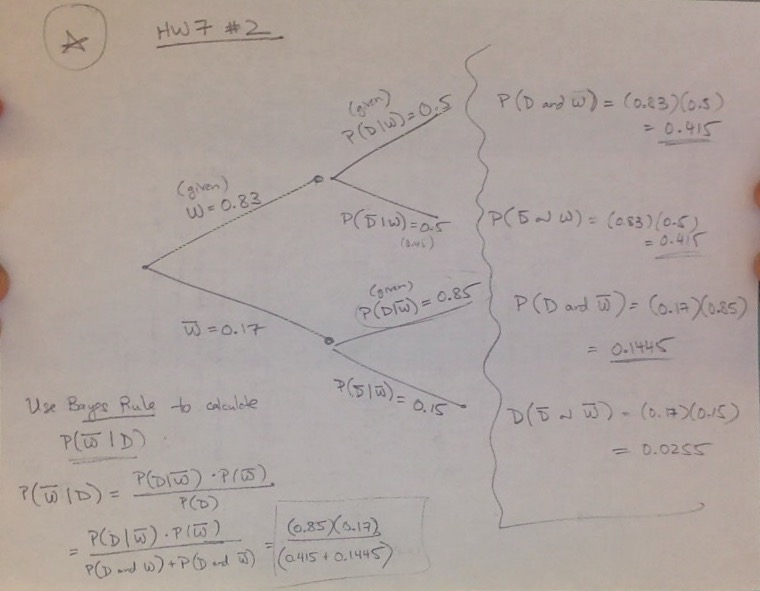
Here is a snapshot of Exercise #8 on HW7-ConditionalProbability:

The first step, as usual, is to write down the given probabilities in terms of the following events:
R = “spends time in the resource room”
“> 90” = “speends more than 90mins per week in the resource room”
Then the first two sentences tell us:
P(R) = 0.66 (and so P(not R) = 0.34)
P(> 90 | R) = 0.5
Then by the Multiplication Rule, we can compute P( > 90 ):
P(> 90) = P(> 90 | R) * P(R) = 0.5*0.66 = 0.33
(This should make sense from reading the first two sentences! If 66% of students spend time in the resource room, and half of those spend more than 90 minutes, then it should be clear that 33% of all students spend more than 90 minutes in the resource room.)
Now let’s look at what the exercise is asking us for: “If a randomly chosen student did not pass the course, what is the probability that he or she did not study in the resource room?”
We can rephrase this as “what is the probability that a randomly selected student did not study in the resource room given that the student did not pass the course?”, i.e., we need to calculate the conditional probability
P(not R | fail )
or, if we use “none” in place of “not R” (to match the label in the table), and use “F” for “fail“, we need to calculate:
P(not R | F)
We can do this using Bayes’ Theorem! Recall that Bayes’ Theorem gives us a way of calculating conditional probability:
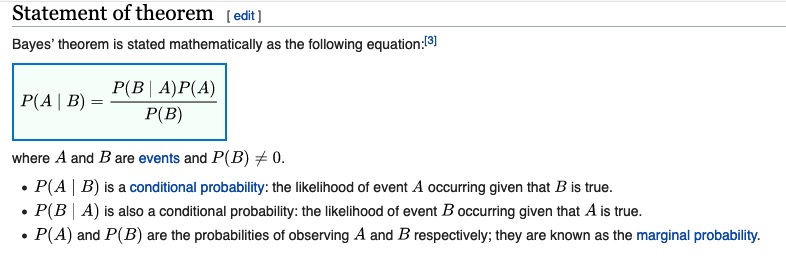
Applying this to P(not R | fail) gives us:
P(none | F) = P(F | none)*P(none) / P(F)
We can calculate the numerator as follows:
P(F | none) = 0.69 (since from the table, 31% of those those students who do not use the resource room pass)
and so
P(F | none)*P(none) = 0.69*0.34
But for the denominator P(F) we need to overall percentage of students who fail, which is not immediately given in the table. We need to calculate this by accounting for the students who fail in the three different categories (events) given in the table:
- the 69% of “none” students who fail, i.e., P(F | none) = 0.69
- the 54% of “1-90” students who fail, i.e., P(F | 1-90) = 0.54
- the 33% of “>90” students who fail, i.e., P(F | >90) = 0.33
We need to multiply each of these by the percentages of students in each category:
- 34% of the students are in the “none” category, i.e., P(none) = 0.34
- 33% of the students are in the “1-90” category, i.e., P(1-90) = 0.33
- 33% of the students are in the “>90” category, i.e., P(>90) = 0.33
Then:
P(F) = P(F | none)*P(none) + P(F | 1-90)*P(1-90) + P(F | >90)*P(>90)
= (0.69)(0.34) + (0.54)(0.33) + (0.33)(0.33)
Thus, the solution is
P(none | F) = [0.69*0.34] / [(0.69)(0.34)+(0.54)(0.33)+(0.33)(0.33)]
Note: I will post a snapshot of a tree diagram for this exercise that may help visualize these calculations!
I will also post a note about “The Law of Total Probability” which is behind the P(F) calculation above!