For the final exam, you should complete 10 exercises in the “Final Exam Exercises” WebWork set, and also submit the following written solutions and spreadsheet calculations.
The WebWork exercises and your written solutions (& spreadsheet link) are due Friday at 5pm. Good luck!
#1: Write down your calculation for “The percentage of students with over X dollars in their possession” (in terms of the frequencies shown on the histogram and the sample size n).
#2: Calculate the regression parameters in a spreadsheet. Write out the calculation of the predicted value in your written solutions.
#3: Write out each probability as a ratio of two integers, and use the “P(event)” notation.
#4: For each of the probabilities you are asked for, write down the set of outcomes in the event.
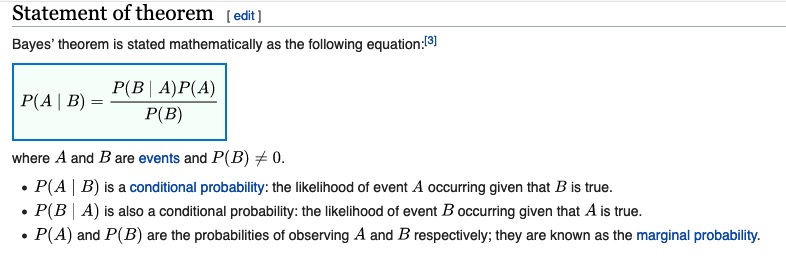
#5: Write down P(A), P(B), and P(A and B) (using the given information), and then write out the calculations of conditional probabilities asked for in the exercise (using the definition of conditional probability).
#6: Write down the calculation of the size of the sample space for this probability experiment (of choosing a committee of four at random from this group of people). Then write down the calculations of the following probabilities: (a) the committee consists of all women, and (b) the committee contains at least one man. (Hint: See Exam #3, Exercise #1.)
#7: Write down the probability distribution for the random variable X = “your net win/loss in this raffle” and write out your calculation of the expected value E[X]. (Note: WebWork requires you to include “$” in your typed solution for this exercise, and if you find the expected value is negative, include a negative sign before the dollar sign. For example, to enter an expected value of negative 50 cents, enter “-$0.50”)
#8: Write out the calculation of the expected value.
#9: Write down the values of n, p, and q for this binomial experiment. Write down the calculations of the expected value and standard deviation. (Hint: use the formulas given on the class outline and on Exam #3.)
Calculate the entire binomial probability distribution for this binomial random variable in your spreadsheet (using the spreadsheet function =binomdist(i, n, p, false)). Use your spreadsheet to calculate the probability asked for in the exercise.
#10: Sketch the normal distribution curve with the given mean and standard deviation (see the last class outline!). Indicate on your sketch the areas under the curve corresponding to the probabilities asked for in the exercise, using the notation “P(X < c)” or “P(X > c)” for each.
Finally, calculate the given probabilities in your spreadsheet (using the spreadsheet function “=normdist(c, mean, stddev, true” which outputs P(X < c)) .
You can ignore part (c) for this exercise!