Here is a snapshot of Exercise #2 on HW7-ConditionalProbability:

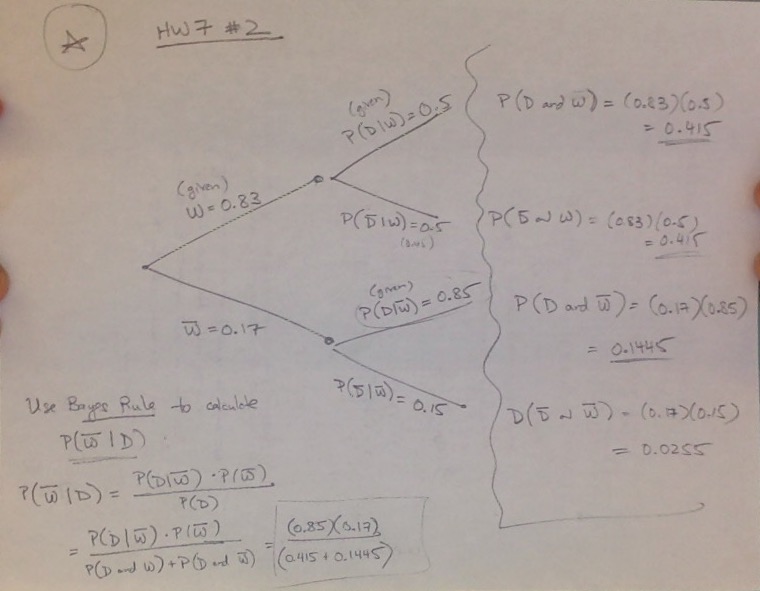
The first step with this exercise is to write down the given probabilities in terms of events that we can call:
W = neighbor waters the plant
D = plant dies
So we are given the following in the statement of the problem:
P( D | W ) = 0.5 (and so P( not D | W ) = 1 – 0.5 = 0.5)
P( D | not W ) = 0.85 (and so P( not D | W ) = 1 – 0.85 = 0.15)
Also we are given P(W) = 0.83 (and so P(not W) = 1 – 0.83 = 0.17)
We can arrange these into a tree diagram, and also use the Multiplication Rule along the branches of the tree to compute the “joint probabilities”:
P(W & D) = P(W) * P(D | W) = (0.83)(0.5) = 0.415
P(W & not D) = P(W) * P(not D | W) = (0.83)(0.5) = 0.415
P(not W & D) = P(not W) * P(D | not W) = (0.17)(0.85) = 0.1445
P(not W & not D) = P(not W) * P(not D | not W) = (0.17)(0.15) = 0.0255
(Note that these four add up to 1, as they should, since these 4 combinations cover the 4 possible outcomes! You can think of this as a probability distribution over these 4 possible outcomes.)
A tricky part of this question is interpreting what probability the question is asking for. It turns out that “What is the probability that the plant died because neighbor forgot to water it?” corresponds to P(not W | D)!
In order to compute this probability from the given probabilities, we need to apply what’s called Bayes’ Theorem, which comes from the definition of conditional probability.
(See this post for a longer introduction to Bayes’ Theorem, including its algebraic derivation from the definition of conditional probability.)
Here is a statement of Bayes’ Theorem, taken from https://en.wikipedia.org/wiki/Bayes%27_theorem#Statement_of_theorem:
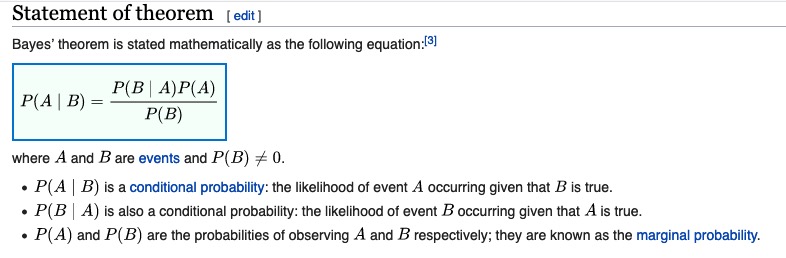
We can apply Bayes’ Theorem this to compute P(not W | D); here is the tree diagram and the calculation of P(not W | D) (in the bottom left part of the page):