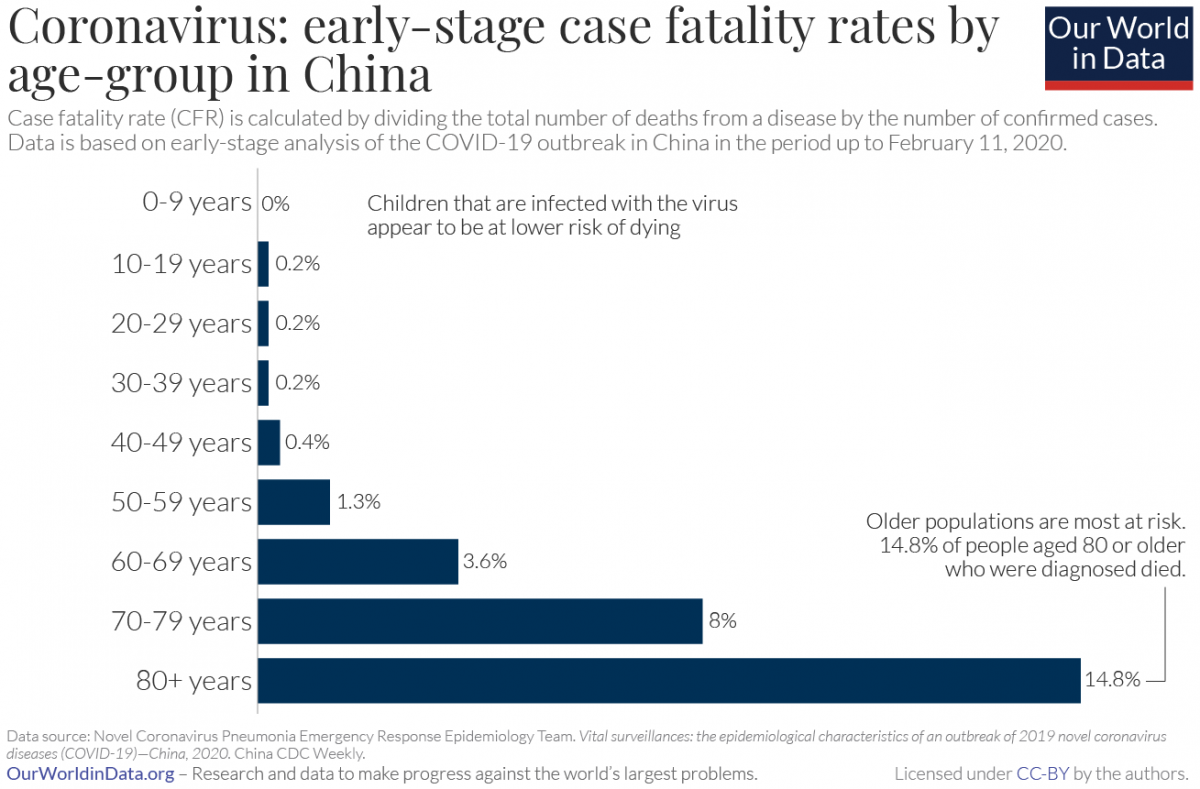
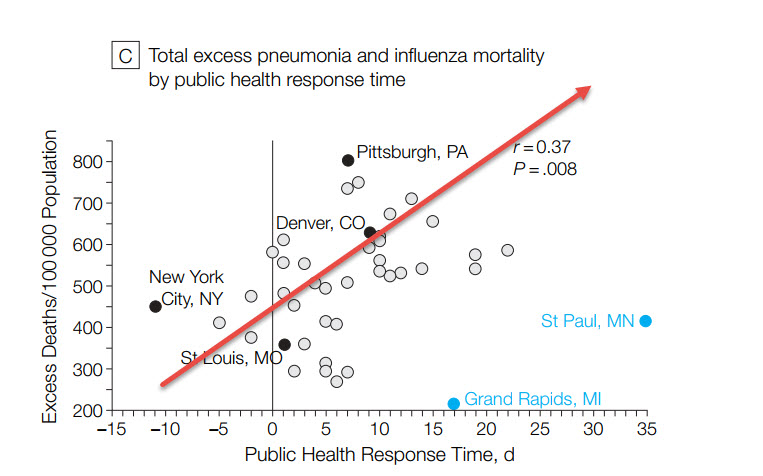
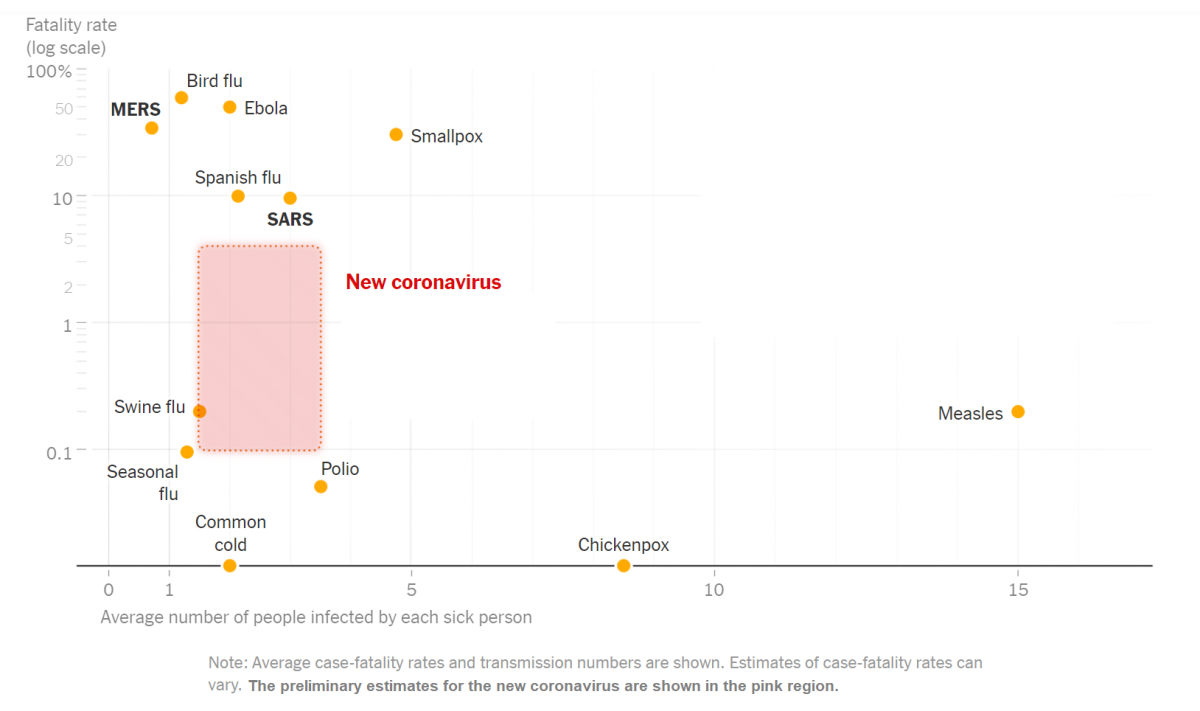
Here is a 9min video that I highly recommend you watch:
You can get a lot out of just watching the first minute: watch how he steps up the graph of the # of COVID-19 cases (outside mainland China) from Jan 22 to March 6, and shows that C(n+1) ≈ 1.2*C(n), i.e., we’re seeing exponential growth with C(n) = C(0)*(1.2)^n. Note that he has the advantage that he can just “zoom out” to redraw the scale of the y-axis.
After that initial segment, he starts discussing some parameters relevant to the topics of our course (“E = Average number of people someone infected is exposed to each day,” and “p = Probability of each exposure becoming an infection”).
Also starting at around 1:50 mark, he shows what a logarithmic scale is, and why it’s useful for graphing exponential growth curves–they turn into straight lines on a log scale! And then he does a linear regression, and shows the R^2 (the coefficient of determination!)