conditional probability

HW7 #8 (also uses Bayes’ Rule!)

Here is a snapshot of Exercise #8 on HW7-ConditionalProbability:

The first step, as usual, is to write down the given probabilities in terms of the following events:

R = “spends time in the resource room”

“> 90” = “speends more than 90mins per week in the resource room”

Then the first two sentences tell us:

P(R) = 0.66 (and so P(not R) = 0.34)

P(> 90 | R) = 0.5

Then by the Multiplication Rule, we can compute P( > 90 ):

P(> 90) = P(> 90 | R) * P(R) = 0.5*0.66 = 0.33

(This should make sense from reading the first two sentences! If 66% of students spend time in the resource room, and half of those spend more than 90 minutes, then it should be clear that 33% of all students spend more than 90 minutes in the resource room.)

Now let’s look at what the exercise is asking us for: “If a randomly chosen student did not pass the course, what is the probability that he or she did not study in the resource room?”

We can rephrase this as “what is the probability that a randomly selected student did not study in the resource room given that the student did not pass the course?”, i.e., we need to calculate the conditional probability

P(not R | fail )

or, if we use “none” in place of “not R” (to match the label in the table), and use “F” for “fail“, we need to calculate:

P(not R | F)

We can do this using Bayes’ Theorem! Recall that Bayes’ Theorem gives us a way of calculating conditional probability:

Applying this to P(not R | fail) gives us:

P(none | F) = P(F | none)*P(none) / P(F)

We can calculate the numerator as follows:

P(F | none) = 0.69 (since from the table, 31% of those those students who do not use the resource room pass)

and so

P(F | none)*P(none) = 0.69*0.34

But for the denominator P(F) we need to overall percentage of students who fail, which is not immediately given in the table. We need to calculate this by accounting for the students who fail in the three different categories (events) given in the table:

the 69% of “none” students who fail, i.e., P(F | none) = 0.69
the 54% of “1-90” students who fail, i.e., P(F | 1-90) = 0.54
the 33% of “>90” students who fail, i.e., P(F | >90) = 0.33

We need to multiply each of these by the percentages of students in each category:

34% of the students are in the “none” category, i.e., P(none) = 0.34
33% of the students are in the “1-90” category, i.e., P(1-90) = 0.33
33% of the students are in the “>90” category, i.e., P(>90) = 0.33

Then:

P(F) = P(F | none)*P(none) + P(F | 1-90)*P(1-90) + P(F | >90)*P(>90)

= (0.69)(0.34) + (0.54)(0.33) + (0.33)(0.33)

Thus, the solution is

P(none | F) = [0.69*0.34] / [(0.69)(0.34)+(0.54)(0.33)+(0.33)(0.33)]

Note: I will post a snapshot of a tree diagram for this exercise that may help visualize these calculations!

I will also post a note about “The Law of Total Probability” which is behind the P(F) calculation above!

An Introduction to Bayes Theorem (including videos!)

We needed to use Bayes’ Theorem to solve HW7 #2. In this post, I try to briefly address the following questions:

What is Bayes’ Theorem?
Where does it come from?
What is the “Bayesian interpretation” of probability?
Why is called “Bayes'” Theorem?

Also, at the bottom of the post are a handful of videos regarding Bayes Theorem (including applications to medical testing!), and links to a couple books entirely about Bayesian probability.

What is Bayes’ Theorem?

Bayes’ Theorem (or Bayes’ Rule) is following formula for computing conditional probability (screenshot taken from https://en.wikipedia.org/wiki/Bayes%27_theorem#Statement_of_theorem):

Where does Bayes’ Theorem come from?

Where does formula above for P(A | B) come from? We just have to do some algebra on the definition of conditional probability.

Start with the definition of conditional probability, applied to P(A | B) and P(B | A):

P(A | B) = P(A & B)/P(B)

P(B | A) = P(A & B)/P(A)

Now “clear the denominators” on the RHS of each equation by multiplying thru by P(B) and P(A), respectively:

P(A | B) * P(B) = P(A & B)

P(B | A) * P(A) = P(A & B)

Since the RHS is in both these equations, we know the two LHS of the equations are equal to each other!

P(A | B) = P(B | A) * P(A)/P(B)

Now just divide through by P(B) and we get Bayes’ Rule:

P(A | B) * P(B) = P(B | A) * P(A)

What is the “Bayesian interpretation” of probability?

Also from the wikipedia entry for Bayes’ Theorem

See the wikipedia entry for Bayesian probability for more on this!

Why is it called Bayes’ Rule?

One more quote from the wikipedia entry for Bayes’ Theorem:

Bayes’ theorem is named after Reverend Thomas Bayes (/beɪz/; 1701?–1761), who first used conditional probability to provide an algorithm (his Proposition 9) that uses evidence to calculate limits on an unknown parameter, published as An Essay towards solving a Problem in the Doctrine of Chances (1763). In what he called a scholium, Bayes extended his algorithm to any unknown prior cause. Independently of Bayes, Pierre-Simon Laplace in 1774, and later in his 1812 Théorie analytique des probabilités, used conditional probability to formulate the relation of an updated posterior probability from a prior probability, given evidence. Sir Harold Jeffreys put Bayes’s algorithm and Laplace’s formulation on an axiomatic basis. Jeffreys wrote that Bayes’ theorem “is to the theory of probability what the Pythagorean theorem is to geometry.”

Videos on Bayes Theorem:

Here are two introductions to Bayes Theorem:

An important application of Bayes Theorem is accuracy of medical tests–this is very timely since there is a lot of discussion about the accuracy of coronavirus testing! Here are two videos specifically on that topic:

Textbooks on Bayesian :

If you want to go even further, there are entire books devoted to Bayesian probability/statistics. Here are two introductory textbooks that look interesting (in fact, I hope to read them myself at some point!):

“Bayes’ Rule: A Tutorial Introduction to Bayesian Analysis”
- in particular, see here for a pdf of Ch 1, which goes through a handful of example applications
“Bayesian Statistics the Fun Way: Understanding Statistics and Probability with Star Wars, LEGO, and Rubber Ducks”
- you could try reading Ch 7, which is available as a pdf, and which is titled “Bayes’ Theorem with LEGO”!

HW7 #2 (using Bayes’ Rule)

Here is a snapshot of Exercise #2 on HW7-ConditionalProbability:

The first step with this exercise is to write down the given probabilities in terms of events that we can call:

W = neighbor waters the plant

D = plant dies

So we are given the following in the statement of the problem:

P( D | W ) = 0.5 (and so P( not D | W ) = 1 – 0.5 = 0.5)

P( D | not W ) = 0.85 (and so P( not D | W ) = 1 – 0.85 = 0.15)

Also we are given P(W) = 0.83 (and so P(not W) = 1 – 0.83 = 0.17)

We can arrange these into a tree diagram, and also use the Multiplication Rule along the branches of the tree to compute the “joint probabilities”:

P(W & D) = P(W) * P(D | W) = (0.83)(0.5) = 0.415

P(W & not D) = P(W) * P(not D | W) = (0.83)(0.5) = 0.415

P(not W & D) = P(not W) * P(D | not W) = (0.17)(0.85) = 0.1445

P(not W & not D) = P(not W) * P(not D | not W) = (0.17)(0.15) = 0.0255

(Note that these four add up to 1, as they should, since these 4 combinations cover the 4 possible outcomes! You can think of this as a probability distribution over these 4 possible outcomes.)

A tricky part of this question is interpreting what probability the question is asking for. It turns out that “What is the probability that the plant died because neighbor forgot to water it?” corresponds to P(not W | D)!

In order to compute this probability from the given probabilities, we need to apply what’s called Bayes’ Theorem, which comes from the definition of conditional probability.

(See this post for a longer introduction to Bayes’ Theorem, including its algebraic derivation from the definition of conditional probability.)

Here is a statement of Bayes’ Theorem, taken from https://en.wikipedia.org/wiki/Bayes%27_theorem#Statement_of_theorem:

We can apply Bayes’ Theorem this to compute P(not W | D); here is the tree diagram and the calculation of P(not W | D) (in the bottom left part of the page):

WebWork Hints: Conditional Probability (HW6 & HW7)

Here are recaps of the WebWork exercises we went over in the Blackboard Collaborate class session earlier today (remember that you can view the recording of the BB Collaborate session at https://us-lti.bbcollab.com/recording/dda6c10a1bf645ac99623a8f9549af40).

(If you catch any errors in my solutions below, please let me know!)

HW6:

#16: We went over #16 first–it helps to understand these tree diagrams before doing #15 (below).

Here’s the tree diagram from#16 (the probabilities on your tree may be different):

As we discussed, the tree diagram shows various probabilities for a certain probability experiment, which you can think of as two sequential coin flips:

the first coin flip comes up as A or B, with probabilities 0.7 and 0.3, respectively (think of this as a weighted coin!)
the second coin flip comes up as C or D–but the probabilities depend on whether the first coin flip came up A or B!
- in particular, the conditional probability P(C|A) means the probability of C given that A has occurred, i.e., P(C|A) is the number attached to the branch that leads to C from A. Thus, in this example, P(C|A) = 0.45.
- Similarly, you can read off P(D|A), P(C|B) and P(D|B) directly from the tree diagram: 0.55, 0.2, and 0.8 respectively.
- You can compute probabilities such P(A∩C) and P(B∩D) by using the Multiplication Rule. If we write it out for P(A∩C):
  - P $P (A \cap C) =$
- Finally, to compute P(C), add up the probabilities of the two different paths that lead to the outcome C, i.e., via A or via B:
  - P(C) = P $P (A \cap C) =$ P $P (A \cap C) =$ $P (A \cap C) =$

#15:

Note the hint at the bottom: draw a tree diagram, like the one we saw in #16!

The probability experiment here involves choosing a randomly selected person over 40. But if you look at the questions you’re asked in (a), (b), (c), we can interpret the two “coin flips” upon selecting a person as

(1) does that person have diabetes or not; and

(2) is that person diagnosed as having diabetes or not (we can call these two outcomes as “testing positive” or “testing negative”)

Here’s a snapshot of the tree diagram I drew, with probabilities pulled from the percentages given in the statement of the exercise:

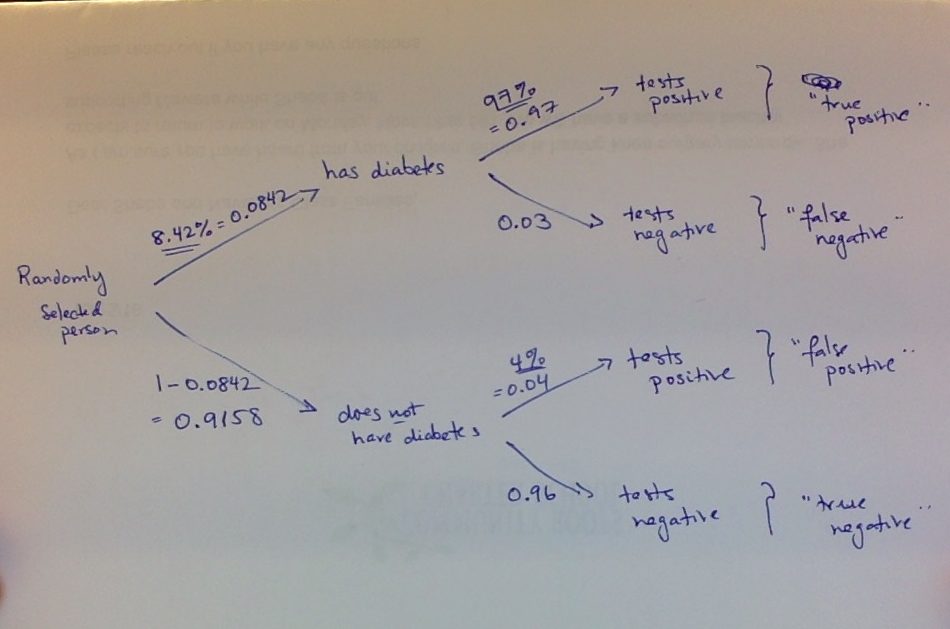
Note that I got the underlined percentages/probabilities directly from the statement of the exercise, and calculated the other ones by subtraction from 1 (e.g., we are told that 8.42% of Americans have diabetes, so 100% – 8.42% = 91.58% do not have diabetes. These are the two probabilities shown on the “first branch”–whether the randomly selected person has diabetes or not.)

Now we can just calculate the answers from this tree (as we did for #16):

a) the probability of a false positive, i.e., P( “does not have diabetes” & “tests positive”) is the product of the probabilities along that branch:

P( “does not have diabetes” & “tests positive”)= (0.9158)(0.04)

b) To find the probability that a randomly selected adult of $40$ is diagnosed as not having diabetes, i.e., P(“tests negative”), we need to add together the probabilities of travelling along the two paths that lead to that outcome (i.e., (1) has diabetes & tests negative + (2) does not have diabetes & tests negative):

P(“tests negative”) = P(“has diabetes” & “tests negative”) + P(“does not have diabetes” & “tests negative”) = (0.9158)(0.96) + (0.0842)(0.03)

[you should see how these numbers come from following the paths!]

(c) is trickier: note that the words “given that” mean we have to calculate the following conditional probability: P(“has diabetes” | “tests negative”)

By the definition of conditional probability:

P(“has diabetes” | “tests negative”) =

P(“has diabetes” & “tests negative”) / P(“tests negative”)

We get the numerator from multiplying the probabilities along that path:

P(“has diabetes” & “tests negative”) = (0.0842)(0.03)

and we already calculated the denominator in (b)!

P(“has diabetes” | “tests negative”) =

P(“has diabetes” & “tests negative”) / P(“tests negative”) =

(0.0842)(0.03)/[(0.9158)(0.96) + (0.0842)(0.03)]

HW7:

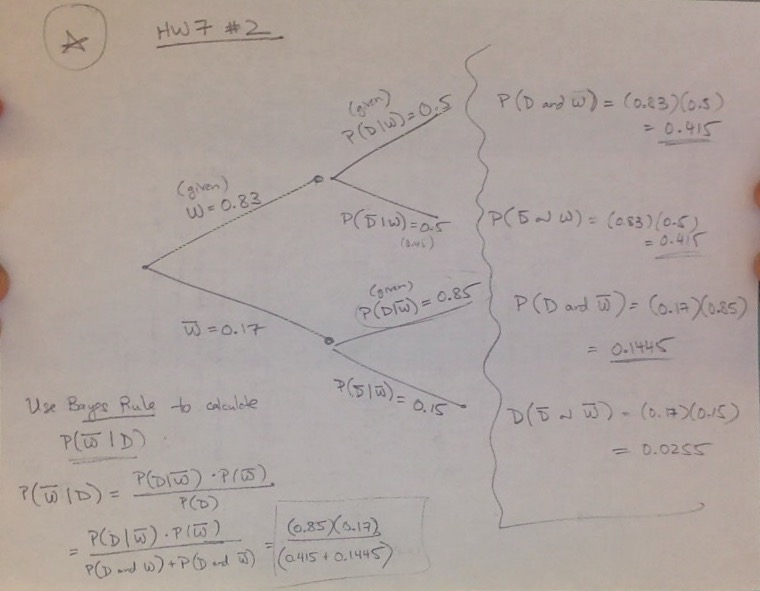
#1: This is similar to #16 from HW6! See the solutions above.

#3: The statement of the exercise reads: “Two cards are drawn from a regular deck of 52 cards, without replacement. What is the probability that the first card is an ace of clubs and the second is black?”

This is an application of conditional probability and the Multiplication Rule. First, recall that “without replacement” means that after drawing the 1st card, you don’t put it back it in the deck–so you’re sample space for the 2nd draw is reduced to 51 cards.

We need to calculate the probability

P( “1st card is ace of clubs” & “2nd card black”) =

P(“1st card ace of clubs”) * P(“2nd card black”| “1st card is ace of clubs”) =

(1/52)*(25/51)

Note that the P(“2nd card black”| “1st card is ace of clubs”) = 25/51 because the sample space is reduced to the remaining 51 cards, and of those only 25 are black (b/c we are assuming the 1st card drawn was the ace of clubs, which is black).

Also note that we can do a rough estimation of this probability, as follows:

1/52 ≈ 0.02 (actually slightly less than 0.02, since 1/50 = 0.02) and

25/51 ≈ 1/2 (actually slightly less than 1/2, since 25/50 = 1/2)

so (1/52)*(25/51) ≈ 0.02*(1/2) = 0.01

So we can estimate that the probability of drawing an ace of clubs and then a black card is less than 0.01, i.e., less than 1%.

(Using a calculator, the exact value is

(1/52)*(25/51) = 25/(52*51) = 0.00942684766214178, i.e., 0.942.. %)

#6: My statement of the exercise reads “Of 380 male and 220 female employees at the Flagstaff Mall, 250 of the men and 130 of the women are on flex-time (flexible working hours). Given that an employee selected at random from this group is on flex-time, what is the probability that the employee is a woman? ”

This is a straightforward conditional probability calcuation; you are being asked to calculate P(“woman”|”flex-time”); the “reduced sample space” for calculating this conditional probability is the number of flex-time employees, which in this example is 250+130 = 380. The number of women in this reduced sample space is 130 (the number of women on flex-time).

Hence,

P(“woman”|”flex-time”) = 130/280 = 13/28.

If you want to apply the formula for conditional probability, you can get to the solution that way. Actually it is instructive to see how that works:

P(“woman”|”flex-time”) = P(“woman” & “flex-time”)/P(“flex-time”) = (130/600)/(280/600) = (130/600)*(600/280) = 130/280.

Note that the probabilities here are relative to the original sample space of 380+220 = 600 total employees, which is why that is in the denominators for P(“woman” & “flex-time”) and P(“flex-time”); but when we do the division, those terms cancel out!

#7: You are given the values of P(E∩F), P(E|F) and P(F|E). To calculate P(E) and P(F) from these values, recall the formula for the conditional probabilities:

(1) P(E|F) = P(E∩F)/P(F)

(2) P(F|E) = P(E∩F)/P(E)

If you solve these equations for P(F) and P(E) respectively, you get:

(1a) P(F) = P(E∩F)/P(E|F)

(2a) P(E) = P(E∩F)/P(E|F)

[You should understand the algebra for getting from (1) to (1a), and from (2) to (2a)! It’s pretty simple algebra–it’s just solving x = y/z for z, i.e., z = y/x.]

Now you can use (1a) and (2a) to calculate P(F) and P(E).

Then you can solve for P(E∪F) using the Addition Rule:

P(E∪F) = P(E) + P(F) – P(E∩F)

Videos/Notes for Monday April 6: Conditional Probability

Wee below for some videos and notes recapping our Monday April 6 class session:

We started with an example of conditional probability that introduces the concept of “independent events”; see the “Introduction to Conditional Probability” video we discussed last time, starting at 9:30:

We then reviewed the class outline on Conditional Probability, in particular the 2nd page which introduces the Multiplication Rule for probabilities and the concept of independent vs dependent events
We went over some of the exercises in HW6 and HW7 that use the Multiplication Rule
You can go on to view and discuss the subsequent jbstatistics video, “Independent Events”:

This past Monday, we introduced conditional probability in our Blackboard Collaborate session. Here is a brief recap, with some online resources included below that go over the definition and go through some examples.

The conditional probability of A given B is defined as:

P(A|B) = P(A & B)/P(B)

Note that by switching A and B, we can also look at the conditional probability of B given A:

P(B|A) = P(A & B)/P(A)

(Note that the numerator is the same in both cases, since P(A&B) = P(B&A). The denominator is the probability of the “condition” i.e., the event after the vertical line “|”.)

The following 2 videos may be helpful:

If you have a copy of the textbook (Ross), you should read the examples listed on the class outline pdf. I will try to update this post with some additional online examples shortly.

Tag: conditional probability

HW7 #8 (also uses Bayes’ Rule!)

An Introduction to Bayes Theorem (including videos!)

HW7 #2 (using Bayes’ Rule)

WebWork Hints: Conditional Probability (HW6 & HW7)

Videos/Notes for Monday April 6: Conditional Probability

Conditional Probability

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons