I received a couple questions about HW6 exercises earlier this week; I thought it might be helpful to post my solutions below. Even if you have already completed these exercises, it might be worth your time to read my solutions, to see how I set up the problem and how I write out the solution.
I will update this post with some hints to the last couple exercises on HW6, since I see that many of you have completed all but the last couple exercises.
I will also start writing up some hints to the HW7 exercises shortly. Check back here for an update.
PS: Please feel free to e-mail me homework questions like this!
Someone in the class e-mailed me the following screenshot of their HW6, Problem 2:
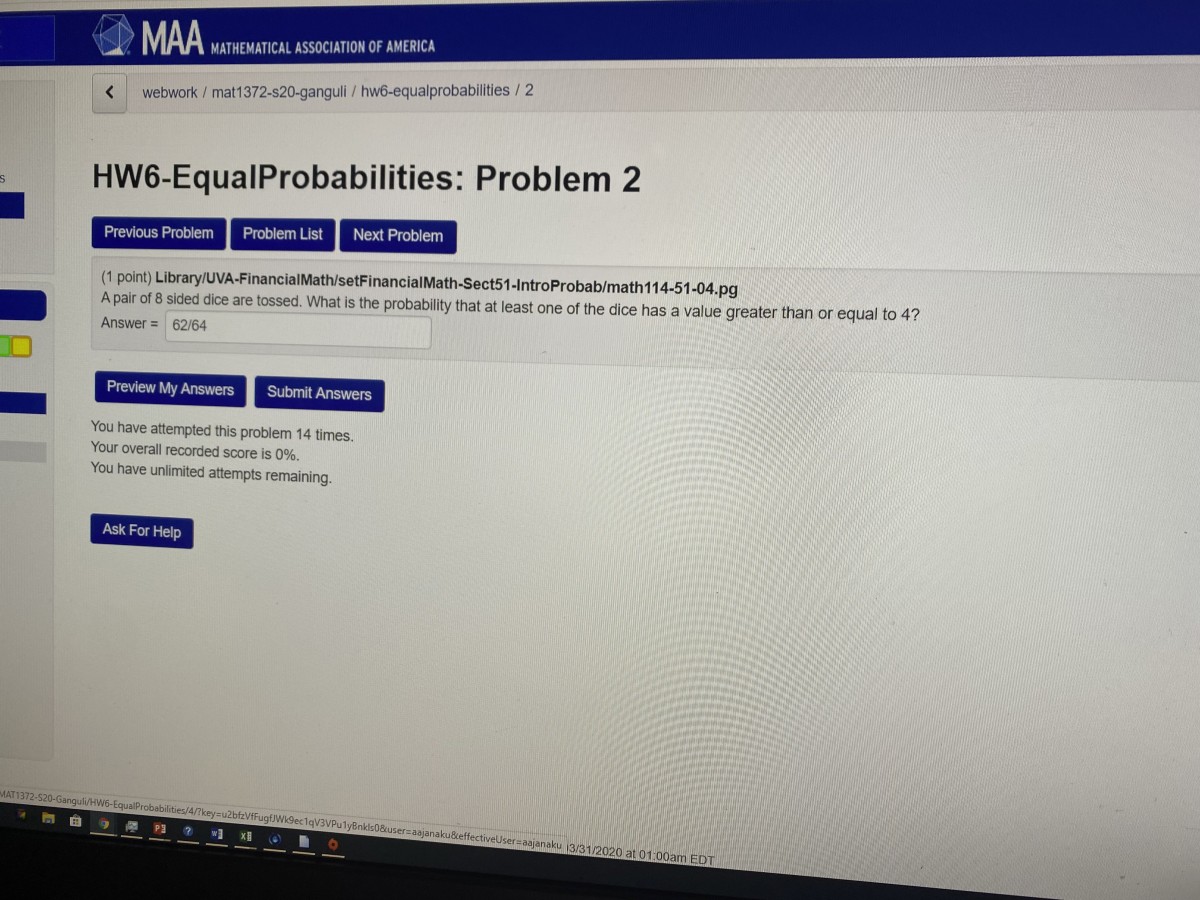
Here is my solution:

Here is a screenshot of HW6, Problem 8:
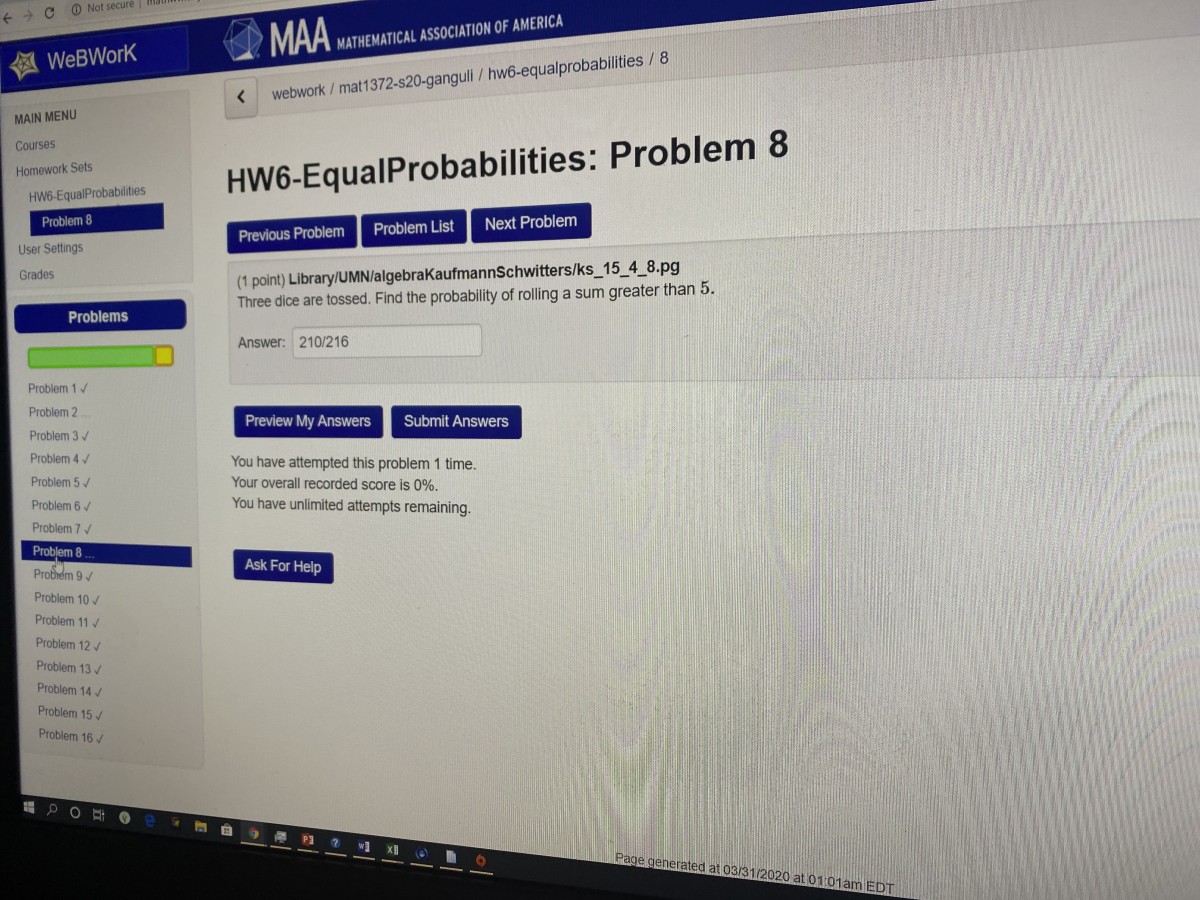
with my solution:

Here is a screenshot of HW6, Problem 6:
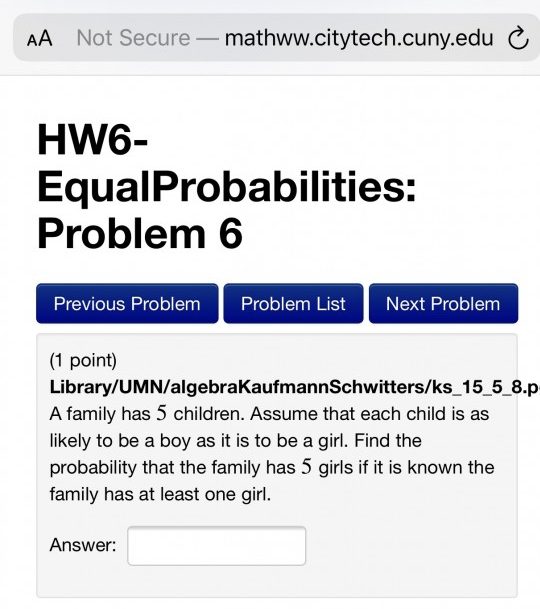
First let’s think about the sample space for a family with 5 children–what are the different gender possibilities? (Taking into account birth order!)
This is basically the same as a previous type of probability experiment we’ve discussed–flipping a coin 5 times! We have 2^5 = 32 possible outcomes in the sample space:
S = { GGGGG, GGGGB, GGGBG, …. , BBBBB}
Each of these is equally likely, but additionally we are told that we know the family has at least one girl. Hence we can rule out “BBBBB” (5 boys), and so the “reduced” sample space has 31 possibilities.
Hence, the probability of 5 girls is 1/31 (since there is obviously only one outcome with 5 girls: “GGGGG”).
Note that we can frame this as a conditional probability! We have calculated
P( GGGGG | at least one girl )



