Final Exam Review is posted

Posted on May 12, 2015 by Jonas Reitz | Leave a comment

Hi everyone,

The review sheet for the final exam is posted on the Handouts page.

Best,
Prof. Reitz

Exam 3 Review – Problem 2 STEP BY STEP (Taylor Series)

Posted on May 9, 2015 by Jonas Reitz | 1 comment

Hi everyone – here is a step-by-step solution to Problem 2 from the Exam 3 Review. If you have any questions (or notice an error), please leave a comment in reply to this post.

2. Given the differential equation $y''-xy'-y=0$ ,

a. Suppose that $y(x)$ has a Taylor series about $x=0$ , $y(x)=\sum\limits_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n=a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots$ Substitute into the differential equation and simplify by grouping together terms with similar powers of $x$ .

We start with the assumption that $y(x)= a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots$ . Find the first and second derivatives:

$y'(x)= a_1+2a_2x+3a_3x^2+4a_4x^3+\ldots$
$y''(x)= 2a_2+6a_3x+12a_4x^2+\ldots$

Now substitute $y, y'$ and $y''$ into the differential equation $y''-xy'-y=0$ :

$(2a_2+6a_3x+12a_4x^2+\ldots)-x(a_1+2a_2x+3a_3x^2+4a_4x^3+\ldots)-(a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots)=0$

Get rid of parentheses (don’t forget to distribute the $-x$ and the $-$ in front of the second and third sets of parentheses):

$2a_2+6a_3x+12a_4x^2+\ldots-a_1x-2a_2x^2-3a_3x^3-4a_4x^4-\ldots-a_0-a_1 x-a_2 x^2-a_3 x^3-a_4 x^4-\ldots=0$

Now group together by powers of $x$ :

$(2a_2-a_0)+(6a_3x-a_1x-a_1x)+(12a_4x^2-2a_2x^2-a_2x^2)+\ldots=0$

(Remember, there is more stuff hidden in the “ $\ldots$ ” – if we wanted to, we could write down more terms of $y, y'$ and $y''$ and therefore get more terms here as well).

Finally, simplify each set of parentheses and factor out $x$ :

$(2a_2-a_0)+(6a_3-2a_1)x+(12a_4-3a_2)x^2+\ldots=0$

Finally, we compare each term on the left with the corresponding term on the right – since the right side is zero, each of the expressions in the parentheses (which give the coefficients of the powers of $x$ ) must also be equal to zero:

$2a_2-a_0=0$
$6a_3-2a_1=0$
$12a_4-3a_2=0$
$\ldots$

b. Given the initial conditions $y(0)=16, y'(0)=15$ , find the first five terms of the Taylor series solution $y(x)$ .

We need to find the coefficients $a_0, a_1, a_2, a_3, a_4, \ldots$ . The first two coefficients are given by $a_0 = y(0)=16$ and $a_1 = y(1)=15$ , so we have:

$a_0 = 16$
$a_1 = 15$
$a_2 = ?$
$a_3 = ?$
$a_4 = ?$
$\ldots$

To find the remaining coefficients, we use the equations we found at the end of part a) above, and solve each one for the unknown coefficient:

$2a_2-a_0=0$ becomes $a_2 = \frac{a_0}{2}$
$6a_3-2a_1=0$ becomes $a_3 = \frac{a_1}{3}$
$12a_4-3a_2=0$ becomes $a_4 = \frac{a_2}{4}$
$\ldots$

Substituting $a_0 = 16$ into the first equation gives $a_2 = 8$ .
Substituting $a_1 = 15$ into the second equation gives $a_3 = 5$ .
Substituting $a_2=8$ into the third equation gives $a_4 = 2$ .
$\ldots$

This gives us enough coefficients to determine the first five terms of the Taylor Series. Remembering that $y(x)= a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots$ , we substitute in the values of $a_0, a_1, a_2, a_3, a_4$ to obtain:

$y(x) \approx16+15x+8x^2+5x^3+2x^4$

NOTE: Since we have only given the first five terms of the Taylor series, the resulting expression is only an approximation of $y(x)$ — in order to make it exactly equal to $y(x)$ we would need to give all infinitely many terms. This is why we replace the equals sign with the ‘wavy equals’. (Note that I also dropped the $\ldots$ at the end).

c. Use the answer to part b to obtain an approximation of $y(2)$

Here, we just substitute $x=2$ into the expression we obtained above:

$y(2) \approx16+15\cdot 2+8\cdot 2^2+5\cdot 2^3+2\cdot 2^4=150$

1 Comment

Posted in Resources

Tagged exam 3 review, problem 2, step-by-step, Taylor Series

Laplace Definition “Study Guide”

Posted on May 7, 2015 by abraham | 3 comments

Laplace transformation “transform” a differential equation into an algebraic equation by changing the equation from the time domain to the frequency domain. The differential equation is packed into one or more Laplace transform equivalent forms and manipulated algebraically.

If we apply the Laplace transformation correctly we can save a lot of time and effort. Even when the complexity of the operation required are reduced significantly, it is necessary to pay attention to the parameter contained in the Laplace transformation table.

The following equation to convert an equation from the time domain to the frequency domain:

To avoid having to do this process every single time a transform table has been created. This table can be used to convert f(t) into its F(s) equivalent and can be used to bring F(s) back into f(t). The transform table has some important parameter such as the values for “s” that are valid for that specific equation. This is the domain of convergence for that equation and is very important to understand it in order to apply the Laplace transform correctly.

Importance of the “s” value: “s>0” and “s>a”

In the following example we can see the reason for the restriction: “s > 0”. When we evaluate the integral for “s > 0” the integral converges to 1/s, but when we plug-in zero, the integral diverges and we have no solution for the integral.

Let’s take the Laplace of 1:

Fitting the equation into the Laplace transform table:

Sometimes the given equations doesn’t seem to fit any of the forms in the transform table. To solve this problem we have to use algebraic techniques to brake the equation into parts that fit the transform table. For example:

Laplace transform in 5 steps:

1. Start with a differential equation.

The first steps is have a differential equation f (t).

2. Take Laplace transformation of both sides.

The transformation has to be taken entirely on both sides of the differential
equation. Sometimes the differential equation doesn’t match the transform table
and we have to use algebraic techniques to force it to match. For example:

separate the parts of the equation connected by addition or subtraction,
to match the table, find the values for a and/or be as required by the table:

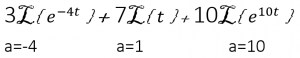
Make sure you input the “a” value correctly (check for the sign)
state the values for convergence. In this case “s > 0” since all
individual pieces of the equation converge when “s> 0”

3. Solve the resulting equation.

Once we have the equation in the frequency domain we can solve for
Laplace of y: L {y}

4. Simplify the solution.

Once we found L {y} we will proceed to reverse process done
in part 2, to match the transform table we might need to use
partial fractions or other algebraic techniques to separate the
Solution into parts that match the table.
As in step 2 watch carefully for the values of “a “and/or “s”

Example:

5. Take the inverse Laplace.

Once the solution is simplified we take inverse Laplace to bring
the equation back to time domain.

a pdf copy of this document available here: Laplace transformation

3 Comments

Posted in Uncategorized

Exam 3 Review – CORRECTIONS

Posted on May 6, 2015 by Jonas Reitz | 1 comment

Hi everyone,

I’ve updated the answer to Problem 1b on the Exam #3 Review. It should be:

1b. $I(t)=-234.261e^{-15t}\sin(32.0156t)$

NOTE: The term involving cosine disappears because the coefficient turns out to be zero – although, based on the number of decimals you used, you may have a number very close to zero instead (rounding error).

Regards,
Prof. Reitz

1 Comment

Posted in Uncategorized

Tagged corrections, exam 3 review

WeBWorK 12-day grace period

Posted on May 5, 2015 by Jonas Reitz | Leave a comment

Hi everyone,

I have re-opened all of your past WeBWorK assignments (except Assignment 16, which is due on Tuesday) to give you the opportunity to complete any unfinished problems. They will close again on Sunday, May 17th, at midnight.

This is a pretty seriously awesome opportunity to improve your score in the class.

Remember, completing 80% of all WeBWorK problems gives you full credit for webwork – anything more than that is extra credit.

Happy WeBWorKing,
Prof. Reitz

Euler’s Method

Posted on May 4, 2015 by d.Santos | 1 comment

When given a first order differential equation, we may use the various types of strategies that we earned such as exact, linear, separable, etc. Sometimes these strategies do not help us solve the equation meaning we can’t find an explicit solution (can’t find y=…). This is where Euler’s method comes into play. Euler’s method helps us find an approximation for the solution of a differential equation by generating a series of points. . The foundation for Euler’s Method is to use the concept of local linearity to join the multiple small line segments so that they make a close approximation to the function.

Definition of local linearity: if you zoom in (using the same zoom factor in both directions) on a point on the graph, the graph eventually appears to be a straight line whose slope is the same as the slope (derivative) of the tangent line at that point.

Euler’s Method Formula: y_n+1=y_n + h*f(t_n,y_n)

For Euler’s Method we are given useful information (“givens”) to help us find y_n. The givens are:

The differential equation y’= f(t_n,y_n)

NOTE: This helps us find the slope for the points by plugging in the points into the equation.

Initial value point y(t₀)=y₀, also written as (t_0,y_o)

NOTE: We use our initial value to find

(t_1,y₁)

(t_2,y₂)

(t_3,y₃)

(t_n,y_n)

The step size h. (optional)

NOTE: When the step size is not given, it is up to your discretion to decide whether you want a close approximation or not. Recall, in Calculus I, we learned how to find the area under the curve. The basic idea is to use smaller rectangles under that curve, so our area approximation can be close as possible to the actual area. This idea is the same for the step size, the smaller your step size is from one point to the other, the closer your approximation for the point y(t_n)= y_nwill be. Also, because of the step size we are allowed to find the values of the succeeding t’s by adding the step size to the preceding t.

Sample Problem:

Given y’= t²+3t-1, y(0)=1. Find the value of y(2).

Step 1:

We have to decide on the step size (h) to find the next series of points until we get to y(2) . A good guess for an approximation may be 0.5. It depends on how many steps you would like to use. Let’s say I want to use 5 steps. A formula to let me know what my value of h will be:

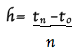where n= the steps that will be used. Let’s plug it in and see if the guess will give me a better approximation

Screen Shot 2015-05-04 at 11.10.31 AM

So, we were off by 0.1. We will use 0.4.

Step 2: Find the “t”s

We use our step size and add on to the previous t

t₁= t_o + 0.4 = 0 + 0.4 = 0.4

t₂= t₁ + 0.4 = 0.4 + 0.4 = 0.8

t₃= t₂ + 0.4 = 0.8 + 0.4 = 1.2

t₄= t₃ + 0.4 = 1.2 + 0.4 = 1.6

t₅= t₄ + 0.4 = 1.6 + 0.4 = 2

NOTE: Last Step size should be the value that are ask to find, y(2)

Step 3: Finding our slopes to find our “y”s. We use the Euler’s Method formula to find our slope first, in order to find the succeeding y. It’s like recursive sequences, we cannot proceed to the next points without the preceding data from the previous equation.

y_n+1=y_n + h*f(t_n,y_n)

What we know:

Previous “y”s
How to find the slope
h=0.4

y₁=y₀+ 0.4 x ((0)²+3(0)-1)= 1+0.4(-1)=0.6

y₂=y₁+ 0.4 x ((0.4)²+3(0.4)-1)= 0.6+0.4(0.36)=0.744

y₃=y₂+ 0.4 x ((0.8)²+3(0.8)-1)= 0.744+0.4(2.04)=1.56

y₄=y₃+ 0.4 x ((1.2)²+3(1.2)-1)= 1.56+0.4(4.04)=3.176

y₅=y₄+ 0.4 x ((1.6)²+3(1.6)-1)= 3.176+0.4(6.36)=5.72

A table is also helpful when finding the solution.

Subscript	t	y	y’
0	0	1	(0)²+3(0)-1=-1
1	0.4	0.6	(0.4)²+3(0.4)-1
2	0.8	0.744	(0.8)²+3(0.8)-1
3	1.2	1.56	(1.2)²+3(1.2)-1
4	1.6	3.176	(1.6)²+3(1.6)-1
5	2	5.72	(2)²+3(2)-1

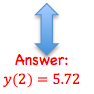
Screen Shot 2015-05-04 at 11.15.04 AM

Note: You can also see a visual of Euler’s Method (graphically) using graphic software. The graph below is from www.mathscoop.com

Screen Shot 2015-05-04 at 11.16.35 AM

Here is another great example:

1 Comment

Posted in Uncategorized

Partial Fractions: What if the top has a higher power than the bottom?

Posted on May 1, 2015 by Jonas Reitz | 2 comments

Partial fractions decomposition only works when the numerator has a smaller degree than the denominator. For example, here:

$\frac{s^2-s-9}{s-4}$

the numerator has degree 2 (because of the s-squared), and the denominator has degree 1, so partial fractions won’t work. What do we do? We need to divide the top by the bottom, using polynomial long division (this is another trick you may or may not remember from Algebra). When we are done, we get:

$\frac{s^2-s-9}{s-4} = s+3+\frac{3}{s-4}$

and we can proceed to take the Inverse Laplace Transform of the expression on the right.

To see how long division works for polynomials, check out these videos:

Basic examples:

Another example:

Best of luck – write back if you get stuck.
-Prof. Reitz

2 Comments

Posted in Resources

Tagged improper fractions, partial fractions, polynomial long division

Exam 3 Review is posted

Posted on May 1, 2015 by Jonas Reitz | Leave a comment

Hi everyone,

The review sheet for Exam #3 is posted on the Handouts page.

NOTE: You will be provided with a two-page formula sheet for use on the exam. This formula sheet appears on pages 2-3 of the Exam 3 Review. The final page of the Review contains the solutions.

Let me know if you have any questions.

Regards,
Prof. Reitz

Repeated Roots Second Order Linear Homogeneous Equation

Posted on May 1, 2015 by Carolina | 4 comments

Overview

Second order linear equations become homogeneous when the linear function of y and y’ (which can be written in the form y” + p(t)y’ + q(t)y = g(t)) is equal to zero. In other words when g(t)=0.

This guide will be discussing how to solve homogeneous linear second order differential equation with constant coefficient, which is written in the following form:

y”+by’+cy = 0

The first step is to use the equation above to turn the differential equation into a characteristic equation. The characteristic equation is written in the following form:

r² +br+c = 0

Second to find the roots, or r₁and r₂you can either factor or use the quadratic formula:

r² = ± -b √b²-4ac

It is important to remember when to the particular equation above. There will problems where the variable a is not needed in the quadratic formula because there will be no a in the differential equation. In the cases where there is no a variable limit the a variable from the quadratic equation. The quadratic equation will the look like the following:

r² = ± -b √b²-4c

Once you get repeated roots , or r₁ and r₂ from the characteristic equation then y = e^rt is considered a solution of the differential equation.

The next step would be to plug r₁ and r₂ into the general equation:

y = C₁ e^r1t +C₂ e^r2t

Another important thing to realize and remember is that when solving a homogeneous equation for a repeated root the solution will end up cancelling out. In order to avoid this a “t” needs to be place in the general solution. The general solution for the repeated root will then be in the following form:

y = C₁ e^r1t +C₂t e^r2t

Sample Problem

Problem 1:

y”+12y’+36 = 0

Step 1: Turn the differential equation into a characteristic equation

r² + br + c = 0

r² + 12r + 36 = 0

Step 2: Factor the characteristic equation

r² + 12r + 36 = 0

(r + 6) (r + 6) = 0

r₁ = -6 r₂ = -6

Step 3: Use y = e^rt as a solution for r₁ and r₂

y = e^rt

y = e^-6t

Step 4: Plug r₁ and r₂ into the general solution for the repeated roots

y = C₁ e^r1t +C₂t e^r2t

y = e^rt

y = e^-4t

Step 4: Plug r₁ and r₂ into the general solution for the repeated roots

y = C₁ e^r1t +C₂t e^r2t

y = C₁ e^-4t +C₂t e^-4t

y = C₁ e^-6t +C₂t e^-6t

Problem 2:

y”+8y’+16 = 0 , y(0) = 2 y’(0)= 6

Step 1: Turn the differential equation into a characteristic equation

r² + br + c = 0

r² + 8r + 16 = 0

Step 2: Factor the characteristic equation

r² + 8r + 16 = 0

(r + 4) (r + 4) = 0

r₁ = -4 r₂ = -4

Step 3: Use y = e^rt as a solution for r₁ and r₂

y = e^rt

y = e^-4t

Step 4: Plug r₁ and r₂ into the general solution for the repeated roots

y = C₁ e^r1t +C₂t e^r2t

y = C₁ e^-4t +C₂t e^-4t

The following three videos are form Khan Academy. I find these videos ever useful . I would recommend you watch them if you are still confused about Repeated Roots of Second order linear homogeneous equation.

4 Comments

Posted in Study Guide, Uncategorized

Tagged characteristic equation, differential equations, khan academy

Non-homogeneous Second Order Differential Equations Using Methods Of Undetermined Coefficients

Posted on May 1, 2015 by shawn chowdhury | 1 comment

Non-homogeneous differential equations are the same as homogeneous differential equations, However they can have terms involving only x, (and constants) on the right side. The interesting part of solving non homogeneous equations is having to guess your way through some parts of the solution process.
You also can write non-homogeneous differential equations in this format: y” + p(x)y’ + q(x)y = g(x).

The Reason I’ve chosen this problem is because it basically touches every aspect of a Non-homogeneous second order differential Equation using methods of undetermined coefficients.

y” + 6y’ + 9y = -578 sin 5t

The first step when dealing with undetermined or constant coefficients is getting the Characteristic equation. Which will later become the first half of our solution.

y” + 6y’ + 9y = 0
r^2 + 6r + 9 = 0
( r+3 ) ( r+3) = 0
R1 = -3 R2 = -3

When solving the characteristic equation sometimes we run into repeated roots. In this case we must use the following formula y = C1e^r1(t)+C2 (t)e^r2(t)

y (t) = C1e^-3t + C2te^-3t

After finding the characteristic equation our next step in this linear equation is to guess the y. In this case our y is going to include both sin and cosine. We make this guess because the cosine is going to come up eventually when finding the derivative and by adding it into the equation, it will allow us to cancel it out later on throughout the steps in the solution process. We also will need to find the y’ and y”.

y = C sin (5t) + D cos (5t)
y’ = 5 C cos (5t) – 5 D sin (5t)
y” = -25 C sin (5t) + 9 D cos (5t)

Now we plug it back into its original equation.

-25 C sin (5t) – 25 D cos (5t)
+30 C cos (5t) – 30 D sin (5t)
+9 C sin (5t) + 9 D sin (5t)
= -578 sin 5(t)

At this point we want to cancel and group any like terms.

(-16C -30D) sin (5t) + (-16D + 30C) cos (5t) = -578 sin (5t)

Resulting two equations.

(-16) (C) – (30) (D) = -578
(30) (C) – (16) (D) = 0
Now we must find Find C & D
(30) (C) – (16) (D) = 0
+16 (D) +16 (D)
C = (16/30) (D)

Now we plug in C back into the next equation.

(-16)(16/30D) – (30) (D) = -578
(-256/30)(D) – (30) (D) = -578
(-578/15)D = -578
D = 15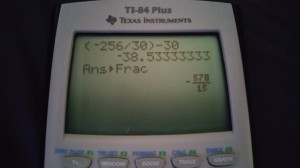

When calculating the (-256/30)(D) – (30) (D).
We use the calculator to find the fraction value by entering math > frac > enter.
Plug in D

C = (16/30) (D)
C = (16/30) (15)
C = 8

After finding all values we’re finally ready to plug in all variables and combine the homogeneous equation with its general solution.
Resulting in:
y (t) = C1e^-3(t) + C2(t)e^-3(t) + 8 sin 5(t) + 15 cos 5(t)
If we were given the case of finding a particular solution, we will have to take this a few steps further to and plug in the (t) value. But fortunately for us this general solution will suffice.

Below I have included videos that has helped me understand how to solve Non-homogeneous second order differential Equations using methods of undetermined coefficients. Khan academy has been an incredible help in the understanding of all things in relation to differential equations.

Problem listed above was taken from the midterm review, question 9 by Professor JReitz.

1 Comment

Posted in Study Guide

Tagged characteristic equation, differential equations, Non-homogeneous

MAT 2680 Differential Equations

Final Exam Review is posted

Exam 3 Review – Problem 2 STEP BY STEP (Taylor Series)

Laplace Definition “Study Guide”

Importance of the “s” value: “s>0” and “s>a”

Fitting the equation into the Laplace transform table:

Laplace transform in 5 steps:

1. Start with a differential equation.

2. Take Laplace transformation of both sides.

3. Solve the resulting equation.

4. Simplify the solution.

5. Take the inverse Laplace.

Exam 3 Review – CORRECTIONS

WeBWorK 12-day grace period

Euler’s Method

Partial Fractions: What if the top has a higher power than the bottom?

Exam 3 Review is posted

Repeated Roots Second Order Linear Homogeneous Equation

Non-homogeneous Second Order Differential Equations Using Methods Of Undetermined Coefficients

Related sites:

Handy Web Resources

Math StackExchange

Recent Posts

Recent Comments

Categories

Archives

Meta

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons

Importance of the “s” value: “s>0” and “s>a”

Fitting the equation into the Laplace transform table:

Laplace transform in 5 steps:

1. Start with a differential equation.

2. Take Laplace transformation of both sides.

3. Solve the resulting equation.

4. Simplify the solution.

5. Take the inverse Laplace.

Related sites:

Handy Web Resources

Recent Posts

Recent Comments

Categories

Archives

Meta

Tags

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright