Author Archives: Jonas Reitz

Final Grades are posted

Posted on May 26, 2015 | Leave a comment

Hi everyone,

Final grades for the course have been submitted to CUNYFirst, and a detailed breakdown of your grade (including your final exam score, your “Study Guide” project score, and so on) can be found on the GRADES page.

I wish you the very best in your future endeavors – it was a pleasure working with you this semester.

Best regards,
Prof. Reitz

Leave a comment

Posted in Resources

Tagged , ,

Final Exam Review CORRECTION

Posted on May 17, 2015 | 2 comments

Hi everyone,

I’ve updated the answer to problem #14 – the correct answer is:

Q(t)=1.31317e^{-4t}\sin(7.31057t)+2.4e^{-4t}\cos(7.31057t)

 

I(t)=-22.798e^{-4t}\sin(7.31057t)

 

Best,
Prof. Reitz

2 Comments

Posted in Resources

Tagged ,

Exam 3 Grades are posted, and SPECIAL OFFER

Posted on May 16, 2015 | Leave a comment

Hi everyone,

The grades for Exam 3 are posted on the Grades page (email me if you have forgotten the password).

This exam covered a great deal of material and, while overall grades were comparable to the first exam, I’m sure not everyone did as well as they would have liked.  You may improve your score on the exam by completing the Special Offer below.

Let me know if you have any questions, and best of luck with your studying!
Prof. Reitz

Exam 3 Special Offer – earn bonus points.  You can improve your grade on the exam, by doing the following:

  1. Choose ONLY ONE problem in which you did NOT earn full points.  You are working to earn back (some of ) the points you missed on this problem.
  2. Do the problem over, neatly and completely, start to finish, on a separate sheet of paper.
    1. Don’t forget your name, the date, and the problem number.
  3. On the same sheet, write a short statement (one or two complete sentences) explaining your mistake(s) – the purpose is to let me know that you understand what you did wrong.
  4. Hand in your original exam and your corrected problem and explanation, stapled together, in class on Thursday (the day of the final exam).
  5. Bonus points will be added to your Exam 3 score based on the number of points you missed on the chosen problem,  the accuracy of your corrections and explanation, and your overall grade on the exam.  Bonus points are limited as follows:
    1. If you received less than 60% on the exam, you can earn a maximum of 20 bonus points.
    2. If you received between 60% – 69% on the exam, you can earn a maximum of 15 bonus points.
    3. If you received between 70% – 79% on the exam, you can earn a maximum of 10 bonus points.
    4. If you received between 80% – 89% on the exam, you can earn a maximum of 5 bonus points.
    5. If you received between 90% or more on the exam, you can earn a maximum of 2 bonus points.

 

Leave a comment

Posted in Assignments, Resources

Tagged , ,

Final Exam Review is posted

Posted on May 12, 2015 | Leave a comment

Hi everyone,

The review sheet for the final exam is posted on the Handouts page.

Best,
Prof. Reitz

Leave a comment

Posted in Resources

Tagged ,

Exam 3 Review – Problem 2 STEP BY STEP (Taylor Series)

Posted on May 9, 2015 | 1 comment

Hi everyone – here is a step-by-step solution to Problem 2 from the Exam 3 Review. If you have any questions (or notice an error), please leave a comment in reply to this post.

2.  Given the differential equation 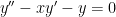y''-xy'-y=0,

a. Suppose that 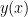y(x) has a Taylor series about 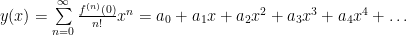x=0,y(x)=\sum\limits_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!} x^n=a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots Substitute into the differential equation and simplify by grouping together terms with similar powers of x.

We start with the assumption that 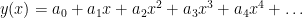y(x)= a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots.  Find the first and second derivatives:

  • y'(x)= a_1+2a_2x+3a_3x^2+4a_4x^3+\ldots
  • y''(x)= 2a_2+6a_3x+12a_4x^2+\ldots

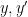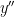Now substitute y, y' and y'' into the differential equation y''-xy'-y=0:

(2a_2+6a_3x+12a_4x^2+\ldots)-x(a_1+2a_2x+3a_3x^2+4a_4x^3+\ldots)-(a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots)=0

 

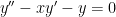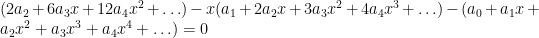
Get rid of parentheses (don’t forget to distribute the 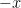-x and the - in front of the second and third sets of parentheses):

2a_2+6a_3x+12a_4x^2+\ldots-a_1x-2a_2x^2-3a_3x^3-4a_4x^4-\ldots-a_0-a_1 x-a_2 x^2-a_3 x^3-a_4 x^4-\ldots=0

 

Now group together by powers of x :

(2a_2-a_0)+(6a_3x-a_1x-a_1x)+(12a_4x^2-2a_2x^2-a_2x^2)+\ldots=0

 

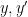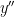(Remember, there is more stuff hidden in the “\ldots” – if we wanted to, we could write down more terms ofy, y' and y'' and therefore get more terms here as well).

Finally, simplify each set of parentheses and factor out x:

(2a_2-a_0)+(6a_3-2a_1)x+(12a_4-3a_2)x^2+\ldots=0

 

Finally, we compare each term on the left with the corresponding term on the right – since the right side is zero, each of the expressions in the parentheses (which give the coefficients of the powers of x) must also be equal to zero:

  • 2a_2-a_0=0
  • 6a_3-2a_1=0
  • 12a_4-3a_2=0
  • \ldots

b. Given the initial conditions y(0)=16, y'(0)=15, find the first five terms of the Taylor series solution y(x).

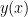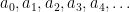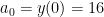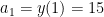We need to find the coefficients a_0, a_1, a_2, a_3, a_4, \ldots.  The first two coefficients are given by a_0 = y(0)=16 and a_1 = y(1)=15, so we have:

  • a_0 = 16
  • a_1 = 15
  • a_2 = ?
  • a_3 = ?
  • a_4 = ?
  • \ldots

To find the remaining coefficients, we use the equations we found at the end of part a) above, and solve each one for the unknown coefficient:

  • 2a_2-a_0=0 becomes a_2 = \frac{a_0}{2}
  • 6a_3-2a_1=0 becomes a_3 = \frac{a_1}{3}
  • 12a_4-3a_2=0 becomes a_4 = \frac{a_2}{4}
  • \ldots

Substituting 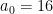a_0 = 16 into the first equation gives a_2 = 8.
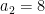Substituting 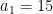a_1 = 15 into the second equation gives a_3 = 5.
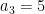Substituting 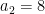a_2=8 into the third equation gives a_4 = 2.
\ldots

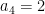This gives us enough coefficients to determine the first five terms of the Taylor Series.  Remembering that 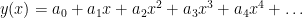y(x)= a_0+a_1 x + a_2 x^2 + a_3 x^3 + a_4 x^4 +\ldots, we substitute in the values of a_0, a_1, a_2, a_3, a_4 to obtain:

y(x) \approx16+15x+8x^2+5x^3+2x^4

 

NOTE: Since we have only given the first five terms of the Taylor series, the resulting expression is only an approximation of 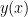y(x) — in order to make it exactly equal to 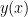y(x) we would need to give all infinitely many terms.  This is why we replace the equals sign with the ‘wavy equals’.  (Note that I also dropped the $\ldots$ at the end).

c. Use the answer to part b to obtain an approximation of y(2)

Here, we just substitute 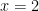x=2 into the expression we obtained above:

y(2) \approx16+15\cdot 2+8\cdot 2^2+5\cdot 2^3+2\cdot 2^4=150

 

1 Comment

Posted in Resources

Tagged , , ,

Exam 3 Review – CORRECTIONS

Posted on May 6, 2015 | 1 comment

Hi everyone,

I’ve updated the answer to Problem 1b on the Exam #3 Review.  It should be:

1b. I(t)=-234.261e^{-15t}\sin(32.0156t)

NOTE: The term involving cosine disappears because the coefficient turns out to be zero – although, based on the number of decimals you used, you may have a number very close to zero instead (rounding error).

Regards,
Prof. Reitz

1 Comment

Posted in Uncategorized

Tagged ,

WeBWorK 12-day grace period

Posted on May 5, 2015 | Leave a comment

Hi everyone,

I have re-opened all of your past WeBWorK assignments (except Assignment 16, which is due on Tuesday) to give you the opportunity to complete any unfinished problems.  They will close again on Sunday, May 17th, at midnight.

This is a pretty seriously awesome opportunity to improve your score in the class.

Remember, completing 80% of all WeBWorK problems gives you full credit for webwork – anything more than that is extra credit.

Happy WeBWorKing,
Prof. Reitz

Leave a comment

Posted in Assignments

Partial Fractions: What if the top has a higher power than the bottom?

Posted on May 1, 2015 | 2 comments

Partial fractions decomposition only works when the numerator has a smaller degree than the denominator.  For example, here:

\frac{s^2-s-9}{s-4}

the numerator has degree 2 (because of the s-squared), and the denominator has degree 1, so partial fractions won’t work. What do we do? We need to divide the top by the bottom, using polynomial long division (this is another trick you may or may not remember from Algebra).  When we are done, we get:

\frac{s^2-s-9}{s-4} = s+3+\frac{3}{s-4}

and we can proceed to take the Inverse Laplace Transform of the expression on the right.

To see how long division works for polynomials, check out these videos:

Basic examples:

Another example:

Best of luck – write back if you get stuck.
-Prof. Reitz

2 Comments

Posted in Resources

Tagged , ,

Exam 3 Review is posted

Posted on May 1, 2015 | Leave a comment

Hi everyone,

The review sheet for Exam #3 is posted on the Handouts page.

NOTE: You will be provided with a two-page formula sheet for use on the exam.  This formula sheet appears on pages 2-3 of the Exam 3 Review.  The final page of the Review contains the solutions.

Let me know if you have any questions.

Regards,
Prof. Reitz

Leave a comment

Posted in Resources

Tagged

Help with Partial Fraction Decomposition

Posted on April 23, 2015 | 43 comments

Hi everyone,

As we launch into our next topic, you will see that one of the (forgotten?) skills you will need is that of re-writing a complicated fraction as a sum of simpler fractions (“partial fraction decomposition”).  For those that need some extra help/reminder of this process, here are a couple of videos:

Partial Fraction Decomposition – a basic example.  This is a good basic example.

https://www.youtube.com/watch?v=HZTv4zCgEnA

Partial Fraction Decomposition – another example. This is a slightly longer example, and it includes a good explanation of how to set up your partial fractions for different kinds of factors in the denominator.

https://www.youtube.com/watch?v=pZ9FfGy3Cfw

 

43 Comments

Posted in Resources

Tagged , , ,