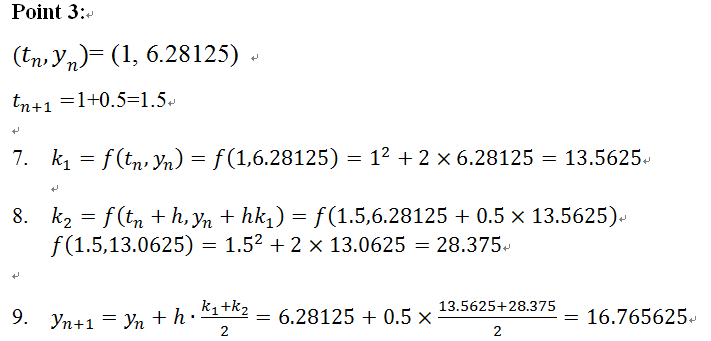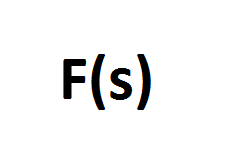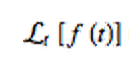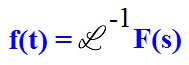Hi everyone,
Final grades for the course have been submitted to CUNYFirst, and a detailed breakdown of your grade (including your final exam score, your “Study Guide” project score, and so on) can be found on the GRADES page.
I wish you the very best in your future endeavors – it was a pleasure working with you this semester.
Best regards,
Prof. Reitz
Taylor Series are very useful for approximating function values, much more effectively than standard linear approximations.
To me Taylor Series is very easy and straight forward. There is one important thing you need to remember about Taylor series and that is
y= a0 + a1x + a2x^(2) + a3x^(3) + a4x^(4)……….+anx^(n)
y’=a1 + 2A2x +3a3x^(2) +4a4x^(3)………..
y”=2a2 + 6a3x + 12a4x^(2)…………………
and with this all you do is plug it into a the equation.
For example
y”+2y’ +y=0 y(0)=0 y’(0)=2 x=1
the first step is to find y, y’, y” which are the given above from earlier. These do not change.
Then you plug it in the formula producing
(2a2 + 6a3x + 12a4x^(2))+ 2(a1 + 2A2x +3a3x^(2) +4a4x^(3)) + (a0 + a1x + a2x^(2) + a3x^(3) + a4x^(4)) …..= 0
(2a2 + 6a3x + 12a4x^(2))+ 2a1 + 4a2x +6a3x^(2) +8a4x^(3) + (a0 + a1x + a2x^(2) + a3x^(3) + a4x^(4)) ……= 0
Now you group by the power of x.
(2a2 + 2a1 + a0) + (6a3x + 4a2x + a1x) + (12a4x^(2) + 6a3x^(2) + a2x^(2) ) + a3x^(3) + a4x^(4))….. = 0
(2a2 + 2a1 + a0) + (6a3 + 4a2 + a1)X + (12a4 + 6a3 + a2 ) x^(2) + a3x^(3) + a4x^(4))….. = 0
Now we set to equal 0
2a2 + 2a1 + a0 =0
6a3 + 4a2 + a1 = 0
12a4 + 6a3 + a2 = 0
Remember y (0) =0 and y’(0)=2
Y(0) = 0 = a0
Y’(0)= 2 = a1
Now knowing that we will plug in a0 and a1
2a2 + 2(2) + 0 =0
2a2 + 4 =0 2a2 =-4 a2 =-2
6a3 + 4(-2) + (2) = 0
6a3 -6 = 0 a3=1
12a4 + 6a3 + a2 = 0
12a4 + 6(1) + (2) = 0
12a4 + 8 = 0 a4= -(1/3)
Now you substitute a0 , a1, a2, a3, and a4 into the first equation.(note we are only doing up to the 5th term if the problem wants up to the 6th term you would find up to a5 )
y= a0 + a1x + a2x^(2) + a3x^(3) + a4x^(4)……….+anx^(n)
Producing
y= 0+ 2x – 2x^(2) + 1x^(3) – (1/3)x^(4)……….+anx^(n)
Then you plug in x in this case x = 1
y(2)= 0+ 2(1) – 2(1)^(2) + 1(1)^(3) – (1/3)(1)^(4)
y(2)= 0+ 2 – 2+ 1 – (1/3)
y(2)= – (2/3)
Posted in Uncategorized
The Laplace transform is an important technique in differential equations, and it is also widely used a lot in electrical engineering to solving linear differential equation The Laplace transform takes a function whose domain is in time and transforms it into a function of complex frequency.
The inverse Laplace transform does exactly the opposite, it takes a function whose domain is in complex frequency and gives a function defined in the time domain.
The steps to using the Laplace and inverse Laplace transform with an initial value are as follows:
1) We need to know the transformations we have to apply, which are:
L{y’}=sY(s)-y(0) L{y”}=s^2 Y(s)-sy(0)-y'(0)
2) Once we apply the proper Laplace transform to our function we then apply the initial condition
3)Then since we can’t find y(t) directly, we solve for Y(s), which is the Laplace transform of y(t)
4) Once we find Y(s), we may need to break up the equation into partial fraction form depending on the denominator. there must only be a single term in the denominator and no “s” in the numerator. (look at “Factor in Denominator” chart image attached)
5) We take the inverse Laplace transform to get y(t)
So now to apply those steps,
Let’s take for example, 2y’-y = 1 ; y(0) = 0
1) Apply the transforms. 2(sY(s)-y(0))-Y(s)= 1/s
2) Apply the initial conditions given. 2(sY(s)-0)-Y(s)= 1/s
3) Solve for Y(s). Y(s)(2s-1) = 1/s Y(s)=1/s(2s-1)
4) Apply the inverse transform. L^(-1){1/s(2s-1)} = L^(-1){1/(2s-1)-(1/s)} = e^(1/2t)-1
For another example, let’s take something that requires us to use partial fractions to get the right denominator.
F(s) = [19/(s+2)]-[1/(3s-5)]+[7/(s^5)]
So to get started on this one, we look at the Laplace transform table and see which fraction refers to the transformation. The first fraction looks like 1/(s-a) = e^(at). Although the “a” in this case would be a -2. For the second fraction, we got the same case except that the s is 3s, so all we have to do is factor out the 3, and apply the Laplace transform. And for the third fraction we see that it looks like, (n!)/s^(n+1) = t^n ; and since the exponent in the denominator is 5, the value for n = 4. But now we still have a 7 in the numerator whereas we need a 4! or 24. So to fix this all we have to do is multiply the top numerator by a constant to achieve the desired numerator, but we have to remember to divide by the same constant after taking the Laplace transform.
So it would be:
F(s) = [19/(s-(-2))]-[1/3(s-(5/3))]+[7(4!/4!)/(s^(4+1))]
So, now we have to take the inverse Laplace transform.
f(s) = 19e^(-2t) – (1/3)e^(5t/3) + 7/24(t^4)
I hope that the link to the video and images are helpful.
Posted in Uncategorized
Tagged Inverse, inverse Laplace, Laplace, Partial fraction, Transform
Several improvements to Euler’s Method exist: the backwards Euler method and the Runge-Kutta method (for Improved Euler method see BingJing Zheng’s post Improved Euler’s Method).
Backwards Euler Method with Example
Recalling that in Euler’s method, one approximates the point 
Example: Given 
Find y at t = 0
Given: At t = 0, y = 1
Find y at t = 0.5
At t = 0.5,
At t = 0.5,
At t = 0.5,
At t = 0.5,
At t = 0.5,
Find y at t = 1
At t = 1,
At t = 1,
At t = 1,
At t = 1,
At t = 1,
Runge-Kutta Method with Example
Much like the Improved Euler method, one tries to find a better fit for the definite integral of a curve. One uses the idea that a parabola would cover the most area under a curve (compared to a rectangle or trapezoid of other methods). From this idea, one found equations for the following points:
where
Example: Given
Find y at t = 0
Given: At t = 0, y = 1
Find y at t = 0.5
Find y at t = 1
Analysis
After answering the same question using both the backwards Euler method and Runge-Kutta method, one can see the accuracy of the results.
The exact solution for y(1) is 0.6321205588.
Using the Euler method, y(1) is approximately 0.375.
Using the backwards Euler method, y(1) is approximately 0.8333333333.
Using the Runge-Kutta method, y(1) is approximately 0.6328751629.
The backwards Euler method provides a better approximation than the Euler method, with a few more steps. The Runge-Kutta method provides the best approximation, but involves more calculation.
Hi everyone,
I’ve updated the answer to problem #14 – the correct answer is:
Best,
Prof. Reitz
6.2 Laplace Transform: Solution of the Initial Value Problems (Inverse Transform)
Laplace transform is used to convert a function in the t domain and transfer it to the s domain. The practical used of this transform is to solve differential equations easier. Having read the definitions and having knowledge on how the Laplace transform works we would proceed with an example in how to apply it to a differential equation with initial values.
1.Solve using Laplace Transform
y”-y’-2y=0 with the condition y(0)=1 y’=0
Step 1: Step 1 is it a differential equation? Yes, because its homogeneous and linear
Step 2: Take the Laplace from both sides L{ y”-y’-2y=0}
Step 3:Solve it algebraically
using the laplace transform chart we know f”(t)= L{f(t)-sf(0)-f'(0)
f'(t)=sL{f(t)-f(0)
Take the Laplace of the diff equation applied the initial value given :
Y(s)-s(1)-0-{sY(s)-1}-2Y(s)
Factor Y(s): Y(s)(-s-2)-s+1=0
Isolate the Y(s) : Y(s)=
therefore take -s+1 to the other side and divide from the quadric equation
Step 4: Simplify the solution by applying partial fraction
= +
= (s-2)(s+1)=A(s+1) = (s-2)(s+1)=B(s-2)
s-1= A(s+1)+B(s-2)
“”= As+A+Bs-2B
“”= As+Bs+A-2B
Combine all the letter that have s with s, and number with the terms that don’t have s on it.
A+B=1 since (1) is in front of the s we use 1 -1=A-2B
Solve the linear equations : we would solve this by using elimination method:
A-2B= -1
2A+2B=2
3A=1 therefore, A=1/3 then by substituting A into the A+B=1– (1/3)+B=1
we obtain B=2/3 and A=1/3
Finally your function is in s domain:
Reminder outline to solving differential equation using Laplace transform:
1. Start with a differential equation
4.Take the inverse Laplace transform of the solution, this would be your solution for the differential equation, at this point you should be in the t domain with a simplify equation
Important Notation:
L{f(t)}: The “L” is used to note that the function {f(t)} laplace transform is being applied.
F(s) : When working with Laplace Transform anything noted with a capital means you are working in s domain. Therefore, F(s) means the function f(t) is already transfer in the s domain.
{F(S)}: is used when working on the inverse laplace transform therefore going back to your function in the t domain.
Posted in Uncategorized
As we proceed through the course, we are usually given a first-order differential equation that could be solved. However, there are a lot of problems that cannot be solved. The first order equations could be divided into the linear equation, separable equation, nonlinear equation, exact equation, homogeneous equation, Bernoulli equation, and non-homogeneous equations. However, most of the separable and exact equation cannot always be presented the solution in an explicit form. It’s hard to find the value for a particular point in the function. There are some of the equations that do not fall into any of the categories above. So we introduce the method called Euler’s Method. We will be able to use it to approximate the solutions to a differential equation. In the Euler method, we will be given a differential equation which is the slope of a function, and define a step size for the integral ( the smaller steps sizes you have, the more accurate approximation values you will be get ). We generate a new point by starting at an initial point, we plug in this point into the given function, this will be the slope of the initial point. Then, then next new point will be the 
%3Dy_n%2Bhf(t_n%2Cy_n))
Now, we introduce an improved Euler’s Method. This method is quite similar to the Euler’s method. In the Euler’s Method we approximate the function by a rectangular shape (see graph below):
However, this approximate does not include the area that under the curve. To improve the approximation, we use the improved Euler’s method.The improved method, we use the average of the values at the initially given point and the new point. We define the integral with a trapezoid instead of a rectangle. The trapezoid has more area covered than the rectangle area. It will also provide a more accurate approximation.
It is hard to predict the solution curve is concave up or concave down in reality. The ideal prediction line would exactly hit the curve at next predict point. The Euler’s Method generates the slope based on the initial point, and we don’t know if the next point will be on this slope line, unless we use a computer to plot the equation. Sometimes, we might overestimate the value or underestimate the value. The Improved Euler’s Method addressed these problems by finding the average of the slope based on the initial point and the slope of the new point, which will give an average point to estimate the value. It also decreases the errors that Euler’s Method would have.
The improved Euler’s Method simply divided into three steps as following:
Steps in Improved Euler’s Method:
Step 1 find the
Step 2 find the
Step 3: find
Given a first order linear equation y’=t^2+2y, y(0)=1, estimate y(2), step size is 0.5.
Summary 
Note: it is very important to write the )
)
I think this video is pretty helpful, and make a clear point on the improved Euler’s Method and a example include in the video. please check out this video.
Overview
We are considering methods of solving second order linear equations when the coefficients are functions of the independent variable. We consider the second order linear homogeneous equation
P(x) d2 y/ dx2 + Q(x) dy/ dx + R(x)y = 0 (equation 1)
Since the procedure for the non-homogeneous equation is similar. Many problems in mathematical physics lead to equations of this form having polynomial coefficients; examples include the Bessel equation
X2 y’’ + xy’ + (x2 – a 22) y = 0
Where (a) is a constant, and the Legendre equation
(1 – x 2 ) y’’ – 2xy’ + c(c + 1) y = 0 Where (c) is a constant
Given the equation
P(x) d2 y/ dx2 + Q(x) dy /dx + R(x)y = 0
The equation
d2 y/ dx2 + Q(x) P(x) dy/ dx + R(x) P(x) y = 0 or d2 y/ dx2 + p(x) dy/ dx + q(x)y = 0
Where p(x) = Q(x)/ P(x) and q(x) = R(x) /P(x)
is called the equivalent normalized form of equation. The point (a) is called an ordinary point of equation (1). That is to say that these two quantities have Taylor series around x=x0. We are going to be only dealing with coefficients that are polynomials so this will be equivalent to saying that
for most of the problems. The basic idea to finding a series solution to a differential equation is to assume that we can write the solution as a power series in the form,
Y(x)= ∑_(n=0)^∞▒〖An (x-Xo)^n〗
and then try to determine what the an’s need to be. We will only be able to do this if the point x=x0, is an ordinary point. We will usually say that is a series solution around x=x0.
Example
y”+y=0
Suppose that has a Taylor series about x=0
y(x) = xn = a0+a1x+a2x2+a3x3+a4x4
Substitute into the differential equation and simplify by grouping together terms with similar powers of
We start with the assumption that
Y(x) = a0+a1x+a2x2+a3x3+a4x4 + …..
Y’(x) = a1+2a2x+3a3x2+4a4x3 +……
Y”(x) = 2a2+6a3x+12a4x2+……
Now substitute and into the differential equation
Y’’+y= 0:
(2a2+6a3x+12a4x2+……) +( a0+a1x+a2x2+a3x3+a4x4 + …..) = 0
Get rid of parentheses (don’t forget to distribute the and the in front of the second and third sets of parentheses
2a2+6a3x+12a4x2+…+ a0+a1x+a2x2+a3x3+a4x4 + ….= 0
Now group together by powers of :
(2a2+a0)+ (6a3+a1)x +(12a4+a2)x2+(20a5+a3)x3+…= 0
Finally, we compare each term on the left with the corresponding term on the right – since the right side is zero, each of the expressions in the parentheses (which give the coefficients of the powers of ) must also be equal to zero:
Then you find the first 5 terms ( coefficients)
This gives us the coefficients to determine the first five terms of the Taylor Series, Remembering that Y(x) = a0+a1x+a2x2+a3x3+a4x4 +…. we substitute in the values of to obtain
Y=a0+a1x+a0/2 x2 +a1/6 x3 + a0/24 x4
3. In case I wasn’t clear enough with the explanation or steps needed to solve the equation i will add a couple of video hopefully they help.
Posted in Uncategorized
Hi everyone,
The grades for Exam 3 are posted on the Grades page (email me if you have forgotten the password).
This exam covered a great deal of material and, while overall grades were comparable to the first exam, I’m sure not everyone did as well as they would have liked. You may improve your score on the exam by completing the Special Offer below.
Let me know if you have any questions, and best of luck with your studying!
Prof. Reitz
Exam 3 Special Offer – earn bonus points. You can improve your grade on the exam, by doing the following:
Laplace transform is a method used to go from one domain to another domain. In this case we go from the time domain (t) to the frequency domain (s).
As for most conversions, if there is one way to go from one unit to another, there should be a way to go backwards. It applies in this case also, although it isn’t necessarily a unit. In this case it’s simply called “Inverse Laplace Transform”. In this case we go from the Frequency domain (s), back to the time domain (t).
The notation for the Laplace transform is:
The “L” is used to denote Laplace transform. What is inside the curly braces is the function you want to transform from the time domain to the frequency domain.
You may sometimes also see this notation which means the same as the one before:
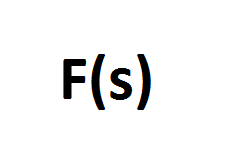
As for the Laplace transform, it is denoted:
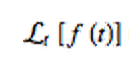
This will give you F(s).
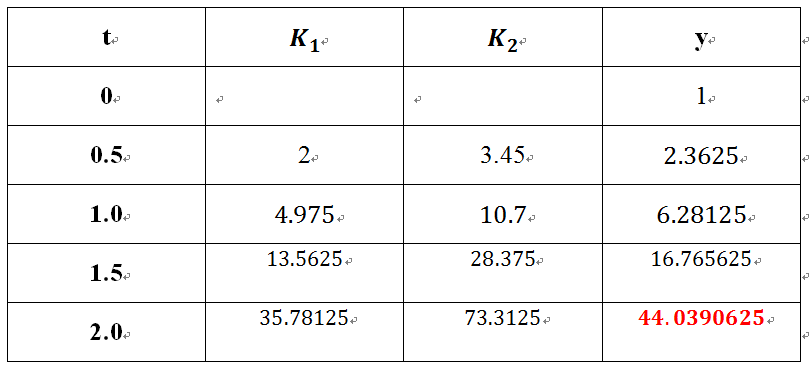
In order to get to the original time domain, you need to take the inverse Laplace transform of F(s) which is:
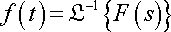
Now that we got the notation down for the Laplace transform we can go into more depth.
The general formula for the Laplace transform where ‘t’ is greater than or equal to zero:
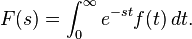We evaluate at t is greater than or equal to zero because we want to satisfy two conditions:
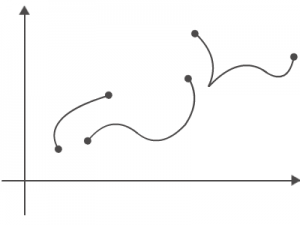
1. The function f(t) has to be piecewise continuous from the interval [0,A]. Simply means a function that is broken apart into different pieces but still continues on. For example:
2. The same function f(t) must be of exponential order. This means that the function f(t) must be smaller than or equal to ke^(at) when t is grater than or equal to M. In this case the variables K, M, and a are just constants and K, M are positive.
As for the inverse Laplace transform, there isn’t any set equation or method of doing it. The way the inverse Laplace transform is denoted, is by the following:
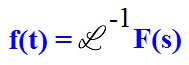
It simply mean to get the function f(t) you would need to take the inverse Laplace transform of F(s).
The main reason we use Laplace transform is because it makes certain (not all) differential equations easier.
A small introduction on the steps to take when solving a Laplace transform problem. There are five steps that we can use to solve a differential equation using Laplace transform:
1. Have a differential equation to solve
2. Take the Laplace transform of both sides in the equation. This will give you a simple algebraic equation to solve.
3. Solve the algebraic equation
4. Simplify the algebraic so you have what you are solving for on the left side and what it is equal to on the right side. If you can simplify the right side it will make it easier. Once simplified use partial fractions to solve for the unknowns.
5. Take the inverse Laplace transform and you will have your solution for the differential equation.
The OpenLab is an open-source, digital platform designed to support teaching and learning at City Tech (New York City College of Technology), and to promote student and faculty engagement in the intellectual and social life of the college community.
)
)
%3Df(t_n%2Bh%2Cy_n%2Bh((k_1%2Bk_2)%2F2)))
