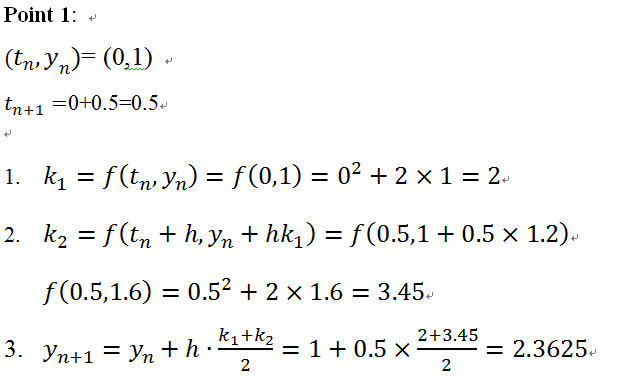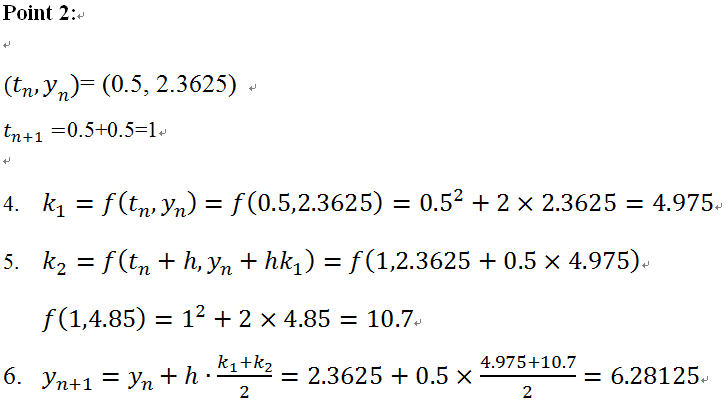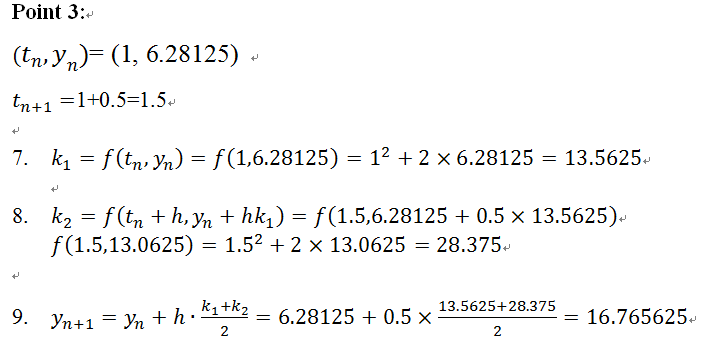Tag Archives: Improved Euler’s Method

As we proceed through the course, we are usually given a first-order differential equation that could be solved. However, there are a lot of problems that cannot be solved. The first order equations could be divided into the linear equation, separable equation, nonlinear equation, exact equation, homogeneous equation, Bernoulli equation, and non-homogeneous equations. However, most of the separable and exact equation cannot always be presented the solution in an explicit form. It’s hard to find the value for a particular point in the function. There are some of the equations that do not fall into any of the categories above. So we introduce the method called Euler’s Method. We will be able to use it to approximate the solutions to a differential equation. In the Euler method, we will be given a differential equation which is the slope of a function, and define a step size for the integral ( the smaller steps sizes you have, the more accurate approximation values you will be get ). We generate a new point by starting at an initial point, we plug in this point into the given function, this will be the slope of the initial point. Then, then next new point will be the  plus  step size h time the previously calculated slope. the general formula is, However, the error for the Euler’s Method depends on the step size. the only way to decrease the error is to reduce the step size, but it will increase the amount of calculations. it only roughly decreases the error by half.

Now, we introduce an improved Euler’s Method. This method is quite similar to the Euler’s method. In the Euler’s Method we approximate the function by a rectangular shape (see graph below):

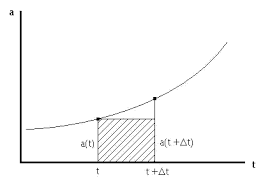However, this approximate does not include the area that under the curve. To improve the approximation, we use the improved Euler’s method.The improved method, we use the average of the values at the initially given point and the new point. We define the integral with a trapezoid instead of a rectangle. The trapezoid has more area covered than the rectangle area. It will also provide a more accurate approximation.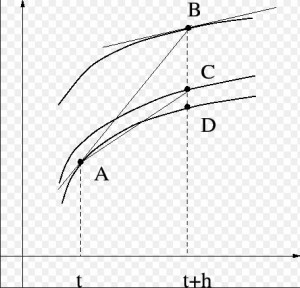

It is hard to predict the solution curve is concave up or concave down in reality. The ideal prediction line would exactly hit the curve at next predict point. The Euler’s Method generates the slope based on the initial point, and we don’t know if the next point will be on this slope line, unless we use a computer to plot the equation. Sometimes, we might overestimate the value or underestimate the value. The Improved Euler’s Method addressed these problems by finding the average of the slope based on the initial point and the slope of the new point, which will give an average point to estimate the value. It also decreases the errors that Euler’s Method would have.

 Given a first order linear equation y’=t^2+2y, y(0)=1, estimate  y(2), step size is 0.5. 

Summary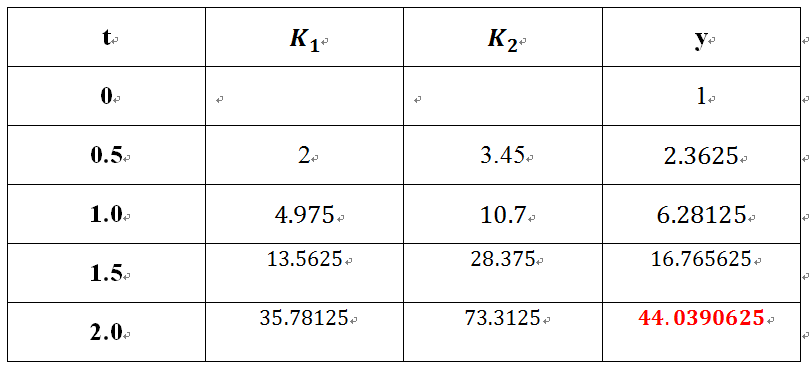 

Note: it is very important to write the and  at the beginning of each step because the calculations are all based on these values. This method involved with a lot of calculations, it is recommended after each point, write the values in a table. It will be easy for yourself to look up and check. For each point, the calculations approach to the next new point are the same, so if you set up the three steps, it will be very clear for you to continue to the next step.

I think this video is pretty helpful, and make a clear point on the improved Euler’s Method and a example include in the video. please check out this video.