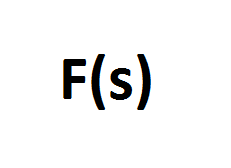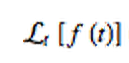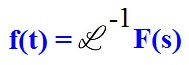The Laplace transform is an important technique in differential equations, and it is also widely used a lot in electrical engineering to solving linear differential equation The Laplace transform takes a function whose domain is in time and transforms it into a function of complex frequency.
The inverse Laplace transform does exactly the opposite, it takes a function whose domain is in complex frequency and gives a function defined in the time domain.
The steps to using the Laplace and inverse Laplace transform with an initial value are as follows:
1) We need to know the transformations we have to apply, which are:
L{y’}=sY(s)-y(0) L{y”}=s^2 Y(s)-sy(0)-y'(0)
2) Once we apply the proper Laplace transform to our function we then apply the initial condition
3)Then since we can’t find y(t) directly, we solve for Y(s), which is the Laplace transform of y(t)
4) Once we find Y(s), we may need to break up the equation into partial fraction form depending on the denominator. there must only be a single term in the denominator and no “s” in the numerator. (look at “Factor in Denominator” chart image attached)
5) We take the inverse Laplace transform to get y(t)
So now to apply those steps,
Let’s take for example, 2y’-y = 1 ; y(0) = 0
1) Apply the transforms. 2(sY(s)-y(0))-Y(s)= 1/s
2) Apply the initial conditions given. 2(sY(s)-0)-Y(s)= 1/s
3) Solve for Y(s). Y(s)(2s-1) = 1/s Y(s)=1/s(2s-1)
4) Apply the inverse transform. L^(-1){1/s(2s-1)} = L^(-1){1/(2s-1)-(1/s)} = e^(1/2t)-1
For another example, let’s take something that requires us to use partial fractions to get the right denominator.
F(s) = [19/(s+2)]-[1/(3s-5)]+[7/(s^5)]
So to get started on this one, we look at the Laplace transform table and see which fraction refers to the transformation. The first fraction looks like 1/(s-a) = e^(at). Although the “a” in this case would be a -2. For the second fraction, we got the same case except that the s is 3s, so all we have to do is factor out the 3, and apply the Laplace transform. And for the third fraction we see that it looks like, (n!)/s^(n+1) = t^n ; and since the exponent in the denominator is 5, the value for n = 4. But now we still have a 7 in the numerator whereas we need a 4! or 24. So to fix this all we have to do is multiply the top numerator by a constant to achieve the desired numerator, but we have to remember to divide by the same constant after taking the Laplace transform.
So it would be:
F(s) = [19/(s-(-2))]-[1/3(s-(5/3))]+[7(4!/4!)/(s^(4+1))]
So, now we have to take the inverse Laplace transform.
f(s) = 19e^(-2t) – (1/3)e^(5t/3) + 7/24(t^4)
I hope that the link to the video and images are helpful.
We evaluate at t is greater than or equal to zero because we want to satisfy two conditions:
