Euler’s Method

When given a first order differential equation, we may use the various types of strategies that we earned such as exact, linear, separable, etc. Sometimes these strategies do not help us solve the equation meaning we can’t find an explicit solution (can’t find y=…). This is where Euler’s method comes into play. Euler’s method helps us find an approximation for the solution of a differential equation by generating a series of points. . The foundation for Euler’s Method is to use the concept of local linearity to join the multiple small line segments so that they make a close approximation to the function.

• Definition of local linearity: if you zoom in (using the same zoom factor in both directions) on a point on the graph, the graph eventually appears to be a straight line whose slope is the same as the slope (derivative) of the tangent line at that point.

Euler’s Method Formula: y_n+1=y_n + h*f(t_n,y_n)

 For Euler’s Method we are given useful information (“givens”) to help us find y_n. The givens are:

• The differential equation y’= f(t_n,y_n)

NOTE: This helps us find the slope for the points by plugging in the points into the equation.

• Initial value point y(t₀)=y₀, also written as (t_0,y_o)

NOTE: We use our initial value to find

(t_1,y₁)

(t_2,y₂)

(t_3,y₃)

.

.

     (t_n,y_n)

 

• The step size h. (optional)

NOTE: When the step size is not given, it is up to your discretion to decide whether you want a close approximation or not. Recall, in Calculus I, we learned how to find the area under the curve. The basic idea is to use smaller rectangles under that curve, so our area approximation can be close as possible to the actual area. This idea is the same for the step size, the smaller your step size is from one point to the other, the closer your approximation for the point y(t_n)= y_n will be. Also, because of the step size we are allowed to find the values of the succeeding t’s by adding the step size to the preceding t.

Sample Problem:

Given y’= t²+3t-1, y(0)=1. Find the value of  y(2).

Step 1:

We have to decide on the step size (h) to find the next series of points until we get to y(2) . A good guess for an approximation may be 0.5. It depends on how many steps you would like to use. Let’s say I want to use 5 steps. A formula to let me know what my value of h will be:

 

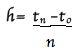 where n= the steps that will be used. Let’s plug it in and see if the guess will give me a better approximation

So, we were off by 0.1. We will use 0.4.

Step 2: Find the “t”s

We use our step size and add on to the previous t

t₁= t_o + 0.4 = 0 + 0.4 = 0.4

t₂= t₁ + 0.4 = 0.4 + 0.4 = 0.8

t₃= t₂ + 0.4 = 0.8 + 0.4 = 1.2

t₄= t₃ + 0.4 = 1.2 + 0.4 = 1.6

t₅= t₄ + 0.4 = 1.6 + 0.4 = 2

NOTE: Last Step size should be the value that are ask to find, y(2)

 

Step 3: Finding our slopes to find our “y”s. We use the Euler’s Method formula to find our slope first, in order to find the succeeding y. It’s like recursive sequences, we cannot proceed to the next points without the preceding data from the previous equation.

y_n+1=y_n + h*f(t_n,y_n)

What we know:

• Previous “y”s
• How to find the slope
• h=0.4

y₁=y₀ + 0.4 x ((0) ²+3(0)-1)= 1+0.4(-1)=0.6

y₂=y₁ + 0.4 x ((0.4) ²+3(0.4)-1)= 0.6+0.4(0.36)=0.744

y₃=y₂ + 0.4 x ((0.8) ²+3(0.8)-1)= 0.744+0.4(2.04)=1.56

y₄=y₃ + 0.4 x ((1.2) ²+3(1.2)-1)= 1.56+0.4(4.04)=3.176

y₅=y₄ + 0.4 x ((1.6) ²+3(1.6)-1)= 3.176+0.4(6.36)=5.72

 

A table is also helpful when finding the solution.

 

Subscript	t	y	y’
0	0	1	(0) 2+3(0)-1=-1
1	0.4	0.6	(0.4) 2+3(0.4)-1
2	0.8	0.744	(0.8) 2+3(0.8)-1
3	1.2	1.56	(1.2) 2+3(1.2)-1
4	1.6	3.176	(1.6) 2+3(1.6)-1
5	2	5.72	(2) 2+3(2)-1

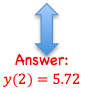
Note: You can also see a visual of Euler’s Method (graphically) using graphic software. The graph below is from www.mathscoop.com

 

Here is another great example: