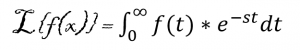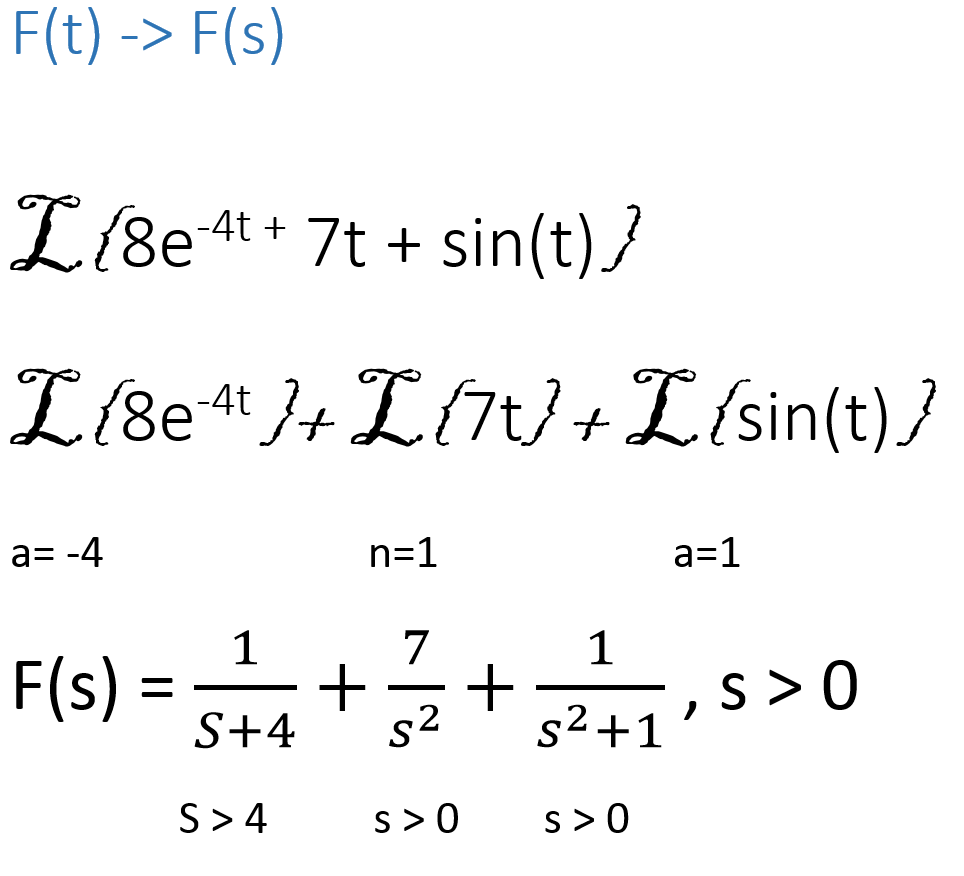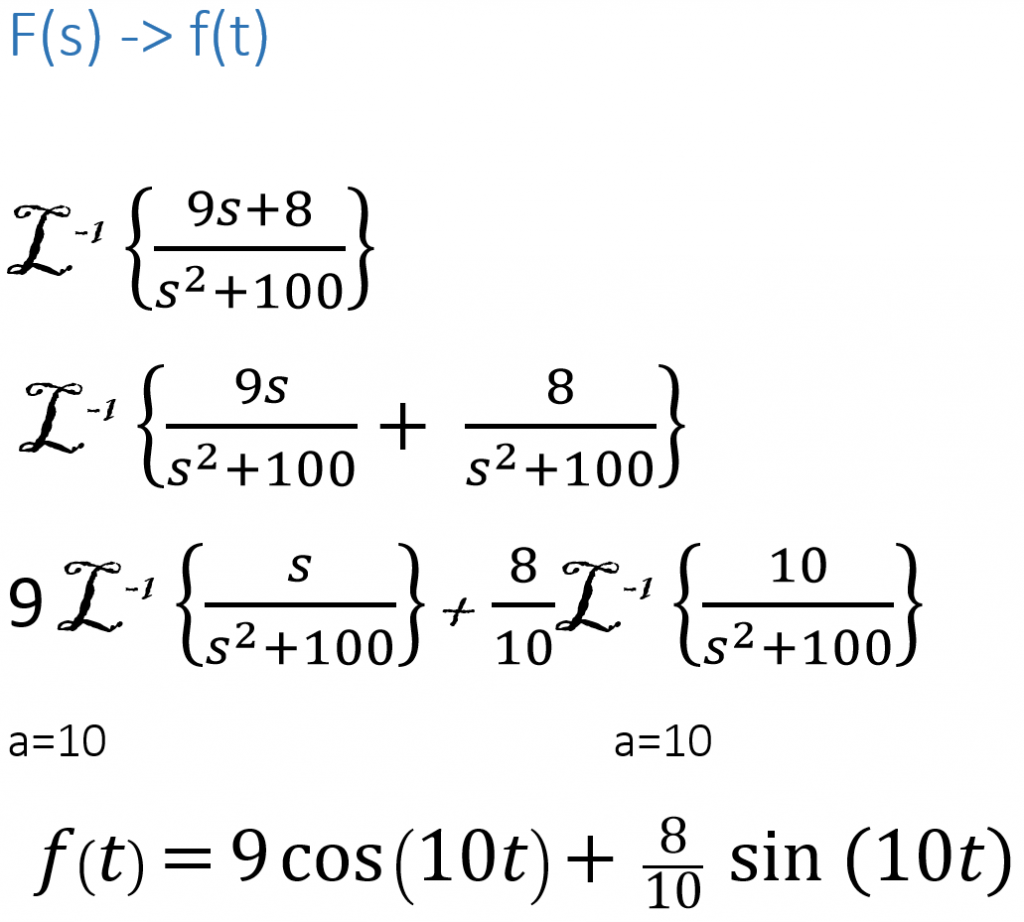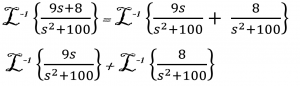Laplace transformation “transform” a differential equation into an algebraic equation by changing the equation from the time domain to the frequency domain. The differential equation is packed into one or more Laplace transform equivalent forms and manipulated algebraically.

If we apply the Laplace transformation correctly we can save a lot of time and effort. Even when the complexity of the operation required are reduced significantly, it is necessary to pay attention to the parameter contained in the Laplace transformation table.

The following equation to convert an equation from the time domain to the frequency domain:

To avoid having to do this process every single time a transform table has been created. This table can be used to convert f(t) into its F(s) equivalent and can be used to bring F(s) back into f(t). The transform table has some important parameter such as the values for “s” that are valid for that specific equation. This is the domain of convergence for that equation and is very important to understand it in order to apply the Laplace transform correctly.

Importance of the “s” value: “s>0” and “s>a”

 

In the following example we can see the reason for the restriction: “s > 0”. When we evaluate the integral for “s > 0” the integral converges to 1/s, but when we plug-in zero, the integral diverges and we have no solution for the integral.

Let’s take the Laplace of 1:

Fitting the equation into the Laplace transform table:

 

Sometimes the given equations doesn’t seem to fit any of the forms in the transform table. To solve this problem we have to use algebraic techniques to brake the equation into parts that fit the transform table. For example:

 

 

Laplace transform in 5 steps:

1.    Start with a differential equation.

The first steps is have a differential equation f (t).

2.    Take Laplace transformation of both sides.

The transformation has to be taken entirely on both sides of the differential
equation. Sometimes the differential equation doesn’t match the transform table
and we have to use algebraic techniques to force it to match. For example:

separate the parts of the equation connected by addition or subtraction,
to match the table, find the values for a and/or be as required by the table:

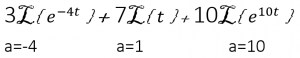
Make sure you input the “a” value correctly (check for the sign)
state the values for convergence. In this case “s > 0” since all
individual pieces of the equation converge when “s> 0”

3.    Solve the resulting equation.

Once we have the equation in the frequency domain we can solve for
Laplace of y: L {y}

4.    Simplify the solution.

Once we found   L {y} we will proceed to reverse process done
in part 2, to match the transform table we might need to use
partial fractions or other algebraic techniques to separate the
Solution into parts that match the table.
As in step 2 watch carefully for the values of “a “and/or “s”

Example:

5.    Take the inverse Laplace.

Once the solution is simplified we take inverse Laplace to bring
the equation back to time domain.

a pdf copy of this document available here: Laplace transformation