Non-homogeneous differential equations are the same as homogeneous differential equations, However they can have terms involving only x, (and constants) on the right side. The interesting part of solving non homogeneous equations is having to guess your way through some parts of the solution process.
You also can write non-homogeneous differential equations in this format: y” + p(x)y’ + q(x)y = g(x).
The Reason I’ve chosen this problem is because it basically touches every aspect of a Non-homogeneous second order differential Equation using methods of undetermined coefficients.
y” + 6y’ + 9y = -578 sin 5t
The first step when dealing with undetermined or constant coefficients is getting the Characteristic equation. Which will later become the first half of our solution.
y” + 6y’ + 9y = 0
r^2 + 6r + 9 = 0
( r+3 ) ( r+3) = 0
R1 = -3 R2 = -3
When solving the characteristic equation sometimes we run into repeated roots. In this case we must use the following formula y = C1e^r1(t)+C2 (t)e^r2(t)
y (t) = C1e^-3t + C2te^-3t
After finding the characteristic equation our next step in this linear equation is to guess the y. In this case our y is going to include both sin and cosine. We make this guess because the cosine is going to come up eventually when finding the derivative and by adding it into the equation, it will allow us to cancel it out later on throughout the steps in the solution process. We also will need to find the y’ and y”.
y = C sin (5t) + D cos (5t)
y’ = 5 C cos (5t) – 5 D sin (5t)
y” = -25 C sin (5t) + 9 D cos (5t)
Now we plug it back into its original equation.
-25 C sin (5t) – 25 D cos (5t)
+30 C cos (5t) – 30 D sin (5t)
+9 C sin (5t) + 9 D sin (5t)
= -578 sin 5(t)
At this point we want to cancel and group any like terms.
(-16C -30D) sin (5t) + (-16D + 30C) cos (5t) = -578 sin (5t)
Resulting two equations.
(-16) (C) – (30) (D) = -578
(30) (C) – (16) (D) = 0
Now we must find Find C & D
(30) (C) – (16) (D) = 0
+16 (D) +16 (D)
C = (16/30) (D)
Now we plug in C back into the next equation.
(-16)(16/30D) – (30) (D) = -578
(-256/30)(D) – (30) (D) = -578
(-578/15)D = -578
D = 15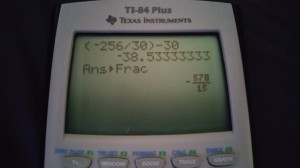
When calculating the (-256/30)(D) – (30) (D).
We use the calculator to find the fraction value by entering math > frac > enter.
Plug in D
C = (16/30) (D)
C = (16/30) (15)
C = 8
After finding all values we’re finally ready to plug in all variables and combine the homogeneous equation with its general solution.
Resulting in:
y (t) = C1e^-3(t) + C2(t)e^-3(t) + 8 sin 5(t) + 15 cos 5(t)
If we were given the case of finding a particular solution, we will have to take this a few steps further to and plug in the (t) value. But fortunately for us this general solution will suffice.
Below I have included videos that has helped me understand how to solve Non-homogeneous second order differential Equations using methods of undetermined coefficients. Khan academy has been an incredible help in the understanding of all things in relation to differential equations.
Problem listed above was taken from the midterm review, question 9 by Professor JReitz.



