Due date: Tuesday, October 24, 2:30pm
Individual topics will be assigned later. More details will be added later.
In addition to a presentation in class, your assignment is to include the following items in your ePortfolio:
- The statement of the theorem/result that you have been assigned, written in
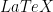 , in the body of the post. You may copy this statement word-for-word from the text, or paraphrase it. Either way, it must be complete and precise.
, in the body of the post. You may copy this statement word-for-word from the text, or paraphrase it. Either way, it must be complete and precise.
- A link to a GeoGebra dynamic worksheet (uploaded to GeoGebra Tube) that helps students understand the statement of your theorem. The dynamic worksheet should be completely self contained. Think of the worksheet as playing the following role: You are teaching a geometry course and will be absent for one class. The lesson for that day is the topic you have been assigned for this project. The substitute teacher assigned to cover your class does not have a background in geometry, so your students will have to learn the topic exclusively from your dynamic worksheet. Your worksheet must take advantage of the benefits GeoGebra has over traditional paper worksheets (for example, you should make use of the drag test).
You may also include extra details either in the body of your post or in the dynamic worksheet, if you think they will be helpful. For example, you may include hints for the proof of your statement (why is the statement true?) or you may include helpful applications. These are optional and should only be included if they help students understand the statement.
There are many resources available online for help creating dynamic worksheets. Here’s one. Read Chapter 3 of the Venema text for other helpful tips. As a sample, here is the dynamic worksheet on Ceva’s theorem that we will explore in class.
Once again, your classmates will be asked to score your worksheet and offer detailed feedback. This will be similar to the rubric and feedback form for the Desmos mini-project.
Topic assignments



Recent Comments