By Sierra Morales and Oscar Pais
In this video we will solve an undamped spring system problem which requires the application of a linear second order equation to solve. This particular problem focuses on the variables associated with the system’s equilibrium, spring elongation and an initial velocity.
Key concepts to understanding this problem are:
- Newton’s Second Law of Motion: Force = mass * acceleration
- Hooke’s Law: spring Force = – spring constant * spring stretch or compression
We will be using the following second order differential equation to solve this problem:
\begin{math} y” + \frac{k}{m} \:y\:=\:0 \end{math}
Where:
- y” represents the an acceleration or deceleration
- k is the spring constant
- m is mass
- y is a displacement value
Note: This problem does not list a value for mass. If you notice the fraction \begin{math} \frac{k}{m} \end{math} has m in the denominator, knowing that that value could not be zero you could either treat \begin{math}\frac{k}{m} \end{math} as a computed value as we did or assign a value of one to mass.
Ultimately our solution will take the form of:
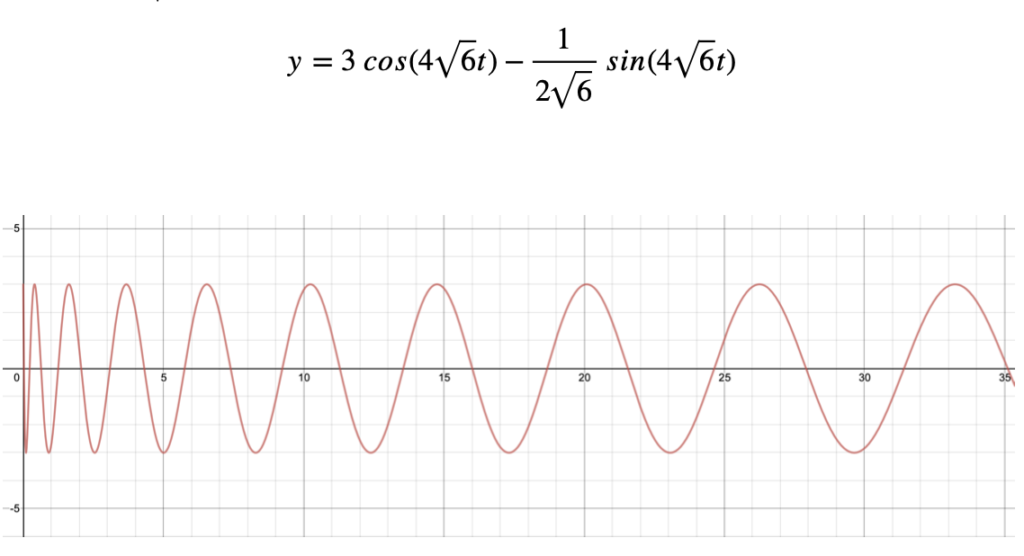
Applying a bit of intuition to this graph shows that over time the frequency of the oscillations begin to decrease, that is to say a lower frequency. However, since this is an undamped spring system notice that the amplitude never decreases. That is the spring system has the ability to restore all of its energy in compression and elongation.
Video Lesson:
https://www.dropbox.com/s/4q5klxo489chygu/RPReplay_Final1606190322.MP4?dl=0
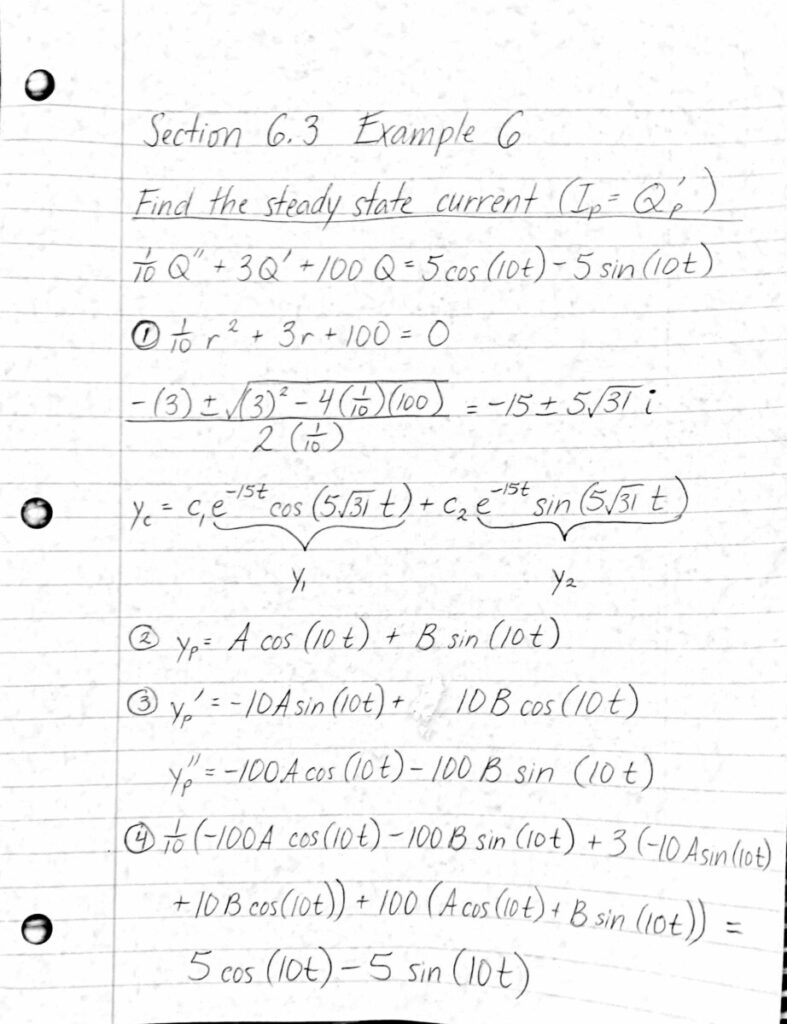
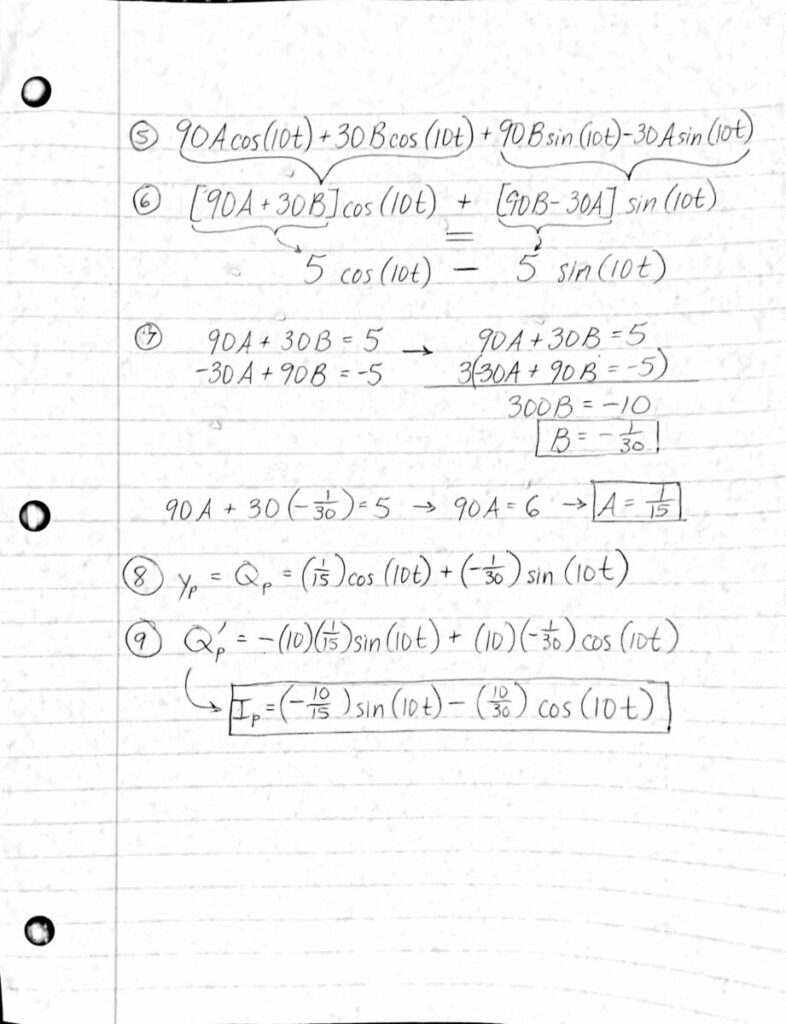



Recent Comments