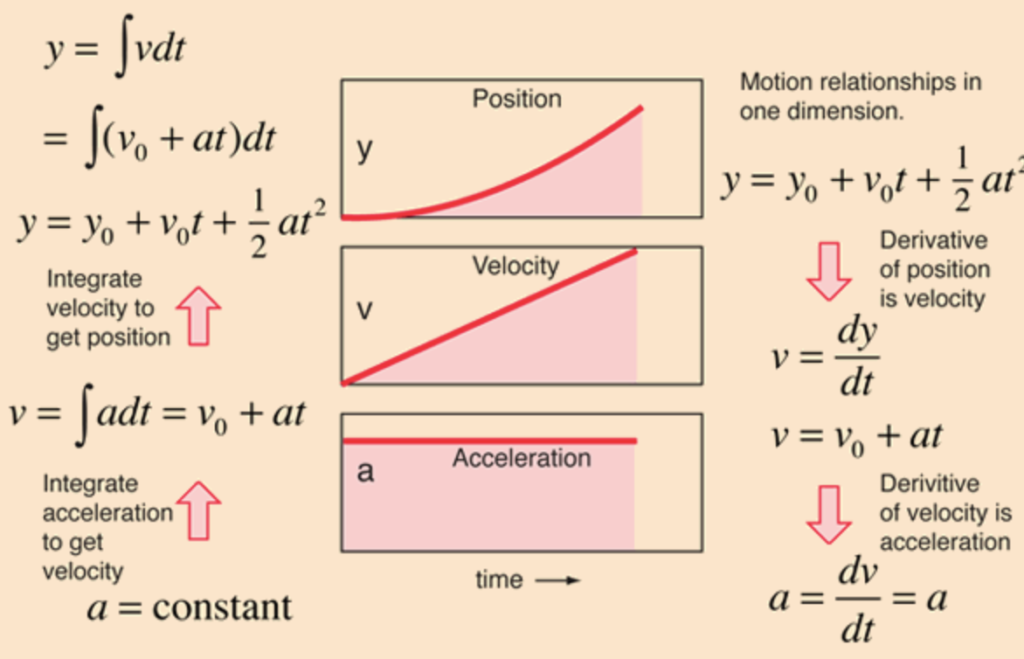
General form of a Differential Equation Involving Growth and Decay
$Q’=\frac{dQ}{dt}$
Growth and decay problems are commonly generalized under the exponential model,
$Q’=aQ$
$a$ would be the constant of proportionality.
Upon quick inspection, we can treat this model as a separable equation. Thus, the solution for this differential equation will be:
$Q=ce^{at}$
For IVPs, the solution would be,
$Q=Q_0e^{a(t-t_0)}$
where $Q_0$ is the value/function of $Q$ at a given time, and $t_0$ is a given value of time. We use $(t-t_0)$ because we solve for the value of $Q(t)$ at a given time period.
Quick Review
With,
$Q’=aQ$
We separate the variable $Q$ into one side of the equation,
$\frac{Q’}{Q}=a$
Then we integrate the entire equation with respect to $t$
$\int\frac{Q’}{Q} dt=\int (a) dt$
Integrating gives us:
$\ln(Q)=at+c$
Now we must solve for $Q$. To solve for $Q$, we use our natural logarithm and exponent rules,
$e^{\ln(Q)}=e^{at+c}$
Thus,
$Q=ce^{at}$
Applications
1.Radioactive Decay
What is radioactive decay? Radioactive decay is a natural phenomenon of certain materials “losing” ( i.e. decaying) energy and matter over time due to their unstable atomic nucleus. Recall that atoms are made of particles called protons, neutrons, and electrons; under radioactive decay, these three particles are ejected out of the atomic nucleus, thus, a radioactive material will lose mass over time.
The general exponential decay function is defined as:
$Q(t) = Q_0e^{-k(t-t_0)}$
$Q_0$ is the initial quantity, $-k$ is the is treated as the “decay constant”, $t_0$ is the initial time (essentially zero in most cases), and $t$ would be any time duration.
Since $\tau$, or the “half-life,” is the amount of time at which a radioactive material’s quantity is reduced to half, we can turn $Q(t)$ into,
$Q(\tau) = \frac{Q_0}{2} = Q_0e^{-k(\tau-t_0)}$
$\frac{Q_0}{2} = Q_0e^{-k\tau}$
where $t_0 = 0$ and $t = \tau$.
We then solve for $k$ by canceling like terms and taking the natural logarithm of the equation:
$\ln(\frac{1}{2}) = \ln(e^{-k\tau})$
((Recall that $\ln(\frac{a}{b}) = \ln(a)-\ln(b)$ and $\ln(1) = 0$))
$-\ln(2) = -k\tau$
$k = \frac{ln(2)}{\tau}$
If a given problem indicates that $Q_0$ lost a certain percentage, $P$, of its mass at a certain time, then we can set $Q(t) = PQ_0$.
For an IVP where $Q’=-kQ$ and $Q(t_0)=Q_0$, the general solution is the same as the exponential decay function:
$Q(t) = Q_0e^{-k(t-t_0)}$
2.Carbon Dating
Carbon dating is a process based on the concept of radioactive decay. The unstable isotope, Carbon-14, decays into the stable isotope, Carbon-12. By determining the ratio of Carbon-14 and Carbon-12 in deceased organisms, scientists can determine the age of an organism– higher levels of Carbon-14 in a sample means that an organism died at a more recent time period.
Carbon dating uses the same function for radioactive decay problems, $Q(t) = Q_0e^{-k(t-t_0)}$. Most problems, however, have us solve for $t$. Also, unless otherwise stated, $t_0=0$.
Step-by-step solution for ‘t’
(See “Radioactive Decay” section for finding $k$)
From $Q(t) = Q_0e^{-k(t-t_0)}$, we have,
$\frac{Q(t)}{Q_0}=e^{-k(t)}$
Take the natural logarithm of the equation to have,
$\ln(\frac{Q(t)}{Q_0})=\ln(e^{-k(t)})$
$\ln(\frac{Q(t)}{Q_0})=-k(t)$
Finally, solve for $t$,
$t=\frac{-\ln(\frac{Q}{Q_0})}{k}$
3.Continuously Compounding Interest
The concept of compounding interest applies to savings accounts, loans, credit cards, or most financial services that involves “interest.” Essentially, a certain amount grows in value at a specified percentage at specified intervals of time.
The general formula would be:
$Q(t) = Q_0(1+\frac{r}{n})^{nt}$
$Q_0$ is the initial amount deposited or owed, $r$ is the annual rate or interest rate, $n$ is the number of times per year interest is compounded, and “t” would be the number of years.
Semi-annually would mean $n=2$, quarterly is $n=4$, monthly is $n=12$, and daily is $n=365$. Also note that $r$ should be written in it’s decimal form.
Recall that,
$\lim_{n \to \infty} (1+\frac{r}{n})^{n}=e^{r}$
Therefore, if we infinitely compound interest, then we have this function,
$Q(t)=\lim_{n \to \infty} Q_0(1+\frac{r}{n})^{nt}=Q_0 e^{rt}$
The solution then to an IVP regarding continuously compounding interest where $Q’=rQ$, $Q(t)=Q_0$, and $t=0$ is
$Q(t)=Q_0e^{rt}$
4.Mixed Growth and Decay
Mixed growth and decay is a general term for problems that involve rate of changes that increase and decrease a value simultaneously.
The general forms would be:
Form A
$Q’ =$ rate of increase of $Q$ – rate of decrease of $Q$
Form B
$Q’ =$ rate of increase of $Q$ + rate of increase of $Q$
Form C
$Q’ =$ rate of decrease of $Q$ – rate of decrease of $Q$
If one of the rate of changes are constant then, we’ll have
$Q’ = \pm a \pm cQ$
where $a$ would be a constant rate of change (negative or positive), and $cQ$ would be $Q(t)$ multiplied to a proportionality constant, which could also be negative or positive depending on the problem (recall the exponential model at the beginning of this post).
Notice that we now have a first order linear differential equation. To solve this type of problem, we can either use variation of parameters, separation of variables, integrating factors, transformations from Bernoulli equations and homogeneous equations, or substitution.
Example Situations
An example of general form A would be the production of a radioactive material (while it’s being produced (constant rate increase), the material radioactively decays (decrease)). Therefore, we have,
$Q’ = a – kQ$
$k$ is the decay constant, $a$ is the production rate, and $Q$ is the decay rate.
An example of general form B would be a savings program. Say a constant amount is periodically deposited (constant rate increase) and the entire balance of the savings account accrues interest(increase). Therefore, we have,
$Q’ = a + rQ$
$r$ is the annual interest, $a$ is the periodic deposit of a constant amount, and $Q$ would be rate of increase due to interest.
An example of general form C be a tank of water is leaking (decrease) while a person scoops out a constant amount at a steady rate (constant rate decrease). Therefore we have,
$Q’ = -a – cQ$
$-c$ would be proportionality constant, $-a$ would be the rate of water scooped out the tank, and $Q$ would be the rate of leakage.
Sample Problems
Example 1 (Denny/Sheyla)
A radioactive material will lose 34% of its mass in 55 minutes. What will it’s half life be?
Example 2 (Jennifer/Ariel)
A process creates a radioactive substance at a rate of 3 g/hr and the substance decays at a rate proportional to its mass, with a constant of proportionality, k = .05(hr)^-1. If $Q(t)$ is the mass of the substance at time, $t$, find limit of $Q(t)$ as $t$ approaches infinity.
Example 3 (Richard/Raisa)
Wonka’s factory makes 1000 pounds of chocolate per week, while the workers eat the candy at a rate equal to Q(t)/25 pounds per week, where $Q(t)$ is the amount of chocolate present at time $t$.
a. Find $Q(t)$ for t > 0 if Wonka’s factory has 350 pounds of chocolate at t = 0b. lim t —> infinity of $Q(t)$
Example 4 (Tushar /Shisir)
Students tend to use google chrome at an alarming increased exponential rate, with the usage on the browser doubling every 100 days. What is the exponential growth rate?
Example 5 (Brian/ Jian Hui)
A young Warren Buffet initially deposits 50 dollars into his savings account. He also tries to make monthly recurring deposits of 10 dollars every month. If his savings account has an interest rate of 0.05% APY, make a mathematical model to predict the value of his account at any point in time, where $t>0$




Recent Comments