Forgive the smooth brain energy in this post. I’m doing this with less than a day left before the deadline. Anyway…
Context
The Tacoma Narrows Bridge is a suspension bridge in Washington state, and was first constructed in 1937. It became infamous for collapsing in 1940 due to issues with vibrations (which can be modeled or analyzed with differential equations). This collapse prompted further studies into structural design and its relationship with vibrations.

Bridges are designed to be somewhat flexible to accommodate the expansion and contraction of materials due to temperature changes and to survive vibrations caused by wind, moving loads (moving pedestrians/cars), and earthquakes . Like tuning forks, structures have natural frequencies (naturally vibrating at a specific rates when disturbed). At the day of the Tacoma Narrows Bridge collapse, the bridge was reacting to strong winds that eventually matched the natural frequency of the bridge, causing greater oscillations and stress on to the bridge. The bridge was described to be twisting at each end in opposite directions.
There’s more physics involved in this, but I’m not really capable of explaining in detail. Winds make bridges wobble. Too much wobble equals broken bridge. Stiff bridge with too much wobble equals broken bridge too. Too flexible bridge makes for bad driving experience.
Relevance to Differential Equations
When studying second order linear differential equations, we define $f(x)$ in $y”+p(x)y’+q(x)y=f(x)$ as the “forcing function.”
In practical applications, the “forcing function” is the force affecting a system. When the forcing function matches a natural frequency, “resonance” is achieved and we find that the amplitude of the oscillations increase. So for a suspension bridge, under certain conditions, the wind will “excite” the structure due to resonance, inducing strenuous movement that will lead to structural failure.
To counteract (excessive) oscillations due to external disturbances, structures have systems that “damp” vibrations. Suspension bridges can be seen as a series of spring-mass systems, therefore, the concept of “damping” in spring-mass systems can be applied to suspension bridges. Remember that the roots of the characteristic equation of the differential equation describing a spring-mass system determine the level of “damping” in a system (underdamped, overdamped, critically damped).
The following equation is a model developed by a pair of mathematicians (Lazer and Kenna) to describe the simple behavior of a suspension bridge with no wind disturbances:
$\frac{d^2y}{dt^2}+\alpha\frac{dy}{dt}+\beta y+c(y)=-g$
Notice that this equation is a second order differential equation (which we might be able to consider as a linear equation, if the forcing function is $f(x)=-g-c(y)$
$\frac{d^2y}{dt^2}$ is the vertical acceleration of the bridge’s roadbed. $\alpha\frac{dy}{dt}$ is derived from damping.$\beta y$ “accounts for the force provided by the material of the bridge” pulling the roadbed to it’s neutral position. $c(y)$ “accounts for the pull of the cable” when the roadbed is displaced in either upward or downward direction.$ -g$ is the downward force due to gravity. $\alpha$ and $\beta$ are constants.
For conditions where wind disturbance is a factor, the model becomes:
$\frac{d^2y}{dt^2}+\alpha\frac{dy}{dt}+\beta y+c(y)=-g+\lambda \sin(\mu t)$
$\lambda \sin(\mu t)$ models a simplified oscillation caused by the wind.
Videos
References
No MLA or APA format but here are some links
Why the Tacoma Narrows Bridge Collapsed: An Engineering Analysis
Sound Waves and Music – Lesson 4 – Resonance and Standing Waves: Natural Frequency
5.4 Forced vibration of damped, single degree of freedom, linear spring mass systems.
Differential Equations:4th Edition by Paul Blanchard/Robert L. Devaney/Glen R. Hall
Help me. My brain is fried.

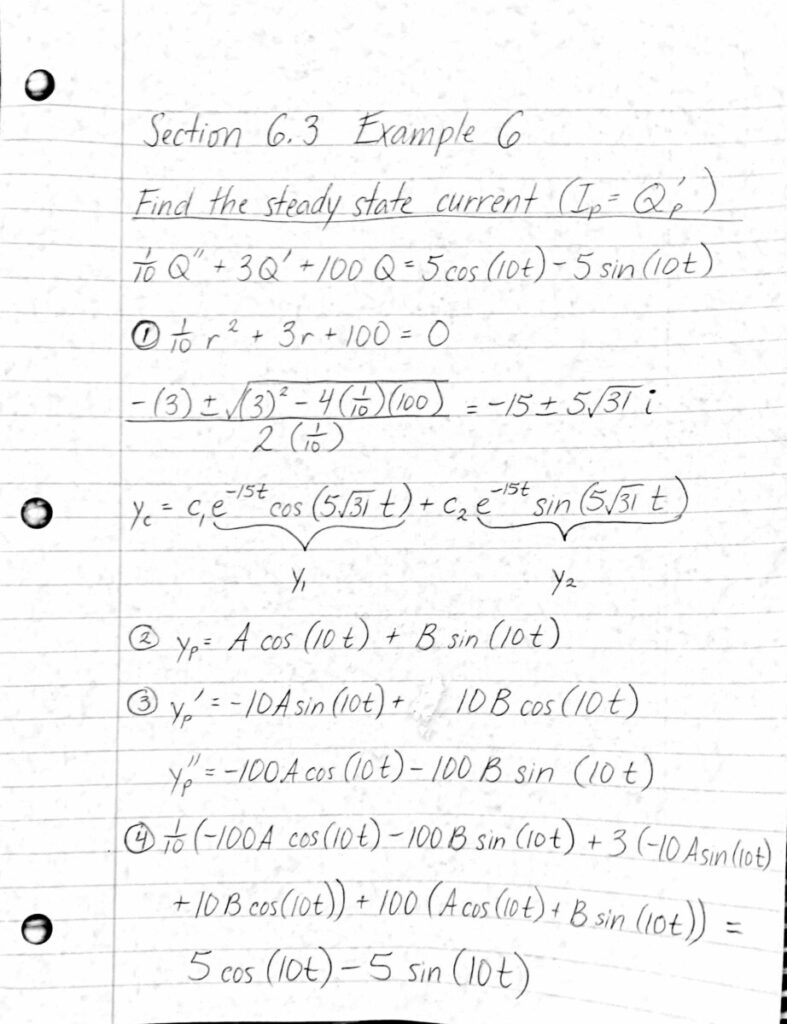
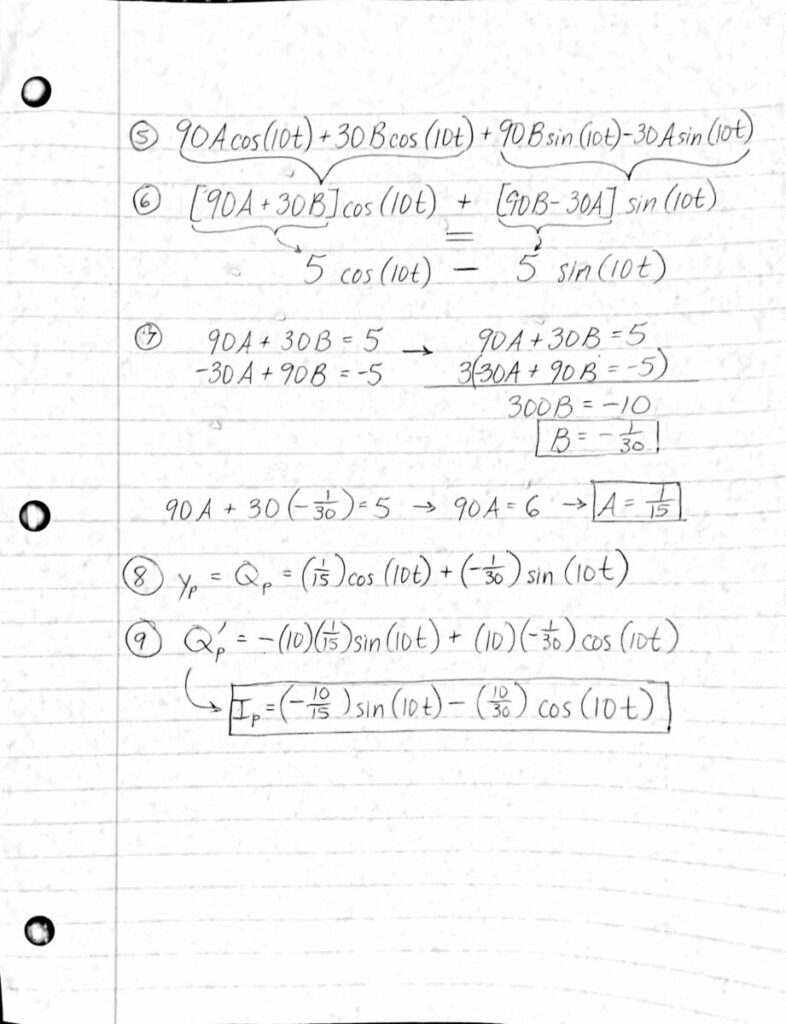



Recent Comments