Objective:
Learn how to apply differential equations to solve problems dealing with position, velocity and acceleration.
Introduction:
Mechanics is the general study of the relationships between motion, forces, and energy. In the past we have solved problems dealing with motion in one and two dimensions and even incorporated inclined planes and friction.
The incline and friction properties in previous courses were generally uniform in nature and did not change with respect to any other parameters. We solved these problems by analyzing the derivative of motion equations, that is to say the derivative of a function is the rate of change of the output value with respect to its input value. For example the velocity of an object is the change of its position with respect to time.
In this lesson we will be analyzing the relationship (differential equation) between motion parameters (functions) and their rates of change (derivatives). We will be using first order ordinary differential equations (ODE).
The parameters that we are going to be using will be standard units for length, mass, force, and time and are generally quantified in three standard systems: Centimeter-Gram-Seconds (CGS); Meter-Kilogram- Seconds (MKS); and Foot-Pound-Slug (British).
Parameters and Relationships:
Time (t)
Displacement/ Position (y): y = y(t)
Velocity (v): v = v(t) v = y’
Terminal Velocity (vt)
Acceleration (a)(): a = a(t) a = v’ a = y’’
Force (F): F = m a
Force of Gravity/ Weight (Fg): Fg = m g
Resistive Force (F1): F1= k|v| = -kv
Acceleration due to Gravity (g): 9.8 m/s2 (mks); 980 cm/s2 (cgs); 32 f/s2(British)
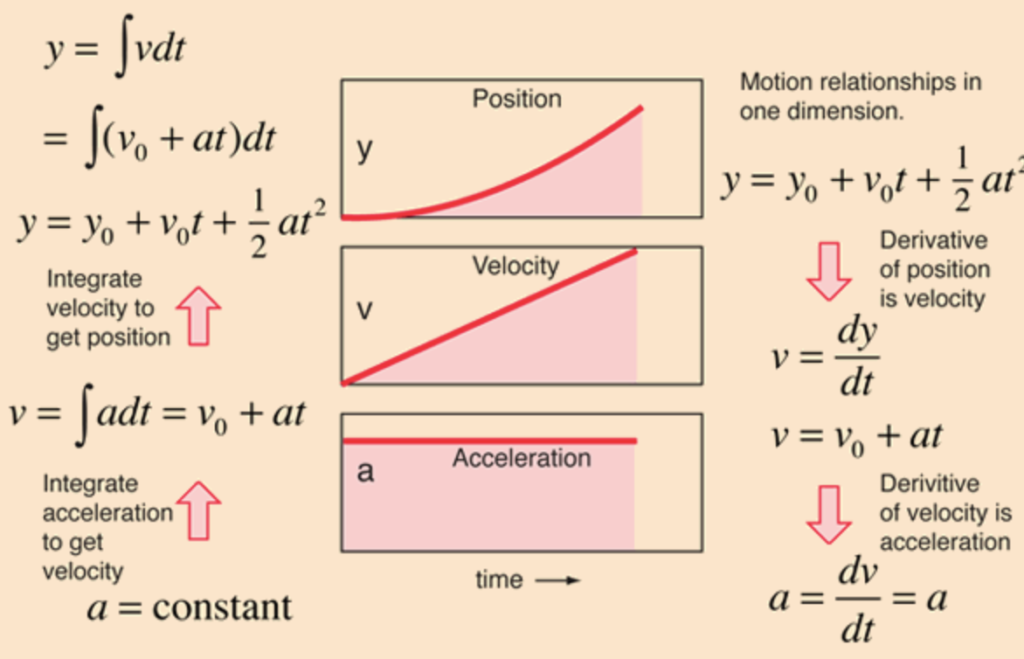
We will refer to an object’s displacement as the length measured from its original position to its final position, while we will say that distance is the total length traveled to its final position.
Velocity is the rate of change of position with respect to time. An example of this is a car’s speedometer which measures forward speed (velocity) in either miles per hour, or kilometers per hour. Velocity is the first derivative of position, the rate of change in position with respect to time.
Acceleration is the rate of change of velocity with respect to time. It is the first derivative of velocity, or the second derivative of position. We will constrain ourselves to only using First Order equations in this lesson.
Newton’s second law of motion asserts that for a constant mass (m), the force (F) and the acceleration (a) are related by the equation:
$F=ma$
This equation can be further defined by the form:
$F(t, y, y’) = my’$
Here we see that the force F may depend upon t, y, and y’. Remembering our constraint to use first order differential equations we will omit the use of y to attain the form:
$F(t, y’) = my’$
Then recast the form in terms of v:
$F(t, v) = mv’$
Let’s also recall that weight is:
$W=F=mg$
Motion Through a Resisting Medium Under Constant Gravitational Force:
In previous 2D motion physics problems our projectile motions were not inhibited by a resisting medium. Among the list of assumptions in these problems was that there was no effect due to water or air resistance (drag). This led to possible inaccuracies in the solutions in comparison to real world applications.
In order to attain a more accurate solution we will introduce resistive force as a parameter in our motion equation.
The total force acting on our object with the addition of a resistive force would be:
$F= -mg+F_{1}$
where $F_{1}$ is equal to a positive constant * velocity:
$F_{1}= k \lvert v \rvert =- kv$
this yields:
$mv’= -mg-kv$
rewrite in standard form for a first order linear equation and solve:
$v’+\frac{k}{m}v=-g$
Strategies:
When attempting to solve the differential equation consider:
- Are all units in the same system (CGS, MKS, British)?
- Recall that weight and mass are not the same.
- Mass = ?
- Acceleration due to gravity = ?
- k = ?
- Determine the general solution to the differential equation.
- Verify what the question is asking.
- Apply any additional parameters from the problem and solve the Initial Value Problem (IVP).
Escape Velocity:
Escape velocity is the speed that an object needs to be traveling to break free of a planet or moon’s gravity well and leave it without further propulsion (northwestern.edu).
- Time (t)
- Altitude (y, h), Maximum Altitude (ym)
- Escape Velocity (ve)
- Radius of Earth (R): 6378000m
- Gravitational Constant (G): 6.67 × 10-11 Newtons kg-2 m2
- Mass of the Earth (M)
Let $GM=K$
The gravitational force on the vehicle at an altitude $y$ above Earth is:
$F=-\frac{K}{(y+R)^2}$
Since $F=-mg$ when $y=0$ setting $y=0$ yields:
$-mg=-\frac{K}{R^2}$
and thus $K=mgR^2$:
$F=-\frac{mgR^2}{(y+R)^2}$
incorporate Newton’s second law of Motion formula:
$F=my”$ or $F=mv’$ or $F=ma$
therefore:
$a=\frac{gR^2}{(y+R)^2}$
or
$v’=\frac{gR^2}{(y+R)^2}$
When $t=0$ the velocity is $v_{0}$ and the altitude is $h$,
Therefore we can obtain $v$ as a function of $y$ by solving the initial value problem when $v(h) = v_{0} $. That is: when the altitude of the spacecraft is 0, it is on the surface (ie :its position is equal to the radius of the earth).
Note: $y+R$ is essentially distance from the center of the Earth. Where $y$ in this case is more accurately described as height above the surface, or altitude from the surface. Therefore $y+R$ yield $h$ which is position.
Integrate both sides:
$\frac{1}{2}v^2= \frac{gR^2}{h}+c$
Since $v(h) = v_{0}$, c equals:
$\frac{1}{2}v_{0}^2= \frac{gR^2}{0+R}+c$
simplify:
$\frac{1}{2}v_{0}^2= gR}+c$
solve for the constant of integration:
$c=\frac{1}{2}v_{0}^2-gR$
plug in $c$ to IVP yields:
$\frac{1}{2}v^2= \frac{gR^2}{h}+\frac{1}{2}v_{0}^2}-gR$
in terms of $v(h)$:
$v(h)=\sqrt{\frac{2gR^2}{h}+v_{0}^2-2gR$
When $\frac{1}{2}v_{0}^2-2gR>0$ the space vehicle has enough velocity to escape Earth.
in terms of $v_{0}$:
$v_{0}>\sqrt{2gR}$
Escape Velocity of Earth:
$v_{e}=\sqrt{2(9.8)(6378000)}=11.18\: m/s$
Escape Velocity Practical Exercise:
4.3.18: A space vehicle is to be launched from the moon, which has a radius of about 1080 miles. The acceleration due to gravity at the surface of the moon is about 5.31 ft/s . Find the escape velocity in miles/s.
Solution:
Radius of moon: $1080\:miles\rightarrow \frac{1\: mile}{5280\: feet}=5702400\:ft $
Gravity of moon: 5.31ft/s
$v_{e}=\sqrt{2(5.31)(5702400)}=7782\: ft/s=1.47 mi/s$
Examples of Applications:
Review the following examples in preparation for your practical exercise question:
__________________________________________________________________________
4.3.3: A boat weighs 64,000 lb. Its propellor produces a constant thrust of 50,000 lb and the water exerts a resistive force with magnitude proportional to the speed, with k D 2000 lb-s/ft. Assuming that the boat starts from rest, find its velocity as a function of time, and find its terminal velocity.
4.3.3 Solution
__________________________________________________________________________
4.3.5: A stone weighing 1/2 lb is thrown upward from an initial height of 5 ft with an initial speed of 32 ft/s. Air resistance is proportional to speed, with k = 1/128 lb-s/ft. Find the maximum height attained by the stone.
4.3.5 Solution
__________________________________________________________________________
4.3.7: A 96 lb weight is dropped from rest in a medium that exerts a resistive force with magnitude proportional to the speed. Find its velocity as a function of time if its terminal velocity is -128 ft/s.
4.3.7 Solution
__________________________________________________________________________
4.3.10: An object weighing 256 lb is dropped from rest in a medium that exerts a resistive force with magnitude proportional to the square of the speed. The magnitude of the resisting force is 1 lb when |v| = 4 ft/s. Find v for t > 0, and find its terminal velocity.
4.3.10 Solution
__________________________________________________________________________
Practical Exercise:
An object with mass m is given an initial velocity $v\_{0}\leq 0$ in a medium that exerts a resistive force with magnitude proportional to the square of the speed. Find the velocity of the object for $t > 0$, and find its terminal velocity.
Practical Exercise Solution:
$m\frac{dv}{dt}=mg-kv^2$
$\frac{dv}{dt}=g-\frac{k}{m}v^2$
$\int\frac{dv}{g-\frac{k}{m}v^2}=\int\ dt$
$\frac{-ln[\frac{\frac{k}{m}v-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v+\sqrt{\frac{gk}{m}}}]}{2\sqrt{\frac{gk}{m}}}=t+c$
$t=0; v=v_{0}; c=$
$\frac{-ln[\frac{\frac{k}{m}v_{0}-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v_{0}+\sqrt{\frac{gk}{m}}}]}{2\sqrt{\frac{gk}{m}}}$
$\frac{-ln[\frac{\frac{k}{m}v-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v+\sqrt{\frac{gk}{m}}}]}{2\sqrt{\frac{gk}{m}}}=t-\frac{-ln[\frac{\frac{k}{m}v_{0}-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v_{0}+\sqrt{\frac{gk}{m}}}]}{2\sqrt{\frac{gk}{m}}}$
$ln[\frac{\frac{k}{m}v-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v+\sqrt{\frac{gk}{m}}}]=-\beta t+ln[\frac{\frac{k}{m}v_{0}-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v_{0}+\sqrt{\frac{gk}{m}}}]$
$ln[\frac{\frac{k}{m}v-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v+\sqrt{\frac{gk}{m}}}*\frac{\frac{k}{m}v_{0}-\sqrt{\frac{gk}{m}}}{\frac{k}{m}v_{0}+\sqrt{\frac{gk}{m}}}]=e-\beta t$
$v=\alpha \frac{v_{0}(1+e^-\beta t)-\alpha(1-e^-\beta t)}{\alpha(1+e^-\beta t)-v_{0}(1-e^-\beta t)}$
where:
$\alpha = \sqrt{\frac{mg}{k}$ and $\beta = 2\sqrt{\frac{kg}{m}}$
$v_{t}={t\to\infty}; {e^-\beta t\to}0$
$v_{t}=\alpha\frac{v_{0}-\alpha}{\alpha-v_{0}}=-\alpha(\frac{v_{0}-\alpha}{v{0}-\alpha})=-\alpha$




Leave a Reply