Section 6.3, Question 3
Find the current (I) in the RLC circuit, assuming that E(t) = 0 for t>0.
R = 2 ohms, L = 0.1 henrys, C = 0.01 farads,$ Q_o$ = 2 coulombs, $I_o$ = 0 amperes
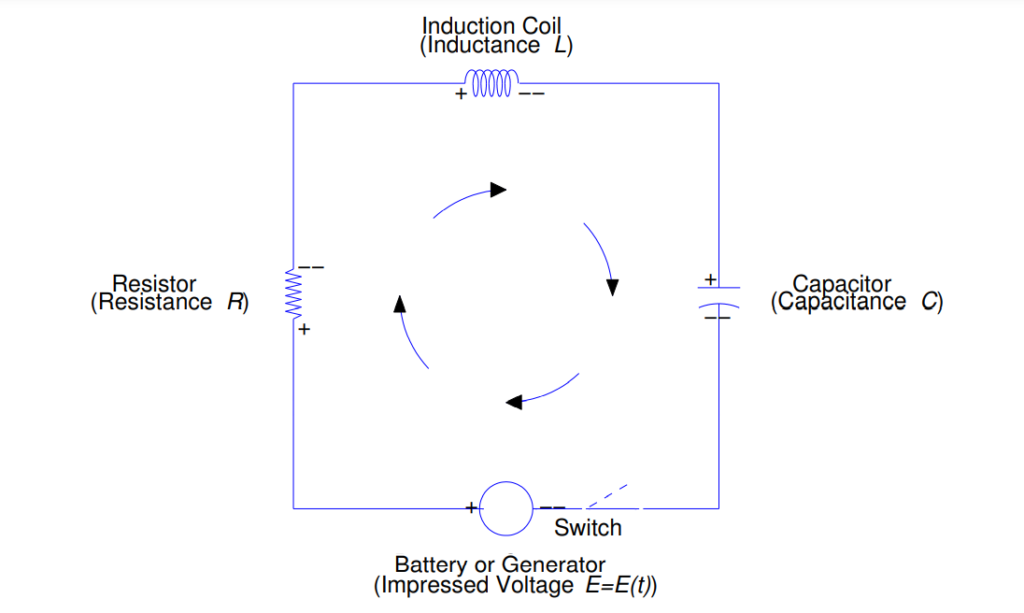
According to Kirchhoff’s Law the sum of the voltage drops in a closed RLC circuit is equal to the impressed voltage E(t).
L$I’$ + RI + $\frac{1}{C}$Q = E(t)
This equation can be rewritten by replacing I with Q’ because charge stored in a capacitor is related to the current according to the equation below:
Q = $Q_o$ + $\int_{0}^{t}$ I($\tau$) d$\tau$
Rewritten Equation:
L$Q”$ + R$Q’$ + $\frac{1}{C}$ = E(t)
Substituting the values of L, R, C, and E(t) we get:
0.1 $Q”$ + 2 $Q’$ + $\frac{1}{0.01}$ Q = 0
0.1 $Q”$ + 2 $Q’$ + 100 Q = 0
Characteristic Equation:
0.1 $r^2$ + 2r + 100 = 0
Use the quadratic formula to find roots.
r = $\frac{(-2)\pm\sqrt{2^2-4(0.1)(100)}}{2(0.1)}$
= $\frac{-2\pm\sqrt{-36}}{0.2}$
= $\frac{-2\pm6i}{0.2}$
r = $-10\pm30i$
$r_1$ = $-10 + 30i$, $r_2$ = $-10-30i$
Roots are complex so general solution is:
y=$e^{\lambda x}$[$C_1$cos($\omega x$) + $C_2$sin($\omega x$)]
$\lambda$ = (-10), $\omega$ = (30) based on the roots we found
so;
Q(t) = $e^{-10t}$[$C_1$cos(30t)+$C_2$sin(30t)]
with $Q_o$=Q(0)=2 coulombs when t=0 we can solve for constant $C_1$
Q(0)=$e^{-10(0)}$[$C_1$cos(30 $\times$ 0)+$C_2$sin(30 $\times$ 0)]
cos(0)=1, sin(0)=0
2 = 1[$C_1$$\times$1+0]
2 = $C_1$
$I_o$=0 amperes : $I_o$=$Q’_o$=0 we use this to solve for constant $C_2$ and t=0
Q(t) = $e^{-10t}$[$C_1$cos(30t)+$C_2$sin(30t)]
$\frac{d}{dt}$Q(t) = ($e^{-10t}$[$C_1$cos(30t)+$C_2$sin(30t)]) $\frac{d}{dt}$
$Q'(t)$=[-10$C_1$ $e^{-10t}$ cos(30t) – 30$C_1$ $e^{-10t}$ sin(30t)] + [-10$C_2$ $e^{-10t}$ sin(30t) + 30$C_2$ $e^{-10t}$ cos(30t)]
0 = [-10$\times$ 2 $e^{-10(0)}$ cos(30$ \times 0$) – 30 $\times$ 2 $e^{-10(0)}$ sin(30$\times$ 0)] + [-10$C_2$ $e^{-10(0)}$ sin(30$\times$ 0) + 30$C_2$ $e^{-10(0)}$ cos(30$\times$ 0)]
0 = -20 + 0 + 0 + 30$C_2$
20 = 30$C_2$
$\frac{2}{3}$ = $C_2$
Therefore:
Q(t) = 2$e^{-10t}$cos(30t) + $\frac{2}{3}$ $e^{-10t}$sin(30t)
We differentiate Q(t) to get the current (I).
$\frac{d}{dt}$Q(t) = [2$e^{-10t}$cos(30t) + $\frac{2}{3}$ $e^{-10t}$sin(30t)]$\frac{d}{dt}$
$Q'(t)$ = I = -20$e^{-10t}$cos(30t) – 60$e^{-10t}$sin(30t) – $\frac{20}{3}$ $e^{-10t}$sin(30t) + 20$e^{-10t}$cos(30t)
I = $\frac{-200}{3}$ $e^{-10t}$sin(30t)







Recent Comments