Section 1.2 and 1.3 — Brian E.

Practice Problem 1.2.2.E

Verify that the given is a solution to the ODE:

$y = \tan(\frac{x^{3}}{3}+c); y’ = x^{2}(1+y^{2})$

Solution:

$\frac{d}{dx}(\tan(\frac{x^{3}}{3}+c)) = x^{2}\sec^{2}(x)$

Recall that ,

$\tan^{2}(\theta)+1 = \sec^{2}(\theta)$

Thus,

$(1+y^{2}) = (1+tan^{2}(\frac{x^{3}}{3}+c)) = \sec^{2}(\frac{x^{3}}{3}+c))$

Therfore,

$y’ = x^{2}(1+y^{2}) = x^{2}(1+tan^{2}(\frac{x^{3}}{3}+c)) = x^{2}\sec^{2}(x)$

$y$ is a solution for $y’$ for all all real numbers ($\mathbb{R}$) excluding when $\frac{x^{3}}{3}+c = 0$

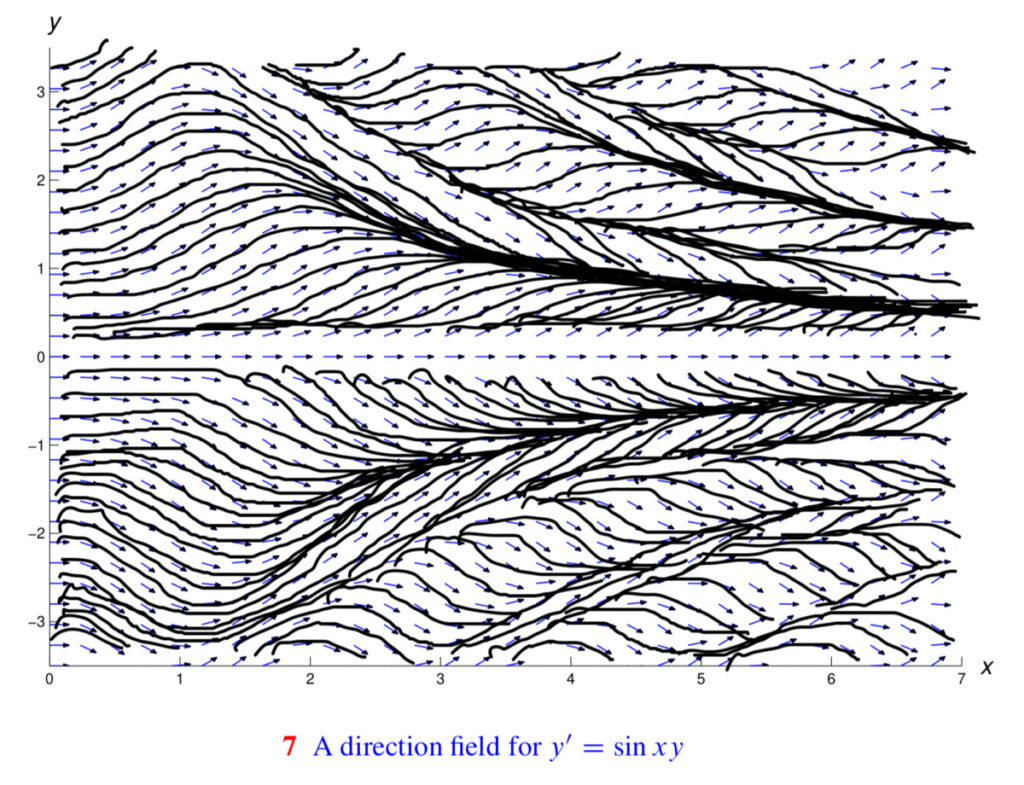
Practice Problem 1.3.7