Hi everyone! This online lesson is provided as a resource – we will also go over this material in class.

Lesson 4: Indexed Sets

Topic. This lesson covers:

  • Sec 1.8: Indexed Sets

Learning Outcomes.

  • Take unions and intersections of collections of sets indexed by the natural numbers or other sets.

Homework. There is 1 written assignment on today’s material:

  1. Homework: Section 1.8 p.29: 3, 5, 6, 8

Lecture Notes:

Lesson-4_-Indexed-SetsDownload

Vocabulary

  • indices
  • indexed sets
  • index set I

Indexed Sets

Introduction

When we need to talk about a lot of different sets, instead of giving each of them different names A, B, C, D, E, F it’s convenient to keep track of them by using subscript numbers, like A_{1}, A_{2}, A_{3}, A_{4}, A_{5}. The subscript numbers are called indexes (“indices”), and the sets are called indexed sets. 

Definitions and Theorems

  • Indexed sets are sets that are distinguished by attaching subscript numbers (instead of using different letters), such as A_{1}, A_{2}, A_{3}, A_{4}, A_{5}. We call the number 1,2,3,4 and 5 the indices.
  • Unions and intersections of many sets. Suppose A_{1}, A_{2}, A_{3}, \ldots, A_{n} are sets. Then
    • A_{1} \cup A_{2} \cup A_{3} \cup \ldots \cup A_{n}=\left\{x: x \in A_{i}\text{ for at least one set } A_{i}, \text{ for }1 \leq i \leq n\right\}
    • A_{1} \cap A_{2} \cap A_{3} \cap \ldots \cap A_{n}=\left\{x: x \in A_{i} \text{ for every set } A_{i}, \text{ for } 1 \leq i \leq n\right\}
  • Notation. Given sets A_{1}, A_{2}, A_{3}, \ldots, A_{n}, we define

        \[\bigcup_{i=1}^{n} A_{i}=A_{1} \cup A_{2} \cup A_{3} \cup \ldots \cup A_{n} \text{ and }\]


        \[\bigcap_{i=1}^{n} A_{i}=A_{1} \cap A_{2} \cap A_{3} \cap \ldots \cap A_{n}\]

  • Definition. The index set I is the set of all indices (of a collection of sets).
  • Notation. If I is an index set, and for each \alpha \in I we have a corresponding set A_{\alpha}, then
    • \bigcup_{\alpha \in I} A_{\alpha}=\left\{x: x \in A_{\alpha}\text{ for at least one set } A_{\alpha} \text{ with }\alpha \in I\right\}
    • \bigcap_{\alpha \in I} A_{\alpha}=\left\{x: x \in A_{\alpha}\text{ for every set } A_{\alpha} \text{ with }\alpha \in I\right\}

Examples: Indexed Sets

Example 1: Suppose A_{1}=\{0,2,5\}, A_{2}=\{1,2,5\} and A_{3}=\{2,5,7\}.
Find \bigcup_{i=1}^{3} A_{i} \text { and } \bigcap_{i=1}^{3} A_{i}

VIDEO: Introduction to Indexed Sets, Example 1

Example 2: Consider the following infinite list of sets:

    \[A_{1}={-1,0,1}, A_{2}={-2,0,2}, A_{3}={-3,0,3}, \ldots, A_{i}={-i, 0, i}, \ldots\]


Find \bigcup A_{i} \text { and } \bigcap_{i=1}^{\infty} A_{i}

VIDEO: Indexed Sets – Example 2

Example 3: Let the index set I be the interval [4,5), that is I=[4,5)]=\{x: 4 \leq x<5\}. For each number \alpha \in I, let the set A_{\alpha}=\{x \in \mathbb{R}: \alpha \leq x \leq 6\}.

    \[\text { Find } \bigcup_{\alpha \in[4,5)} A_{\alpha} \text { and } \bigcap_{\alpha \in[4,5)} A_{\alpha}\]

VIDEO: Indexed Sets – Example 3

Introduction to Logic

The word logic refers to the way that humans reason – how we combine old information to deduce new information.  It is nothing exotic – you use logic all the time in your everyday life, and certainly when you do mathematics.  In Chapter 2, we will be looking at this familiar tool and studying its rules.

VIDEO: Introduction to Logic

Exit Question

Let the index set I be the closed interval [0,2], that is I=[0,2]=\{x: 0 \leq x \leq 2\}. For each number \alpha \in I, let the set A_{\alpha}=\{(x, \alpha): x \in \mathbb{R}, 1 \leq x \leq 2\}.

    \[\text{ Find } \bigcup_{\alpha \in[0,2]} A_{\alpha} \text { and } \bigcap_{\alpha \in[0,2]} A_{\alpha}\]

Answer

\bigcup_{\alpha \in[0,2]} A_{\alpha}=\{(x,y)\in\mathbb{R}^2 : 1\leq x\leq 2, 0\leq y\leq 2\} (shown in red in the image below). Why do the x-values range from 1 to 2 but y-values range from 0 to 2?

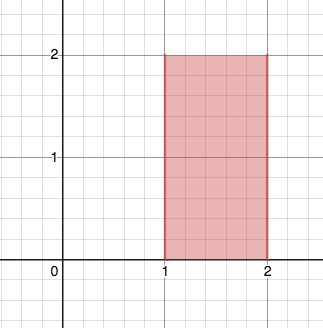
graph showing shaded region representing the union of A_alpha.

\bigcap_{\alpha \in[0,2]} A_{\alpha} = \emptyset. Why is this?