Monthly Archives: November 2017

Wednesday 29 November class

Apologies for the delayed posts while I was getting my computer fixed… I’m working on catching up now

Topics:

• Discussion of finding intervals of convergence for power series. The solutions to the quiz are posted here.

• Important Taylor series that you should recognize when you see them. See the list below.

• Using known Taylor series to get new Taylor series, by multiplying by a polynomial or substituting a polynomial in place of x.

• New topic: finding the area between two curves (just an introduction).

These are true areas, not the kind of “area” we get from the definite integral, which could be positive or negative. Therefore we have to make sure and look at the graph to get the subtraction in the correct order, so the result will be positive (and no piece of it will be negative).

 

Important Taylor series: (see more in Key Idea 32 on p.482, but I’ve changed the list a bit)

Make sure that you also know or can easily figure out the intervals of convergence!

e^{x} = \displaystyle \sum_{n=0}^{\infty}\frac{x^{n}}{n!}

 

\sin(x) = \displaystyle \sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n+1}}{(2n+1)!}

 

\cos(x) = \displaystyle \sum_{n=0}^{\infty}\frac{(-1)^{n}x^{2n}}{(2n)!}

 

\ln(x) = \displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}(x-1)^{n}}{n}

 

\ln(1+x) = \displaystyle \sum_{n=1}^{\infty}\frac{(-1)^{n+1}x^{n}}{n} * not in textbook

 

\frac{1}{1+x} = \displaystyle \sum_{n=0}^{\infty}x^{n} (Geometric series)

 

Apologies for the “Formula does not parse” error below: the formula is correct, but WordPress is not interpreting it for some reason. Please look for the formula for the inverse tangent in the textbook (or elsewhere).

 

 

Homework:

• Review the examples discussed in class. A good way to familiarize yourself with the important Taylor series is to find them from scratch a few times. The arctangent formula is probably the most difficult (because you must repeatedly use the quotient rule).

• Finish the WeBWorK on Taylor series, and try a little of the areas between curves. Please do not wait to the last minute! In case the problem asks just for the area bounded between two curves, but does not tell you where to start and end the integral, you have to figure out where the two curves intersect. Using Desmos may help with this.

• There will be a quiz next time: the topic will be using known Taylor series to give new ones, and finding intervals of convergence for Taylor series.

• Don’t forget that Test 4 is scheduled for next Wednesday. The review self-tests will be in a separate post. This will be a shorter test than usual, so I will add to it a “makeup” problem similar to one that was commonly missed on a previous test. Make sure you look for it. This will give you an opportunity to improve a previous test score.

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

Monday 27 November class

Topics:

• Discussion of some problems finding radius and interval of convergence for power series.

Note: it is important to be aware of which test you are using (so that you carry it out correctly) and that you write your work in a logical way. Know what you are doing and what it is supposed to accomplish at each step.

Also we are using the fact that |x-c| < R translates into -R < x-c < R. There are other ways to handle absolute value inequalities, but since this is the only type of absolute value inequality we will need in this class and we want to get the interval of convergence, this is the best and most direct way to do it.

 

• Taylor series (introduction)

A Taylor series is just an infinite Taylor polynomial. Notice that this means that the function must have infinitely many derivatives, which is not always the case. (This may limit the interval of convergence.)

A taylor series being a power series, it will have a radius and interval of convergence. There is also the question of exactly what it converges to, if the series converges. There is a way to prove that the Taylor series converges to the original function, using the remainder theorem for Taylor polynomials, which works in many cases.

We will assume that for the Taylor series we discuss in this class, they converge to the original function inside the radius of convergence. (Problems can happen at the endpoints of the interval of convergence.)

The simplest and maybe most beautiful example of a Taylor series is the Maclaurin series for e^{x}, which we found in class

1 + x + frac{x^{2}}{2} + \frac{x^{3}}{3!} + \frac{x^{4}}{4!} + \dots = \displaystyle\sum_{n=0}^{\infty}\frac{x^{n}}{n!}

We showed using the Ratio Test that this converges on the whole real line. (It is also possible to prove that what it converges to is the function e^{x})

 

Another example: the Taylor series for \ln(x) centered at x=2. (Note that \ln(x) does not have a Taylor series around x=0, since \ln(0) is undefined. So any Taylor series for \ln(x) must be centered around some x-value where the natural logarithm is defined.)

This example is worked out in Paul’s Online notes.(Example 7)  It turns out to give this:

\ln(2) + \displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n+1}{n2^{n}}(x-2)^{n}

There are two more commonly used Taylor Series for the natural logarithm, which are Maclaurin series for \ln(1-x) and \ln(1+x). Using the series for \ln(1+x) we can prove that the alternating harmonic series converges to \ln(2), by substituting x=1 into that series. (We should first prove that the interval of convergence includes x=1, of course!)

There are important Taylor series that are commonly used and that you should become familiar with. We will make a list of some of them next time.

 

Homework:

• Review the examples discussed in class. Make sure that you understand how we are implementing the various tests for convergence at each step.

• Review how to find Taylor polynomials if you need to do so.

There is a series of videos and practice problems on Khan Academy if you are interested. (The iink is to the first video in the series.)

• Do the WeBWorK: please do not wait to the last minute! The WeBWorK on Power Series is due Tuesday evening. The WeBWorK on Taylor series is not due until Sunday, but again, please do not wait, and make sure to post questions on Piazza if you encounter difficulty.

• I have posted two problems on Piazza which may be done (in Piazza) for extra credit. These are intended to be used ONLY by people who have  not yet had a chance to put a problem on the board in class: please respect this, and also please only do ONE problem if you choose to do so. I may post more problems from time to time, so make sure you are getting alerts from Piazza. (On a computer, you can go into your account/email settings and check how you are being notified and make changes, if necessary.)

• It would be a good idea to fill out the ThinkingStrategicallyPreTestSurvey at this point to start preparing for Test 4!

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Monday 20 November class

Topics:

• Discussion of some homework problems, including estimating the sum of a convergent alternating series

• The Root test for absolute convergence

• Power series: definitions and vocabulary

A power series centered at a is a series which has the form \displaystyle\sum_{n=0}^{\infty}c_{n}(x-a)^{n}, where the c_{n} are real numbers called the coefficients of the series. Note that (as usual) the sum does not have to start at n=0. It starts wherever it starts. (Note also the similarity to Taylor polynomials!)

The series may or may not converge for various values of the variable x. If the series converges at all, there is a non-negative number R (possibly infinity) such that:

If |x-a| < R the series converges absolutely,

If |x-a|>R the series diverges.

R is called the radius of convergence of the power series.

Note that if |x-a| = R, the series may either converge or diverge. We have to look more closely to see what happens then.

This all should remind you of what happens when we use the Ratio (or Root) tests for absolute convergence. The Ratio Test will be our main tool for analyzing power series and their convergence. (We will have to use all of our other tests to determine what happens at the endpoints where the limit is 1 from that test, though.)

 

Example: \displaystyle\sum_{n=1}^{\infty}\frac{(-1)^{n}n}{4^{n}}(x+3)^{n}

This is a power series centered at -3. Let’s find the radius of convergence using the Ratio Test!

We can forget about the powers of -1, since we are taking absolute values

\left|\frac{a_{n+1}}{a_{n}}\right| = \frac{\frac{n+1}{4^{n+1}}|(x+3)^{n+1}|}{\frac{n}{4^{n}}|(x+3)^{n}|} = \frac{n+1}{4n}|x+3|

 

\displaystyle\lim_{n\rightarrow\infty}\frac{n+1}{4n}|x+3| = \frac{1}{4}|x+3|

So the power series will converge (absolutely) if $latex \frac{1}{4}|x+3| <1$, in other words it will converge absolutely if |x+3| <4, and it will diverge if |x+3| >4: so the radius of converge is 4, according to the definition given above.

We would have to to look more closely using other tools to find out whether or not the series converges when |x+3| =4. We will do that next time.

 

 

 

 

 

Some notes from class:

Here is a version of problem 11 from the WeBWorK Ratio and Root Tests, which was partially worked out in class.

The problem was to use the root test on the series \displaystyle\sum_{n=1}^{\infty}\left(1+\frac{1}{5n}\right)^{-n^{2}} , which resulted in our having to find the limit

\displaystyle \lim_{n\rightarrow\infty}\left(\left(1 + \frac{1}{5n}\right)^{-n^{2}}\right)^{\frac{1}{n}} = \lim_{n\rightarrow\infty}\left(1 + \frac{1}{5n}\right)^{-n}

I rewrote that to simplify it somewhat:

\displaystyle \lim_{n\rightarrow\infty}\left(1 + \frac{1}{5n}\right)^{-n} =\lim_{n\rightarrow\infty}\left(\frac{5n+1}{5n}\right)^{-n} = \lim_{n\rightarrow\infty}\left(\frac{5n}{5n+1}\right)^{n}

You will need to use L’Hopital’s Rule to find that limit, since it has the indefinite form 1^{\infty}

Here is the basic procedure:

Let y = \displaystyle\lim_{n\rightarrow\infty}\left(\frac{5n}{5n+1}\right)^{n}.

To change this problem into one that will have a simpler indefinite type, take the logarithm:

\ln(y) = \displaystyle\ln\left(\lim_{n\rightarrow\infty}\left(\frac{5n}{5n+1}\right)^{n}\right) =\lim_{n\rightarrow\infty}\ln\left(\frac{5n}{5n+1}\right)^{n} since the logarithm is a continuous function.

You would then use the “log of a power” rule to turn this into a limit which has the form \infty\cdot 0, and then do a rewrite to get the form \frac{0}{0}. I have given up on trying to type in the rest of the procedure here, as WordPress will not display it correctly. Please see the note posted on Piazza for the rest of this.

If you want to see an example worked out for the indefinite form $latex 1^{\infty}$, see Example 192(1) on p. 329 of the textbook. (This is the limit which is sometimes used to define e, and you may be able to find it online as well, but why bother since it is in your text?)

One of the problems in that WeBWorK involved factorials. For simplifying quotients of factorials, you just have to remember how they are defined. Here is the example I discussed:

\frac{(2n+1)!}{(2n+3)!} = \frac{(2n+1)!}{(2n+3)(2n+2)(2n+1)\cdots(1)} = \frac{(2n+1)!}{(2n+3)(2n+2)(2n+1)!} =\frac{1}{(2n+3)(2n+2)}

When you have to simplify a quotient of factorials, always expand them out (at least in your mind) to see how they can be reduced.

 

Homework:

• Review the examples and definitions discussed in class. Make sure that you understand what a power series and the radius of convergence for a power series are.

• Finish the WeBWorK “Ratio and Root Tests”. You do not need to work on the Power Series WeBWorK yet: you can look at it if you like.

• Here is a video from PatrickJMT showing how to find the interval of convergence for a power series in the simplest case, where the center is at 0. The new thing is how to determine whether or not the endpoints of the interval (where the limit of the ratio test is 1) are to be included in the interval of convergence or not. We have to use one of the earlier tests about convergence of series to figure this out separately for each endpoint. We will go into this in more depth next time. Also, on to Taylor Series.

• There will be a quiz next time. The topics will be the alternating series test, and the ratio and root tests.

• Don’t forget to fill out the Post-Test Strategic thinking survey: research has shown that using this type of survey and thinking about your use of resources significantly improves test scores!

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Wednesday 15 November class (Updated)

(After Test 3)

Reminder: we have a theorem about series that says: if \displaystyle\sum a_{n} converges, then \displaystyle\lim_{n\rightarrow\infty}a_{n} = 0.

So if \displaystyle\lim_{n\rightarrow\infty}a_{n} \neq 0, the series will diverge!

 

Reminder: the Integral Comparison, Direct Comparison , and Limit Comparison tests ONLY apply to series whose terms are all positive. They cannot be used on alternating series or series which have an infinite number of negative terms.

 

Absolute convergence: a series \displaystyle\sum a_{n} converges absolutely (is absolutely convergent) iff the series \displaystyle\sum|a_{n}| converges.

 

If \displaystyle\sum a_{n} converges, but \displaystyle\sum|a_{n}| diverges, we say the series is conditionally convergent.

 

Theorem: If the series is absolutely convergent, then it is conditionally convergent.

(But not the converse!)

 

Examples:

\displaystyle\sum_{n=1}^{\infty} (-1)^{n+1}\frac{1}{n} is not absolutely convergent. It is only conditionally convergent.

 

\displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}|\sin(n)|}{n^{2}} is absolutely convergent:

\displaystyle\sum_{n=1}^{\infty} \frac{|\sin(n)|}{n^{2}} converges by comparison with the p-series with p=2.

Since \displaystyle\sum_{n=1}^{\infty} \frac{(-1)^{n+1}|\sin(n)|}{n^{2}} is absolutely convergent, it converges (conditionally) as well.

 

\displaystyle\sum_{n=1}^{\infty} \frac{\sin(n)}{n^{3}} (not an alternating series) – no possibility of using the alternating series test here.

But \displaystyle\sum_{n=1}^{\infty} \frac{|\sin(n)|}{n^{3}} converges. so \displaystyle\sum_{n=1}^{\infty} \frac{\sin(n)}{n^{3}} converges absolutely, and also (therefore) converges conditionally.

 

Ratio/Root tests slideshow

MAT1575Ratio-RootTests-slideshow

Example: (My version of Problem 1 in the WeBWorK)

Consider the series \displaystyle\sum_{n=1}^{\infty}\frac{10^{n}}{(n+1)4^{2n+1}}

Evaluate the limit

\displaystyle\lim_{n\rightarrow\infty}\left|\frac{a_{n+1}}{a_{n}}\right|

I’ve worked this out in a separate pdf, because WordPress will not display it correctly for unknown reasons.

MAT1575WeBWorKRatioTestProblem1

 

Homework:

• Review the examples discussed in class (most of the notes are above). Make sure that you know when you can and cannot use the comparison tests (which are generally the easiest to use in the cases when they can be used).

• Do/finish the WeBWorK on Alternating Series and do the WeBWorK on the Ratio Test and Root test, but skip the problems #7, 9, 10, 11, and 14 (which refer to the root test) for now.

Note: None of the problems in the Alternating Series homework require the ratio or root tests, even the ones that ask about absolute convergence. You should try to use the Alternating Series test to test for convergence: if the problem asks about absolute convergence, try using one of the comparison tests on the series of absolute values.

Also, for the questions about estimation, you will be using the theorem from last time about the error term. Here are some videos also about this:

PatrickJMT Alternating Series Estimation Theorem

Khan Academy

• I would like to see some of the Alternating Series and Ratio Test problems on the board next time.

• No quiz next class.

• The Test 3 solutions and Post-Test strategic thinking survey are in this separate post. It is very valuable to fill out the post-test survey even if you did not fill out the pre-test survey!

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Test 3 solutions and post-test strategic thinking survery

Here is the Thinking Strategically Post-Test Survey: it will be useful for you to complete this even if you did not complete the pre-test survey (as it will help with your future test preparation)

ThinkingStrategicallyPostTestSurvey

 

Here are the solutions to the problems on Test 3. Please let me know if you find any typos or other errors in these!

UPDATE: errors in the answers to #3a and 3c have been corrected in this new version. (My answer key that I used for grading had the correct answers: these were typos or copy-paste errors that sneaked into the typed version.)

MAT1575Test3-solutions

Monday 13 November class

 

I apologize for the “Formula does not parse” and the failure to interpret latex errors below, which are occurring due to glitches in WordPress and I cannot figure out how to make them go away. I want to post this without further delay anyway.

Topics:

• two “distributed practice” review problems:

Determine whether the series converges or diverges, and find the sum if it converges: 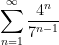\displaystyle\sum_{n=1}^{\infty}\frac{4^{n}}{7^{n-1}}

Find the 4th degree Maclaurin polynomial for f(x) = \sqrt{x+1}

• New topic: Alternating series, the alternating series test for convergence, and estimating sums of alternating series.

Note: we are doing the topics in a different order than the order they are listed on the Course Outline (and in the textbook) because the Ratio and the Root tests are really tests for absolute convergence, and it seems better to introduce them only after we have studied absolute convergence.

 

Alternating series are simply series where consecutive terms have alternating signs. We have already seen examples of this. There are two very common ways to write alternating series, namely, if \{b_{n}\} is a positive sequence, we can write an alternating series as either

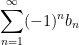\displaystyle\sum_{n=1}^{\infty}(-1)^{n}b_{n} — this will make the first term have a negative sign and the second term have a positive sign, and so on

or we can write

\displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}b_{n} — this will make the first term have a positive sign and the second term have a negative sign, and so on.

The second version is more common. The point is that when you see a series written in this kind of way, with a (-1) to the n, n+1, or even n-1 power included, you should recognize that it is an alternating series.

 

The alternating series test: For an alternating series, if the absolute values of the terms form a sequence which is decreasing and whose limit is 0, then the alternating series converges.

Note: there are two conditions that must be checked in order to use this theorem. Also, it cannot tell if the series diverges: it can only sometimes tell you that the series converges. If either of the two conditions fails, you must use some other test.

 

Examples:

The alternating harmonic series 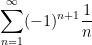\displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}\frac{1}{n} converges, because the absolute values of the terms are

1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}, \dots

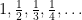
and this sequence is clearly decreasing and its limit is 0. So the alternating harmonic series converges. This does not tell us what it converges to: in fact, the sum is 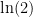\ln(2) as we will show later.

(So even though the harmonic series diverges, the alternating harmonic series converges. Keep this in mind when we get to absolute convergence.)

 

Now consider the alternating series 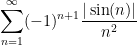\displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}\frac{|\sin(n)|}{n^{2}}. (We suspect this converges: do you see why?)

Can we use the alternating series test on this? The absolute values of the terms have the form $latex \frac{|\sin(n)|}{n^{2}}$, namely they form the sequence

These do not form a decreasing sequence, as we can see by looking at the graph:

Remember we are only interested in the points where the x-value is a natural number: but even for those (I have marked off the first few of them) they are not decreasing and it is not clear that even if we go far out in the graph they will ever form a decreasing sequence. So we cannot use the absolute value test for this alternating series: we will have to use some other test (and we will do so!)

 

Now consider the alternating series \displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}\frac{\ln(n)}{n} Can we use the alternating series test?

The absolute values of the terms have the form $latex \frac{\ln(n)}{n} = 0, \frac{\ln(2)}{2}, \frac{\ln(3)}{3}, \dots$

We suspect that they form a decreasing sequence, at least eventually, because the denominator is growing faster than the numerator. By looking at the graph, we can see that they do start to decrease but not right away: they seem to start decreasing at some point after n=2.

(In fact, you can show by using the derivative of 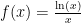f(x)= \frac{\ln(x)}{x} that the maximum occurs at 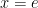x=e, so the terms will in fact be decreasing starting with n=3. And you should do this! It is not good to put too much trust in graphs alone. I’ve marked that maximum point on the graph linked above.)

So the sequence of absolute values is decreasing from n=3 onward. It is always OK when determining convergence if we ignore the first few terms of a series: convergence is determined by what happens “in the long run”.

Also, 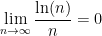\displaystyle\lim_{n\rightarrow\infty}\frac{\ln(n)}{n} = 0, so the second condition holds.

Therefore the alternating series \displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}\frac{\ln(n)}{n} converges. (Although we don’t know what it converges to!)

 

We have seen several times that we can know that a series converges without being able to know what it converges to. There is a theorem that tells us how good an alternating series’ partial sums are at estimating the sum of the series.

Estimating sums of convergent alternating series:

Suppose that 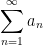\displaystyle\sum_{n=1}^{\infty}a_{n} is a convergent alternating series whose sum is L,:

L = \displaystyle\sum_{n=1}^{\infty}a_{n}

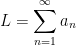
We want to estimate L by using the partial sum $S_{n}$.

Then the error we would make would be less than 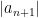|a_{n+1}| in size: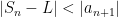 |S_{n}-L|<|a_{n+1}|

And we also know that the true sum L is between 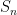S_{n} and S_{n+1}:

S_{n} < L < S_{n+1}

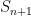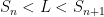
Using this theorem and the alternating harmonic series, suppose we wanted to estimate the sum of the alternating harmonic series (which we have said, but not proved, is 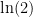\ln(2)) to within 1/5. (In other words, we want our estimate to be no more than 1/5 = 0.2 away from the true value.)

Since 1/5 is the absolute value of the 5th term of the series, we will estimate by S_{4} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} = \frac{7}{12} \approx 0.583.

The theorem tells us that this estimate is no more than 0.2 off from the true value of the sum of the series (which is 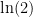\ln(2), and also that the true value of the series is in between this number and S_{5} = \frac{7}{12} +\frac{1}{5} = \frac{47}{60} \approx 0.783.

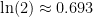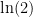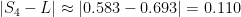In fact, \ln(2)\approx 0.693, so it is between  0.583 and 0.783, and the error we would make using 0.583 as an estimate for \ln(2) is |S_{4}-L| \approx |0.583 - 0.693| = 0.110 which is indeed less than 0.2.

 

Homework:

• Review the examples discussed in class (which are mostly detailed above).

• Also recommended: Paul’s Online Notes on Alternating series and the alternating series test.

Note: make sure that you understand when and how to use the alternating series test. We are not using the Ratio Test yet: please don’t try to bypass what we are doing right now, it will only harm you in the long run.

• You may also want to look at Paul’s Online notes for estimating alternating series: it is about halfway down in these notes.

And here is PatrickJMT on estimating alternating series

• Do at least the following problems from the WeBWorK on Alternating Series: #1-4 and #9. Note that in some problems you only get one attempt, so make it count! Also note that in problems 2 and 3 you are only to make use of the alternating series test, not some other test you may happen to know.

• Don’t forget that Test 3 is scheduled for Wednesday. Review materials are in this separate post.

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Test 3 review materials

Test 3 is scheduled for Wednesday 15 November, the first hour or so of class.

Here is the survey for you to use to plan how to make best use of the resources available to you: this is for your private use

ThinkingStrategicallyPreTestSurvey

Here are the review self-tests, with some errors corrected: notably, problem 2 should have referred to “sequences”, not series, and that has been fixed.

MAT1575Test3Review

Here are the answers, with extensive hints and partial solutions for the first Self-Test: less detail is given for the second self-test

MAT1575Test3ReviewAnswersFall2017

 

Please let me know if you find any errors in these!

 

Here are links to some additional resources:

On Taylor Polynomials:

Video from PatrickJMT (on YouTube, so may autoplay another video after)

Taylor Polynomial Ex. 1

Taylor Polynomial Ex. 2

Paul’s Online Math Notes on special series (geometric and telescoping, mainly)

 

Wednesday 8 November class

Topics:

• Theorems about convergence/divergence of series

So far we have the following:

• The integral convergence test (from last time):

• (Direct) Comparison test: this is very similar to the direct comparison test for improper integrals where the upper bound of integration is infinite.

• Limit Comparison test: this is also very similar to the limit comparison test for improper integrals where the upper bound of integration is infinite.

Strategy to choose a method: I would usually try them in the order given above. If it is easy to do integral test, use that. (Maning, you can easily figure out whether the integral converges or diverges.) If that is not easy, see if there is a direct comparison with some series you know about (a geometric or p-series, especially). If the direct comparison does not work because the inequality goes the wrong way, it is very likely that you can use limit comparison.

I worked these examples using the integral test:

The harmonic series \sum_{n=1}^{\infty}\frac{1}{n} diverges, because we can compare to the integral \int_{1}^{\infty} \frac{1}{x}\textrm{d}x and we show (or remember) that this diverges.

Note: the harmonic series is just a p-series with p=1. Similarly, we can show that any p-series will converge if p>1 and diverge if p\le 1, by comparing to the appropriate improper integral.

 

Show that \sum_{n=0}^{\infty} ne^{-n^{2}} converges: this example will show you a couple of important considerations in using the integral convergence test which you may be tempted to skip over, so study it carefully.

Unfortunately, the LaTeX rendering in WordPress is being very glitchy so I cannot just type this example in this post. I have made it in pdf form for you:

MAT1575IntegralConvergenceTestExample

You can also find a discussion of this example in Paul’s Online Math Notes. (example 2 on that page)

Here are some links to relevant parts of Paul’s notes:

Integral test notes

Integral test practice problems

Comparison test and Limit comparison test notes

Comparison test and Limit comparison test practice problems

It’s very good to use those practice problems to test yourself, as you can see his solutions right away when you finish. Testing yourself is one of the best ways to learn.

Homework:

• Review the examples discussed in class for all 3 of these tests. You can (and should!) also look at Paul’s Online Math Notes for even more examples and practice problems.

• Do the WeBWorK assignments on Intro to Series 2 (which has been extended) and Comparison Tests. Another assignment was also posted but you do not need to work on it yet.

• Don’t forget that Test 3 is scheduled for next Wednesday. The review materials will be in a separate post.

 

 

Don’t forget, if you get stuck on a problem, you can post a question on Piazza. Make sure to give your question a good subject line and tell us the problem itself – we need this information in order to answer your question. And please only put one problem per posted question!

 

Test 2 solutions and redo problems (bumped up to top of posts)

Here are the solutions to Test 2, according to the version you have (look at the lower left on the cover sheet)

MAT1575Test2a-solutions    version \alpha

MAT1575Test2b-solutions   version \beta

Here are some errors that were frequently made, which I did not mention in those solutions:

• The integral \int \frac{\textrm{d}x}{x} is \ln|x| + C: the absolute value signs are essential! Too many people left them out. This can cause you to think a definite integral doesn’t converge when it really does. Be careful!

• The definitions of the improper integrals where there is a singularity of the integrand (the range is unbounded) involve one-sided limits: it is important to take the correct limit, because the two one-sided limits may not agree with each other and it is possible that one of them exists and the other does not. Please look at the definition given in the textbook on p. 337 (Definition 25) or see in Paul’s Online Notes: Improper Integrals (scroll down to “Discontinuous Integrand”) where there is more detail.

• Problem #6 specifically asked that you use a comparison test to determine whether or not the integral would converge. Some people just went ahead and tried to compute the integral. This was wrong (because it was not what was asked for) and a waste of time. Please read the instructions to the problems. For comparison tests, here are Paul’s Online Notes: Comparison Tests for Improper Integrals.

• In general, there were a number of test papers where many steps were missing and I am quite sure those steps could not be done in your heads.I do not know how this came to be, but please know that in the future I will have to make sure that people are not using extra sheets of paper and do not have their cell phones visible. I am very sorry to have to do this, for the majority who are honestly doing their best and following the instructions. Please read all the instructions on the cover sheet; you are responsible for following them. In particular, if I cannot see how you got your answer or any part of it, you may receive no credit: if in doubt, write it out!

It would not be a bad idea to look at both versions of the test solutions. Only two problems were actually different, and some were moved around.

If you did not receive full credit (a total of 40 points) for problems 5 and 6 on the third page, you have the opportunity to work similar problems to increase your score. In order for your score to increase, these must be done totally correctly and showing all work (except what you can easily do in your head: if in doubt, WRITE IT DOWN!)

These problems are due by the start of class on Wednesday 8 November.

MAT1575Test2-redoProblems