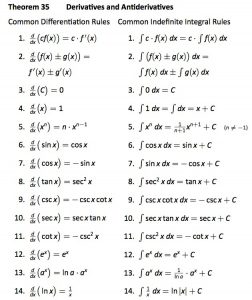I’ve started typing this up (as you can see, it’s got a lot of notes) but I’m getting error messages in some of the new things I’m trying to put in, so it’s incomplete. I’ll keep working on it, but wanted to give you these notes for now.
UPDATE: Here are the notes I have managed to get to work on this post. Some details remain for you to fill in! There is also a link to the Paul’s Notes page on L’Hôpital’s Rule which I highly recommend if you feel the urge to brush up on your skills! (Or even if you’ve totally forgotten what it is!)
Many of you have already started the WeBWorK, and I also extended the extra credit assignment: both are due Tuesday night!
There will be a quiz on partial fractions with either long division or irreducible quadratic factors (or both), plus one improper integral, next time.
Topics:
• Some homework problems from Partial Fractions 3
• Improper integrals (continued): the type where the interval of integration is infinite
Note: for working with improper integrals of this type, where we are taking limits as 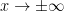 , it is very useful to keep in mind that any time we take a limit of a rational expression whose numerator is a constant and the denominator goes to infinity, that limit will be 0. So for example
, it is very useful to keep in mind that any time we take a limit of a rational expression whose numerator is a constant and the denominator goes to infinity, that limit will be 0. So for example
 for any
for any 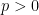

which means that 
and even
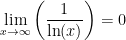
Also, we may have to use L’Hôpital’s Rule when we encounter the situation where the limit has one of the indefinite forms:
 ,
,  ,
,  , etc.
, etc.
Here are examples I discussed: (some details omitted, you should be able to fill in the missing steps though!)
![\displaystyle \int_{1}^{\infty}\frac{1}{x}\textrm{d}x = \lim_{b\rightarrow\infty}\left[\ln(x)\right]_{1}^{b} \displaystyle \int_{1}^{\infty}\frac{1}{x}\textrm{d}x = \lim_{b\rightarrow\infty}\left[\ln(x)\right]_{1}^{b}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7B1%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7Bx%7D%5Ctextrm%7Bd%7Dx+%3D+%5Clim_%7Bb%5Crightarrow%5Cinfty%7D%5Cleft%5B%5Cln%28x%29%5Cright%5D_%7B1%7D%5E%7Bb%7D+&bg=ffffff&fg=000000&s=0) diverges to infinity because
diverges to infinity because 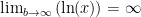
![\displaystyle \int_{-\infty}^{0}e^{x}\textrm{d}x = \lim_{a\rightarrow-\infty}\left[e^{x}\right]_{a}^{0} = 1 \displaystyle \int_{-\infty}^{0}e^{x}\textrm{d}x = \lim_{a\rightarrow-\infty}\left[e^{x}\right]_{a}^{0} = 1](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5Cint_%7B-%5Cinfty%7D%5E%7B0%7De%5E%7Bx%7D%5Ctextrm%7Bd%7Dx+%3D+%5Clim_%7Ba%5Crightarrow-%5Cinfty%7D%5Cleft%5Be%5E%7Bx%7D%5Cright%5D_%7Ba%7D%5E%7B0%7D+%3D+1&bg=ffffff&fg=000000&s=0) because
because 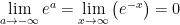
![\displaystyle\int_{-\infty}^{\infty}\frac{1}{1+x^{2}}\textrm{d}x=\lim_{a\rightarrow-\infty}\left[\tan^{-1}(x)\right]_{a}^{0}+\lim_{b\rightarrow \infty}\left[\tan^{-1}(x)\right]_{0}^{b} \displaystyle\int_{-\infty}^{\infty}\frac{1}{1+x^{2}}\textrm{d}x=\lim_{a\rightarrow-\infty}\left[\tan^{-1}(x)\right]_{a}^{0}+\lim_{b\rightarrow \infty}\left[\tan^{-1}(x)\right]_{0}^{b}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%5Cint_%7B-%5Cinfty%7D%5E%7B%5Cinfty%7D%5Cfrac%7B1%7D%7B1%2Bx%5E%7B2%7D%7D%5Ctextrm%7Bd%7Dx%3D%5Clim_%7Ba%5Crightarrow-%5Cinfty%7D%5Cleft%5B%5Ctan%5E%7B-1%7D%28x%29%5Cright%5D_%7Ba%7D%5E%7B0%7D%2B%5Clim_%7Bb%5Crightarrow+%5Cinfty%7D%5Cleft%5B%5Ctan%5E%7B-1%7D%28x%29%5Cright%5D_%7B0%7D%5E%7Bb%7D&bg=ffffff&fg=000000&s=0)

Comment: I find the limits for the inverse tangent by considering the graph of tangent in the period between  and
and 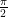 ; as
; as  in this part of the graph, the angle x is approaching
in this part of the graph, the angle x is approaching  , and as
, and as  in this part of the graph, the angle x is approaching
in this part of the graph, the angle x is approaching 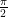 .
.
You can find the indefinite integral for 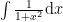 either by remembering that
either by remembering that 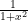 is the derivative of
is the derivative of 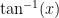 , or else by using a trig substitution
, or else by using a trig substitution 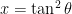 .
.
Example using L’Hôpital’s Rule:
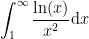
Note: this is Example 194 on p. 336 in the textbook, done there in considerable detail. We end up using L’Hôpital’s Rule to find 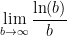 , which is an indefinite form of the type
, which is an indefinite form of the type  .
.
A general rule for integrals involving powers of x in the denominator: this will be useful for comparison to prove whether or not other indefinite integrals converge.
Consider the improper integral  with
with  .
.
What values of p will make it converge? When we integrate, we end up having to compute

This will go to 0 if the exponent is negative: otherwise, it will diverge to infinity.
So in order to have the integral converge, we need 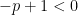 , which means that
, which means that 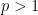 .
.
We already saw that this type of integral diverges when p =1, so now we know the following:
 converges when p>1, and it diverges when
converges when p>1, and it diverges when  .
.
Comparison Theorem:
Let f(x) and g(x) be functions such that both f(x) and g(x) are continuous on the interval 
and 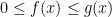 for all x in
for all x in 
Then:
• If  converges, then also
converges, then also  converges.
converges.
• If  diverges, then also
diverges, then also  diverges.
diverges.
Interpretation:
f(x) and g(x) have to be continuous on the given interval. Don’t forget to check this condition.
The condition 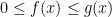 for all x in
for all x in  means that both f(x) and g(x) are non-negative functions on the interval, and the graph of f(x) is squeezed in between the x-axis and the graph of g(x).
means that both f(x) and g(x) are non-negative functions on the interval, and the graph of f(x) is squeezed in between the x-axis and the graph of g(x).
Now remember that the question of whether or not an improper integral of this type will converge, depends on how quickly the integrand goes to 0 as  .
.
The first part of this theorem,
• If  converges, then also
converges, then also  converges,
converges,
is saying that g(x) goes to 0 “fast enough” that its integral converges. Since the graph of f(x) is squeezed between the graph of g(x) and the x-axis, that means that f(x) goes to 0 at least as fast as g(x) does, maybe faster. So the integral of f(x) will also converge.
The second part of this theorem,
• If  diverges, then also
diverges, then also  diverges,
diverges,
is saying that f(x) does not go to 0 “fast enough” for its integral to converge. Since the graph of f(x) is squeezed between the graph of g(x) and the x-axis, that means that g(x) goes to 0 no faster than f(x) does, maybe slower. So the integral of g(x) will also diverge.
(A picture may help. See the graphs on p. 340 of the textbook.)
Example: see Ex. 197 part 2 on p. 340 (to the end of the page).
I also discussed the convergence of 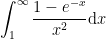 .
.
Since  for x in the interval
for x in the interval 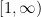 , the numerator
, the numerator  will always be a positive number less than 1 in that interval. So we can use comparison:
will always be a positive number less than 1 in that interval. So we can use comparison:
 on
on 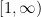
We know from before that  converges, so it follows that
converges, so it follows that 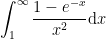 converges.
converges.
General comment on this comparison theorem: The theorem can only tell you that a certain integral converges: it does not tell you what the value of that integral is. In the example I just worked, we know that 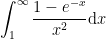 converges, but the most we can say about its value is that
converges, but the most we can say about its value is that  .
.
You may wonder why it is useful to know that something converges if we don’t know its actual value. One reason that it is useful to know this is that once we know that the integral converges, we can use numerical methods to estimate its value if all else fails. It is very dangerous to try to use numerical methods on an integral if we don’t know whether or not it converges!
Numerical methods are very important in applications (physics, etc) where many of the integrals we want to compute cannot be found explicitly even by the many methods you learn in this course!