Tag Archives: Line Graphs

Overview

What is Euler’s Method? Euler’s method is another way to solve differential equation problems in first order.  Most first order differential equations however fall into none of the categories such as linear, separable, or exact differential equation or differential equation.  How we solve first order differential equations is by knowing what we are looking for, if you are only looking for long term behavior of a solution you can always sketch a direction field.

What do we need?

Initial value y (a) = b

Differential equation   = f (t, y)

The slope at the initial point à f (a, b)

Initial point (a, b)

The many points to choose how many steps = h, (h+1)

Find the value of y at t = c, find y(c).

Summary of Euler’s Method

In order to use Euler’s Method to generate a numerical solution to an initial value problem of the form:

y′ = f(x, y)

y (x_o) = y_o

We decide upon what interval, starting at the initial condition, we desire to find the solution. We chop this interval into small subdivisions of length h. Then, using the initial condition as our starting point, we generate the rest of the solution by using the iterative formulas:

x_n+1 = x_n + h

y_n+1 = y_n + h f (x_n, y_n)

to find the coordinates of the points in our numerical solution. We terminate this process when we have reached the right end of the desired interval.

Video

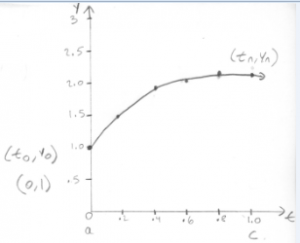
Sample Problem #1

Consider the initial value problem  = 3-2t-.5y, y (0) =1.  Find y (1)

Euler’s Method

Approximate y by generating a series of points,

(t0, y0) = (a, b) = initial condition

(t1, y1)

(t2, y2)…

(tn, yn) = (c, yn), where yn is an approximation of y(c)

Goal: Find yn

Step size = h = (c-a)/n

h = (1-0)/5 = .2

t0 = 0

t1 = 0+.2 = .2

t2 = .2+.2 = .4

t3 = .4+.2 = .6

t4 = .6+.2 = .8

t5 = .8+.2 = 1

To go from one point (ti, yi) to the next (ti+1, yi+1)

1. ti+1 = ti + h
2. find slope if (ti, yi) = k

Slope k

Slope = rise/run

k =   or d = k*h

yi +1 = yi +kh

yi +1 = yi + f (ti, yi)*h                                                                           = 3-2t-.5y

(t0, y0) = (0, 1)                                                                                    3-2(0)-.5= 2.5 =

(t1, y1) = (.2, 1.5)                                                                                yi+1 = 1+2.5(.2) = 1.5

(t2, y2) = (.4, 1.87)                                                                          yi+2 = yi+1 + f (ti, yi)*h

(t3, y3) = (.6, 2.123)                                                                        yi+3 = yi+2 + f (ti, yi)*h

(t4, y4) = (.8, 2.2707)                                                                      yi+4 = yi+3 + f (ti, yi)*h

(t5, y5) = (1, 2.32363)                                                                     yi+5 = yi+4 + f (ti, yi)*h

Chart

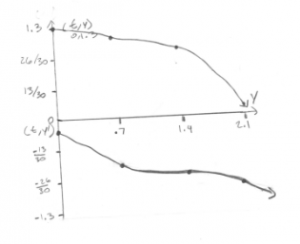
Sample Problem #2

Given the initial value problem y’ = sin (t +y +2), y (0) = 1.4, find approximate values of the solution at t = .7, t = 1.4 and t = 2.1, using Euler’s method with h = .7.

t = .7, t = 1.4, t = 2.1   h=.7

y1 = y0 + h(y’0)

y1’ = sin (t+y+2)

y0’ = sin (0+1.3+2+2) = sin (3.3)

y1 = 1.3 + (.7)*(-.157746)

y1’ = sin (.7+1.89578+2)

y1’ = -.680163

y2 = 1.189578 + (.7) (-.680163)

y2’ = sin (1.4+.713464+2)

y2’ = -.825942

y3 = .713464 + (.7) (-.825942)

y3’ = sin (2.1+2+.135305)

y3’ = -.8883375

t	y	y’
0	1.3	-.157746
.7	1.189578	-.680163
1.4	.713464	-.825942
2.1	.135305	-.8883375

Chart