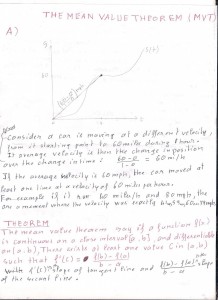
You Cut. I Choose. I have an older brother in Texas. As kids, we adhered to a strict rule when it came to sharing. Whatever the commodity, one of us cut it in two, and the other got to choose either portion. The system worked better and better as we grew up; each of us developed faith in the other’s sense of spatial analysis. When either of us had to do the cutting, we would divide the parts as evenly as possible.
It makes immediate sense that we can cut an object in half, provided that we know where to cut. But how can we prove it?
Intermediate Value Theorem. From Single Variable Calculus Early Transcendentals by Jon Rogawski: The Intermediate Value Theorem says that if a function f(x) is continuous on a closed interval [a,b] and f(a) doesn’t equal f(b), then for every value M between f(a) and f(b), there exists at least one value c on the interval (a,b) such that f(c)=M.
Informally, this means that if you can give a slice of pie to Andrew, or you can give the same slice to Joe, then you can give half a slice to each, and disappoint them both.
How to cut a piece of ham. Consider a 2-dimensional slice of ham.
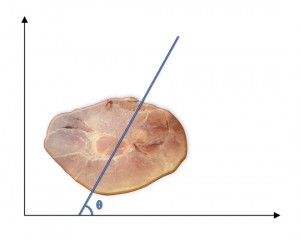
Let’s prove that for any angle θ, it is possible to cut the slice of ham in half with a cut of incline θ.
First we’ll restrict θ to (0,pi/2).
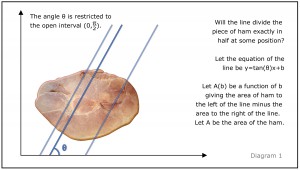
Let the equation of the line be y=tan(θ)x+b.
Let A(b) be a function of b giving the area of ham to the left of the line minus the area to the right of the line.
Let A be the area of the ham.
If the whole slice is to the right of the line y=(tanθ)x+b, A(b)=-A.
If the whole slice is to the left of the line y=(tanθ)x+b, A(b) =A.
Consider a box bounding the ham on the left, right, top, and bottom.
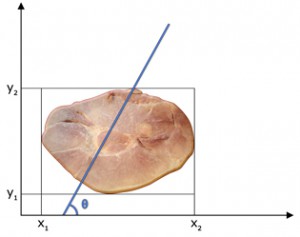
If b=-tan(θ)x1+y2 then the line y=tan(θ)x+b will pass through the point (x1,y2), and A(b)=-A.
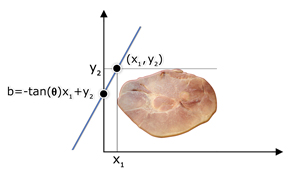
If b=-tan(θ)x2+y1 then the line y=tan(θ)x+b will pass through the point (x2,y1), and A(b)=A.
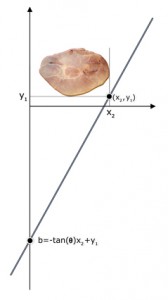
If we apply the Intermediate value theorem, there must exist a value c such that A(c)=0, assuming that the function is continuous. A line with angle θ and y intersect c, y=tan(θ)x+c, cuts the ham in half.
A similar argument holds for each of the other three quadrants (we originally restrict θ to (0,pi/2).
See Single Variable Calculus Early Transcendentals by Jon Rogawski: page 110 for an exercise relating to exceptions when θ=0, pi/2, pi, and 3pi/2.
Whipped Cream, or a Slice of Bread. Things aren’t this simple in real life. Divide a pie, and you might end up arguing over who gets more whipped cream. What about two objects? Can we divide them both in half? With a single slice?
Joking apart, it seems like a single line should be able to cut two objects in half, as long as the angle and position of the line are suitable. But how do we use the Intermediate Value Theorem to prove it?
Consider the slice of ham from before, but add a slice of bread. Plop it down wherever.

Allow θ to be any angle between 0 and pi. We have just shown that there must be a line with slope tan(θ) that cuts the ham in half. This is true for all values of θ between 0 and 2pi.
If for every angle (θ) and value b such that tan(θ)x+b cuts the ham in half the bread is also cut in half, then any slice that cuts one of them equally cuts both equally.
But if we can find a θ and b such that the ham is cut in half and the bread is not cut in half, we can use the Intermediate Value Theorem again. If any ham-bisecting slice cuts the bread unequally, consider the same slice rotated pi radians so that the area of bread on either side of the slice is reversed.
Applying our area function A(b) to the bread, we go from a negative value to a positive value (or vice versa) when we rotate θ by pi radians. Using the Intermediate Value Theorem as before, we can show that for some θ and b, A(b)=0, and the line bisecting the ham also bisects the slice of bread.
But what about a real ham sandwich?
With a Cherry on Top. It turns out that all of this can be generalized: Given n measurable “objects” in n-dimensional space, it is possible to divide all of them in half (with respect to their measure, i.e. volume) with a single (n − 1)-dimensional hyperplane. (Wikipedia: ‘ham sandwich theorem.’)
In 3 dimensions, we can cut two pieces of bread and some ham in two with a plane:
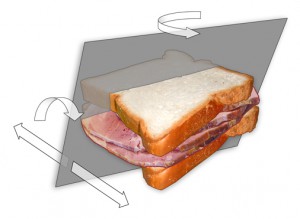
All this math is making me hungry.