The assignment below is due BEFORE CLASS on Thursday, October 5th (it is essential that you complete it before class, as we will be doing a class activity building on the assignment).
We are going to play a game creating walking tours of cities with bridges. We begin in the city of King’s Mountain, which is built on four land masses – both shores of a river and two islands in midstream – connected by a total of seven bridges (shown in green).

EXAMPLE 1: Can you create a walking tour of the city that crosses every bridge exactly once? You can begin anywhere you like, and end anywhere you like, as long as you cross each bridge just once.
Background – Graph Theory
We can simplify the picture of King’s Mountain to make it easier to deal with:
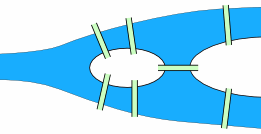
The key elements of the map are the four land masses (let’s label them A, B, C, and D) and the seven bridges (p,q,r,s,t,u and v) (thanks to mathisfun.com for the images):
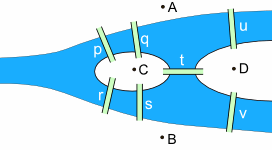
For the purposes of our problem, we can simply think about each land mass as a point (A, B, C, and D), and the bridges as lines connecting the points (p,q,r,s,t,u and v) – like this:
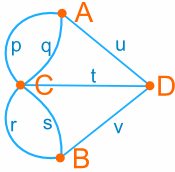
We call this kind of picture a graph – the points are called vertices and the the lines are called edges. Our goal of finding “a walking tour that crosses each bridge once” is now matter of tracing out all the edges without lifting our pencil (and without repeating any edge).
Assignment, Due Thursday 10/5 (beginning of class)
Warm up (This Warm Up is just for practice – you do NOT need to submit your answers – see below for the three-part Assignment to be submitted). The following examples build on EXAMPLE 1 above.
WARM-UP EXAMPLE 2: If you are given the freedom to build one new bridge in King’s Mountain (“make one new edge in the graph”), can you do it in such a way the walking tour becomes possible? Do it!
WARM-UP EXAMPLE 3: If you are given the freedom to destroy one bridge (“erase one edge”), can you do it in such a way that the walking tour becomes possible? Do it!
WARM-UP EXAMPLE 4: Construct walking tours for each of the following graphs (or decide if it is impossible).
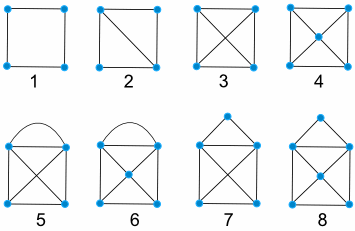
Assignment. Your assignment has 4 parts.
PART 1. Leave a comment responding to EXAMPLE 4 (above), telling us for each one of the 8 graphs whether a walking tour is possible or not. You only have to state whether it is possible or impossible for each one.
PART 2. Challenge your friends: Now it’s up to you to build your own graph, and challenge your classmates to construct a walking tour (or to determine if it is impossible). It can consist of as many points as you wish, and as many bridges (edges) connecting them. You MUST label your points “A, B, C…” etc. When you’re finished, decide for yourself if a walking tour crossing each bridge exactly once is possible. Remember, the most challenging puzzles are the ones where the answer is difficult to determine. Post two puzzles in the comments. See the note “POSTING YOUR PUZZLE ONLINE” below for instructions on how to draw and share graphs online.
PART 3. Solve a friend’s puzzle. Leave a response to a friend’s posted puzzle, giving a solution. TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER.
Example:
Here is a puzzle: http://sketchtoy.com/67467551
Here is a solution: (start at A) – A, B, D, A, E, B, C, E
PART 4. The third part of your assignment is to write a short paragraph (at least 3 sentences) responding to the following prompt. Be sure to respond to each part:
Writing Prompt: Did you enjoy this assignment? Why or why not? Describe a connection between this assignment and our work in the class. (If you don’t believe there is a connection, try to imagine why we are doing this). Leave your response in the comments.
POSTING YOUR PUZZLE ONLINE. I recommend the site sketchtoy.com – it allows you to draw something, then click “SAVE” and get a link to your drawing. You can post the link in a comment, and we’ll be able to click on it and view your drawing. Don’t worry if it’s not pretty! For example, here is a graph that I drew (can you find a walking tour that crosses all edges?): http://sketchtoy.com/67467556




Part 1
1. Possible
2. Possible
3. Possible
4. Impossible
5. Possible
6. Impossible
7. Impossible
8. Possible
Part 2
Puzzle 1 http://sketchtoy.com/68337721
Puzzle 2 http://sketchtoy.com/68337730
Part 4. I enjoyed being able to challenge myself to find a way to cross the bridges because it made me have to view the problem from different perspectives. I am not sure of the connection to the stuff that we are doing in class with lists, sets, and statements. There might be a slight connection between having choices like when we make lists and have to choose from a larger set. That is my best guess thus far.
Possible solution to Zaniyasa
a)starting @ ‘a’, a>b (traveling from ‘a’ to ‘b’), b>g, g>e, e>d, d>c, c>g, g>f, f>a
b)starting @ ‘a’, a
Possible solution to Zaniyasa
Puzzle one-starting @ ‘a’, a>b (traveling from ‘a’ to ‘b’), b>g, g>e, e>d, d>c, c>g, g>f, f>a
Puzzle two-starting @ ‘a’, a>b,b>I, I>j, j>k, k>h, h>g, g>f, f>a, a>c, c>d, d>e, e>k
Hi Zaniyasa, see my solution for your puzzle below, I liked so much the way you draw your puzzle.
1. A-B-G-E-D-C-F-A
2.A-B-I-J-K-H-G-F-A-B-C-D-E-K
Thanks for starting off, Zaniya – I think your puzzles are great, I especially like that the second one almost looks like a drawing of something (a ship maybe?).
Sketch 1 – A-B-G-E-D-C-F-A
Sketch 2 – A-B-I-J-K-H-G-F-A-C-D-E-K
1) 1) possible 2) possible 3) not possible 4) not possible 5) possible 6) possible 7) possible 8) possible
2) http://sketchtoy.com/68343186
3) solution to Zaniyasa
a)starting @ ‘a’, a>b (traveling from ‘a’ to ‘b’), b>g, g>e, e>d, d>c, c>g, g>f, f>a
b)starting @ ‘a’, a>b, b>I, I>j, j>k, k>h, h>g, g>f, f>a, a>c, c> d, d>e, e>k
4) Working with puzzles is fun and challenging. Creating puzzles is even more challenging. We are working with sets and subsets in these examples. We have groping of points, land masses, connected by subsets, bridges.
Solutions:
Puzzle 1: BCEDBFEAB
Puzzle 2: DCBAEFBDEC
Solution to Kelly’s puzzles:
Puzzle 1: (Start at E)- E, D, B, C, E, A, B, F, E
Puzzle 2: (Start at D)- D, E, F, B, A, E, C, B, D, C
I like the symmetry and patterns you used – and the fact that your two puzzles are quite similar. Sometimes a small change can make a big difference!
PART 1.
graph # 1 – possible graph# 5 – possible
graph# 2 – possible graph# 6 – possible
graph#3 – impossible graph# 7 – possible
graph#4 – impossible graph #8 – possible
Part 2.
See the link below for my graph:
http://sketchtoy.com/68343239
http://sketchtoy.com/68343266
Part 4.
This activity really made my brain muscles worked best as they can! I literally spent one hour to just finish the warm-up examples. I change my answers a few times. For example, I thought that #5, and #7 have no solution, but after I tried many different ways to cross the points. I found out one solution for #5. Then I thought if #5 has a solution then #7 must has a solution too. And finally I was able to solve #7 with the same technique I used for #5. I enjoy the process of solving these puzzles, it a very interesting thing to do. Whit what we leaned so far, I personally think that this actively show that when we try to solve a problem. if one way is not working, we should try other ways to solve it. If still can’t find a solution, then it may has no solution at all. In another word, the gaol of this activity is teach us a processes of thinking or reasoning.
Problem solving is definitely important in this assignment – both for solving and for creating puzzles. I like your first puzzle a lot – it’s almost a “puzzle inside of a puzzle”.
Part 1:
1. possible
2. possible
3. not possible
4. not possible
5. possible
6. possible
7. possible
8. possible
Part 2:
http://sketchtoy.com/68343918
http://sketchtoy.com/68343923
Part 4:
I really enjoyed this assignment. I’m a big puzzle fan. I’m not really sure what the connection might be between this assignment and the work we are doing. From what I got from this assignment, there are many ways to designing a puzzle as well as solving it. Maybe this is similar when we are creating a list.
puzzle 1: start at A, ABCEFHIGFD
puzzle 2: A,B,E,D,A,B,C
Great drawing strategy – you didn’t give anything away by the way you sketch the puzzles.
Part 1-
1. Possible
2. Possible
3. Impossible
4. Impossible
5. Possible
6. Possible
7. Possible
8. Possible
Part 2-
-Puzzle 1: http://sketchtoy.com/68344573
-Puzzle 2: http://sketchtoy.com/68344057
Part 3-
Solution to Kelly.
Puzzle 1: (Start at E)- E, D, B, C, E, A, B, F, E
Puzzle 2: (Start at D)- D, E, F, B, A, E, C, B, D, C
Part 4-
I enjoyed this assignment because it was both interesting and challenging to solve this puzzle. I love working on puzzle since you create patterns in your mind to figure out solutions to trying to solve it. A connection between this assignment and our work in the class is that it might have to deal with logic. Since we take our time to figure out the next thing we have to do to solve this puzzle for example. Another thing, since were learning about non-repetitive, like the puzzle where cannot go over the line twice is just like the non-repetitive list we been doing in class.
Hi Stephanie,
See my answer below to your puzzle:
1. H-F-G-C-H-G-B-F-A-E-D-H-E-F
2. A-C-B-A-I-F-E-D-C-F-G-H-I-C-E-G-I-B
Puzzle #1
ABCDEFGHIACEGIFCIB
Puzzle #2
HCGBFAEDHEHGFH
FEDHCGBFAEHFGH
I love how you puzzle has so many pathways and still has a solution
Great symmetric shapes & patterns, Stephanie! And I like the connection to non-repetitive lists – this might prove useful.
Part 1:
1 Possible
2 Possible
3 Impossible
4 Impossible
5 Possible
6 Possible
7 Possible
8 Possible
Part 2:
Puzzle 1: http://sketchtoy.com/68345525
Puzzle 2: http://sketchtoy.com/68345533
Part 3:
Solution to Zaniyasa:
Puzzle 1: (Start at A) – A,B,G,E,D,C,F,A
Puzzle 2: (Start at A) – A,B,I,J,K,H,G,F,A,B,C,D,E,K
Solution to Kelly.
Puzzle 1: (Start at E)- E, C, B, A, E, D, B, F, E
Puzzle 2: (Start at C)- C, E, A, B, C, D, B, F, E, D
Part 4:
I enjoyed this assignment because I like puzzles and I like to challenge my brain to make it works better. I think this assignment is related to creating or proving non-repetitive lists because we are only allowed to cross each bridge just once.
Your first puzzle looks to me almost like a three dimensional shape (a cube?) – cool!
Part I
1. Possible
2. Possible
3. Possible
4. Impossible
5. Possible
6. Impossible
7. Possible
8. Impossible
Part II
My puzzles are:
hhtp://sketchtoy.com68346628
hhtp://sketchtoy.com68346643
Part III
Hi Zaniyasa
Here is my answer for your number 2
ABGEDCGFA
Part IV
I really enjoy the puzzles I could have spend more time to practice. Puzzle is something that makes the brain work in a way that we do not even aware or even imagine how we can go deeper in thinking. In really this drawing puzzle also relates to the factorials list that the professor has been working on since last. week.
Solutions
Puzzle 1
ABCDEFGHIJA
Puzzle 2
AecDBeFcBA
I’m curious how it relates to factorials. Hmm.. I guess you can multiply the number of choices you have to figure out how many possibilities there are.
I wonder if a puzzle can be designed with exactly x! factorial number of possibilities which is evident from the design
I love puzzles too! The connection between gut feeling and conscious thought is a hallmark of good math.
Part 1:
1. Possible
2. Possible
3. Impossible
4. Impossible
5. Possible
6. Impossible
7. Possible
8. Impossible
Part 2:
puzzle 1: http://sketchtoy.com/68346689 Impossible
puzzle 2: http://sketchtoy.com/68346699 Possible
(sorry for putting so many letters got carried away lol)
Part 3: I Loved this activity. I sat with my husband and we sketched so many possible puzzles and also try to solve the puzzles given. I think this relates to the class because many times we think there is only one way to prove a math problem but just like a puzzle where you can make a tour a, b, c, d and the same tour b,c,d,a. This is what will happen many times. In some cases, like the puzzles, there is just one way to prove the problems but other times there is endless ways to start the problem to get the same answer.
I also think it’s quite interesting to consider how many ways there are to solve these – some have many solutions, and some few (and of course, some have none). Definitely worthy of further consideration….
ps. I love that you did these with your husband
First label the vertexes 1-4 for the square starting from the bottom left and going counter clock wise for all problems. Then we label the additional vertex if any as 5. For question number 8 we label the center vertex as 6.
If we consider 2 problems equivalent if an answer could be constructed following the same path (while ignoring scale and curvature). Then the equivalences and the solutions from vertex to vertex would be the following:
1 and 2 are not equivalent and have solutions.
1. 12341
2. 412432
3 and 4 are are equivalent and have No Solution 1 Extra Step is Required to get the following
3. 123413 (Extra step is here) 24
4. 1234153(Extra step is here in same location)254
5, 6, 7 and 8 are equivalent and have solutions
5. 12341342
6. 1234153452
7. 123413542
8. 12341635462
Part 2
Question 1
http://sketchtoy.com/68346988
Which bridges can be added/removed to give this a solution.
Which ones cant be removed?
Hint: Adding/Removing only 1 bridge will not give you an answer.
Question 2
http://sketchtoy.com/68346981
It wasn’t stated anywhere that the lines had to be connected so I made one that isn’t – Has no Solution
What is the minimum number of vertexes that must be visited to traverse all lines?
What is the minimum number of line additions/removals that allow a solution?
Part 4
I loved doing this exercise. Since it forced me to think about the problem in different ways, especially since I learned how mathmations come up with derivations. I initially started with a decision tree to come up with all possibility and run through them 1 by 1 while eliminating the symmetric possibilities. I then noticed some patterns which i used to create a set of definitions and rules that prove when it is impossible to find a solution. (whether its right or wrong or incomplete I was able to think deeply about the intrinsic nature of the objects being dealt with and I am highly thankful for this opportunity).
This topic relates to combinatorics that we are covering since each choice we make such as what vertex to start from. leads to several second choices each of which leads to several third choices. So we can count all the possible routes that can be taken before a solution is found. and how many routes exist. Are the Routes all symmetrically equivalent and so on.
I really like the questions you ask in #2 – these are great!
Part 1
1) Possible
2) Possible
3) Impossible
4) Impossible
5) Possible
6) Possible
7) Possible
8) Possible
http://sketchtoy.com/68347208
http://sketchtoy.com/68347214
I enjoyed this assignment because I enjoy doing puzzles like this. The more challenging the puzzle the more I enjoy it. My favorite kind of puzzles are the ones that require logically thinking and trying to figure out how to best solve a puzzle, or if solving a puzzle is even possible. Our class deals with logic, so we it directly relates to the material that we discuss because solving these puzzles requires use of logic.