The assignment below is due BEFORE CLASS on Thursday, October 5th (it is essential that you complete it before class, as we will be doing a class activity building on the assignment).
We are going to play a game creating walking tours of cities with bridges. We begin in the city of King’s Mountain, which is built on four land masses – both shores of a river and two islands in midstream – connected by a total of seven bridges (shown in green).

EXAMPLE 1: Can you create a walking tour of the city that crosses every bridge exactly once? You can begin anywhere you like, and end anywhere you like, as long as you cross each bridge just once.
Background – Graph Theory
We can simplify the picture of King’s Mountain to make it easier to deal with:
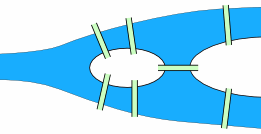
The key elements of the map are the four land masses (let’s label them A, B, C, and D) and the seven bridges (p,q,r,s,t,u and v) (thanks to mathisfun.com for the images):
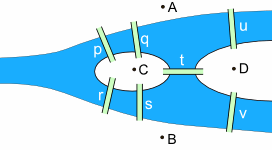
For the purposes of our problem, we can simply think about each land mass as a point (A, B, C, and D), and the bridges as lines connecting the points (p,q,r,s,t,u and v) – like this:
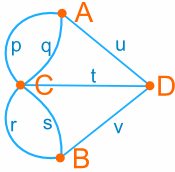
We call this kind of picture a graph – the points are called vertices and the the lines are called edges. Our goal of finding “a walking tour that crosses each bridge once” is now matter of tracing out all the edges without lifting our pencil (and without repeating any edge).
Assignment, Due Thursday 10/5 (beginning of class)
Warm up (This Warm Up is just for practice – you do NOT need to submit your answers – see below for the three-part Assignment to be submitted). The following examples build on EXAMPLE 1 above.
WARM-UP EXAMPLE 2: If you are given the freedom to build one new bridge in King’s Mountain (“make one new edge in the graph”), can you do it in such a way the walking tour becomes possible? Do it!
WARM-UP EXAMPLE 3: If you are given the freedom to destroy one bridge (“erase one edge”), can you do it in such a way that the walking tour becomes possible? Do it!
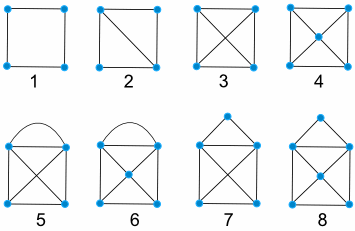
WARM-UP EXAMPLE 4: Construct walking tours for each of the following graphs (or decide if it is impossible).
Assignment. Your assignment has 4 parts.
PART 1. Leave a comment responding to EXAMPLE 4 (above), telling us for each one of the 8 graphs whether a walking tour is possible or not. You only have to state whether it is possible or impossible for each one.
PART 2. Challenge your friends: Now it’s up to you to build your own graph, and challenge your classmates to construct a walking tour (or to determine if it is impossible). It can consist of as many points as you wish, and as many bridges (edges) connecting them. You MUST label your points “A, B, C…” etc. When you’re finished, decide for yourself if a walking tour crossing each bridge exactly once is possible. Remember, the most challenging puzzles are the ones where the answer is difficult to determine. Post two puzzles in the comments. See the note “POSTING YOUR PUZZLE ONLINE” below for instructions on how to draw and share graphs online.
PART 3. Solve a friend’s puzzle. Leave a response to a friend’s posted puzzle, giving a solution. TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER.
Example:
Here is a puzzle: http://sketchtoy.com/67467551
Here is a solution: (start at A) – A, B, D, A, E, B, C, E
PART 4. The third part of your assignment is to write a short paragraph (at least 3 sentences) responding to the following prompt. Be sure to respond to each part:
Writing Prompt: Did you enjoy this assignment? Why or why not? Describe a connection between this assignment and our work in the class. (If you don’t believe there is a connection, try to imagine why we are doing this). Leave your response in the comments.
POSTING YOUR PUZZLE ONLINE. I recommend the site sketchtoy.com – it allows you to draw something, then click “SAVE” and get a link to your drawing. You can post the link in a comment, and we’ll be able to click on it and view your drawing. Don’t worry if it’s not pretty! For example, here is a graph that I drew (can you find a walking tour that crosses all edges?): http://sketchtoy.com/67467556




Recent Comments