It seems I’ve mostly recovered from whatever was making me feel bad this morning. Thanks for your well-wishes and sorry you had to wake up early today for nothing! I hope you’re all working hard on your take-home tests and thinking about group project topics. One of your WebWork sets due next Tuesday includes material that would have been covered during today’s class. Below, I’ll give you a few short readings/exercises to do before Monday’s class so that today’s missed class doesn’t put us too far behind schedule. It shouldn’t take you more than 15 minutes to go through the whole thing
3.5 Higher derivatives
Some of you have been anticipating this for a while: since the derivative  of a function
of a function  is itself a function, you can take the derivative of the derivative. We call the derivative of the derivative of
is itself a function, you can take the derivative of the derivative. We call the derivative of the derivative of  the second derivative of
the second derivative of  and denote it by
and denote it by 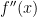 . Similarly, the third derivative of
. Similarly, the third derivative of  , is the derivative of the derivative of the derivative of
, is the derivative of the derivative of the derivative of  . The third derivative is denoted by
. The third derivative is denoted by 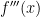 or sometimes
or sometimes  . The nth derivative is usually denoted
. The nth derivative is usually denoted  . Here, you can imagine n is any positive integer, but you can include n=0 if you define the zeroth derivative of
. Here, you can imagine n is any positive integer, but you can include n=0 if you define the zeroth derivative of  as
as  itself.
itself.
Exercise: Let  . Find all the derivatives of
. Find all the derivatives of  .
.
An application: Remember that getting-caught-speeding example from the first week of class. In groups you turned a story about driving into a position-versus-time graph. The first part of the story said something like, “You pulled out of the driveway slowly and then sped up.” Every group’s graph started off increasing slowly and then curved up and increased more quickly. First, remember that the derivative of a position function is an instantaneous velocity function. Since the graph for this portion is increasing, the velocity is positive…you’re driving away from your house so the distance between you and the house is increasing. Second, the derivative of a velocity function is the instantaneous rate of change of velocity…also known as acceleration. Since you were speeding up, the acceleration is positive…so the position graph is curving up. (We say this part of the graph is concave up. If you were slowing down, but still moving forward, the velocity would be positive and the graph of the position function increasing, but the acceleration would be negative so the graph of the position function would be concave down.)
Another similar example is an object dropped from rest. The distance the object falls in t seconds is  meters. Its instantaneous velocity is
meters. Its instantaneous velocity is  and its instantaneous acceleration is
and its instantaneous acceleration is 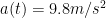 . If you’ve ever taken a physics course, you might recognize this as the constant acceleration due to gravity, sometimes denoted by g.
. If you’ve ever taken a physics course, you might recognize this as the constant acceleration due to gravity, sometimes denoted by g.
4.1 Linearization
Shifting gears a little, remember that the tangent line to a curve at a point is the line that best approximates the curve at that point. As long as the curve is smooth, there is a tangent line and we say that the curve is locally linear. Linear functions are among the easiest functions to do calculations with, so (if you can tolerate a little error) you might use the tangent line to the graph of a function rather than the function itself. This will only work if the only points you’re interested in are close enough to the point of tangency.
Exercise: Head on over to Desmos or pull out your graphing calculator.
- Graph the function
 .
.
- We’ll focus on the point
 . Zoom in as much as you can; notice that the graph is approximately a line.
. Zoom in as much as you can; notice that the graph is approximately a line.
- By hand, find the equation of the tangent line to the graph of
 at
at  .
.
- Graph the tangent line and zoom in on
 ; notice that the graph of the function and the tangent line are approximately the same thing. Zoom out and notice that the graphs are far apart for points far away from
; notice that the graph of the function and the tangent line are approximately the same thing. Zoom out and notice that the graphs are far apart for points far away from  .
.
- Use your calculator to find the y-coordinate of the point on the graph of
 with x-coordinate 4.1. (the calculator will spit out a decimal approximation; that’s okay, just record as many decimal places as you can tolerate.)
with x-coordinate 4.1. (the calculator will spit out a decimal approximation; that’s okay, just record as many decimal places as you can tolerate.)
- By hand, find the y-coordinate of the point on the tangent line with x-coordinate 4.1. (You’ll probably have to remember how to perform long division of numbers when there’s a decimal.)
- Compare your answers for 5 and 6 by subtracting one from the other. If everything went as planned, the difference should be small. This is what is meant by the error.
The point of this exercise is that you were able to approximate 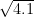 by hand, because 4.1 is close to 4, whose square root is easy.
by hand, because 4.1 is close to 4, whose square root is easy.
There’s nothing special about the square root function…you can approximate values for other functions too. The linearization of a function  at a point
at a point  is
is 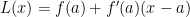 . Notice that the graph of the linearization is just the tangent line to
. Notice that the graph of the linearization is just the tangent line to  at the point
at the point  .
.
Exercise: Use the same steps above to approximate 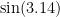 . (Notice that 3.14 is close to, but not equal to
. (Notice that 3.14 is close to, but not equal to 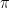 .) Calculate the error.
.) Calculate the error.
, the function that models the volume of water that’s flowed in at time
, and
, the function that models the amount of water that’s flowed out at time
. My version of the question says that water is flowing out at 10,000 cubic cm per minute, so that means
. Since it says that water is flowing in at a constant rate, I’m going to let
; then my job is to find
.
be the volume of the water that’s actually in the tank at time
, then
, (this assumes that at time
there is no water in the tank, but this assumption won’t end up mattering) so
.