Solve the following question by using chain rule.
y=((x-3)/(x+3))^4
-
Recent Posts
Recent Comments
- Maloney on Ham Sandwich Theorem
- Jimmy Choy on Ham Sandwich Theorem
- mouhamath ciss on Mean value theorem- M. CISS
- Kate Poirier on Office hour today
- NaiBing on Extra credit
Archives
Categories
Meta
y’=4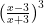
( 
I think you also have the right answer, and I see that you did use the chain rule, though it isn’t apparent at first since you didn’t actually put either g’ in (1 in both of your applications of the chain rule.)
I think you’ve got the answer. The part that didn’t parse is 6/(x+3)^2, right?
Well, it didn’t complete it through the end, I just applied the formula and I got that big equation. I’m not sure if we really have to solve it through the end on the test(which is all algebra).
a derivative is a derivative… if the question just ask u to find the derivative, u can basically give it in any form even if its not simplified as long as the answers are right and equal
Hey guys, I haven’t checked any of your answers, but I’m assuming you’re on the right track! If any portion of LaTeX doesn’t parse, you can always mouseover the “Formula does not parse” text to see what code didn’t compile.
Abu, your question is a nice straighforward one, but I have one comment about the wording. “Solve the following question…” doesn’t really ask what I think you mean to ask. Since you’ve included “..using the chain rule” I have to assume that what you mean is “Differentiate the function,” or just “Differentiate,” or “Find the derivative.”