Announcements
WebWork schedule:
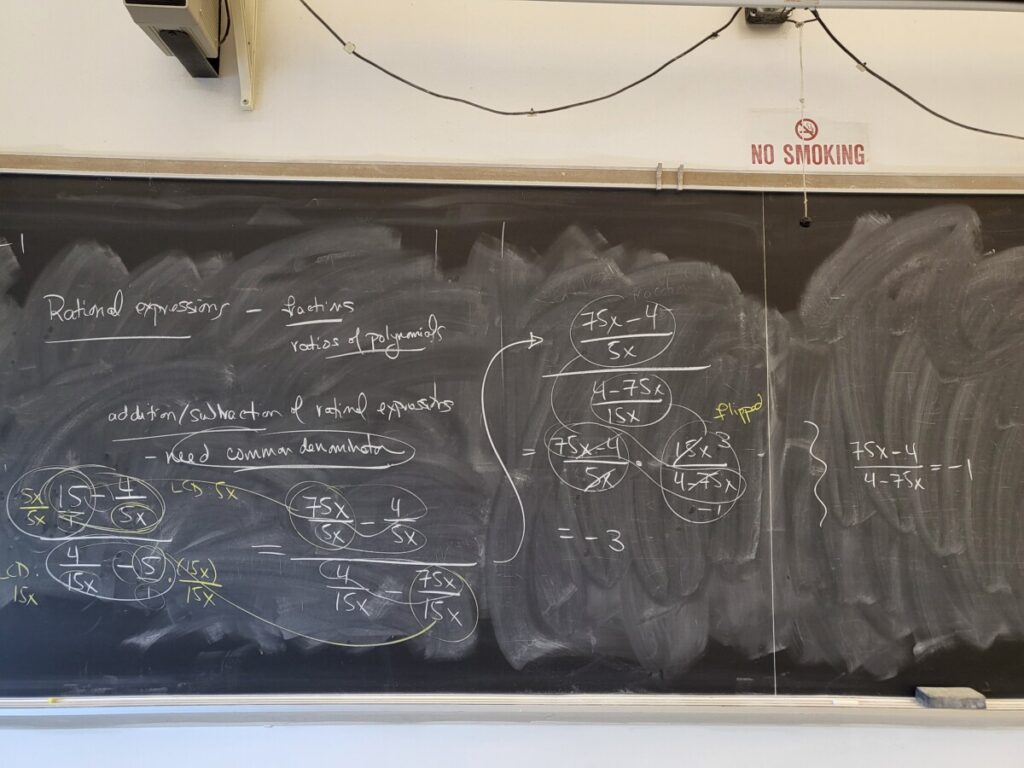
- Rational Expressions-Complex Fractions 2 – due Fri March 22 (Sec 1.3.4)
- Radical Expressions-Adding and Subtracting – due Fri March 22 (Sec 1.4.4)
- Radical Expressions-Multiplying – due Mon March 25 (Sec 1.4.4)
Topics
We continued studying “radical expressions”–we briefly discussed “higher roots” (such as cube roots, fourth roots, etc.) and now these can be expressed as “rational exponents”:

We then revisited factoring a quadratic polynomial, and how we can use a factorization to solve a quadratic equation. We can also solve such a quadratic equation using the quadratic formula (which involves a square root):
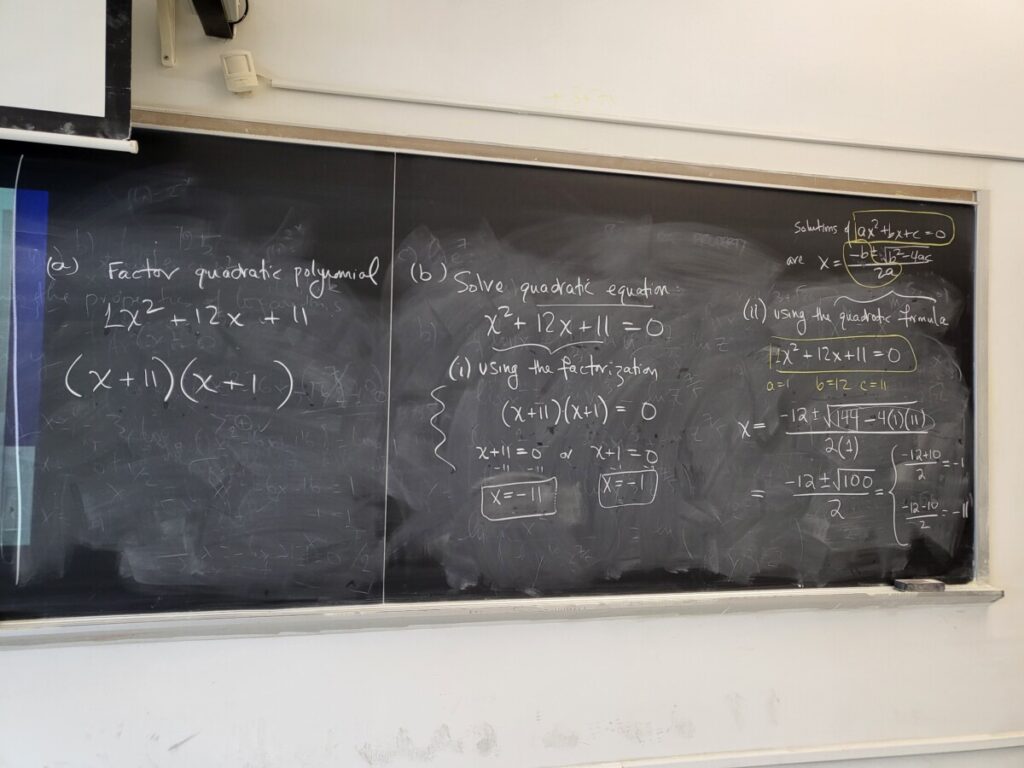
But for a quadratic polynomial that doesn’t factor, we need to use the quadratic formula–and then we usually can simplify the square root involved, using the techniques we have been studying:

We also looked at the graphs of these quadratic polynomials in Desmos, and noticed how the solutions of the quadratic equation correspond to the x-intercepts of the graph.
We finished by going through some more WebWork exercises on adding/subtracting and then multiplying square roots:

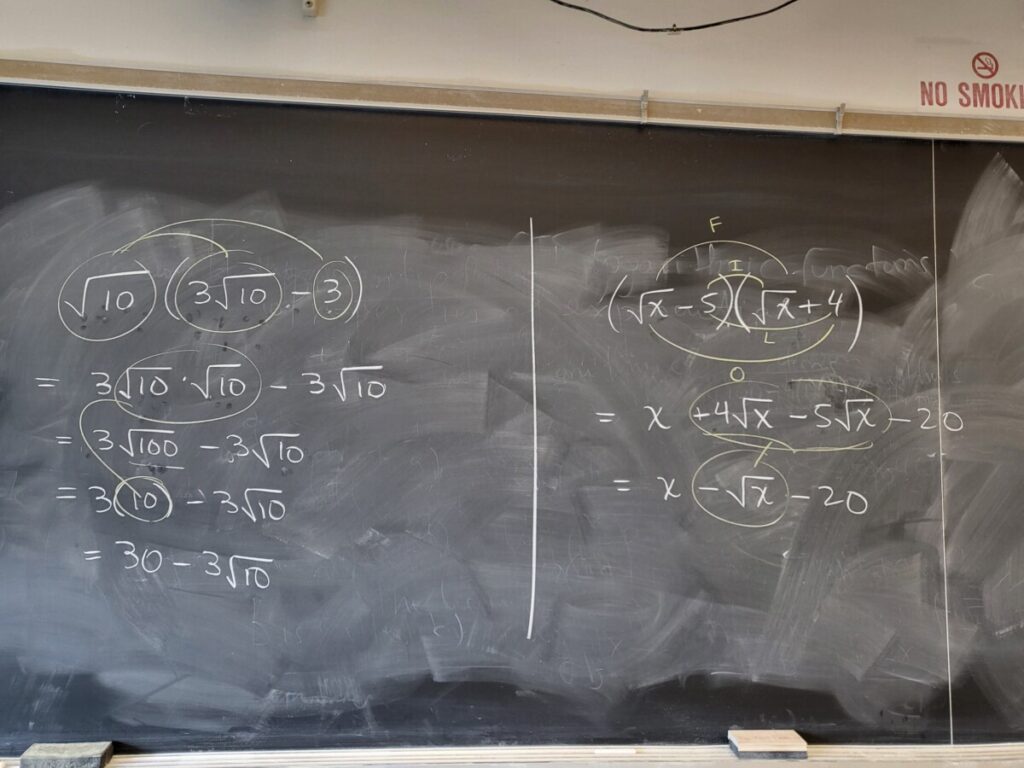
Note that exercises above involve the distributive property and FOIL.


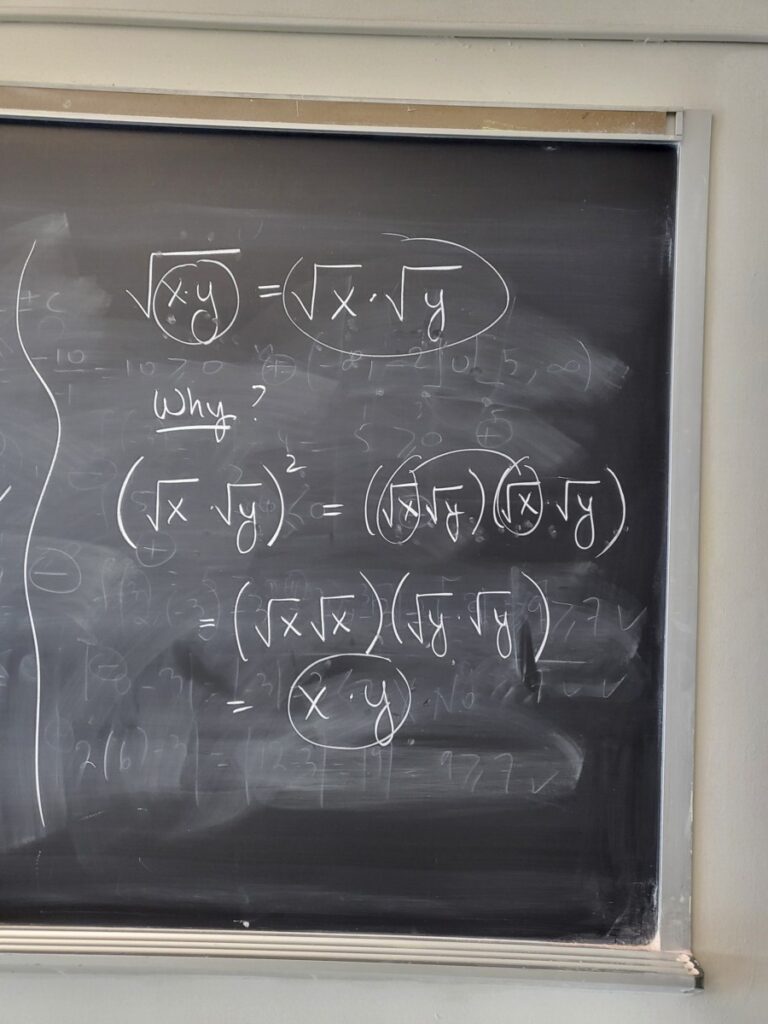


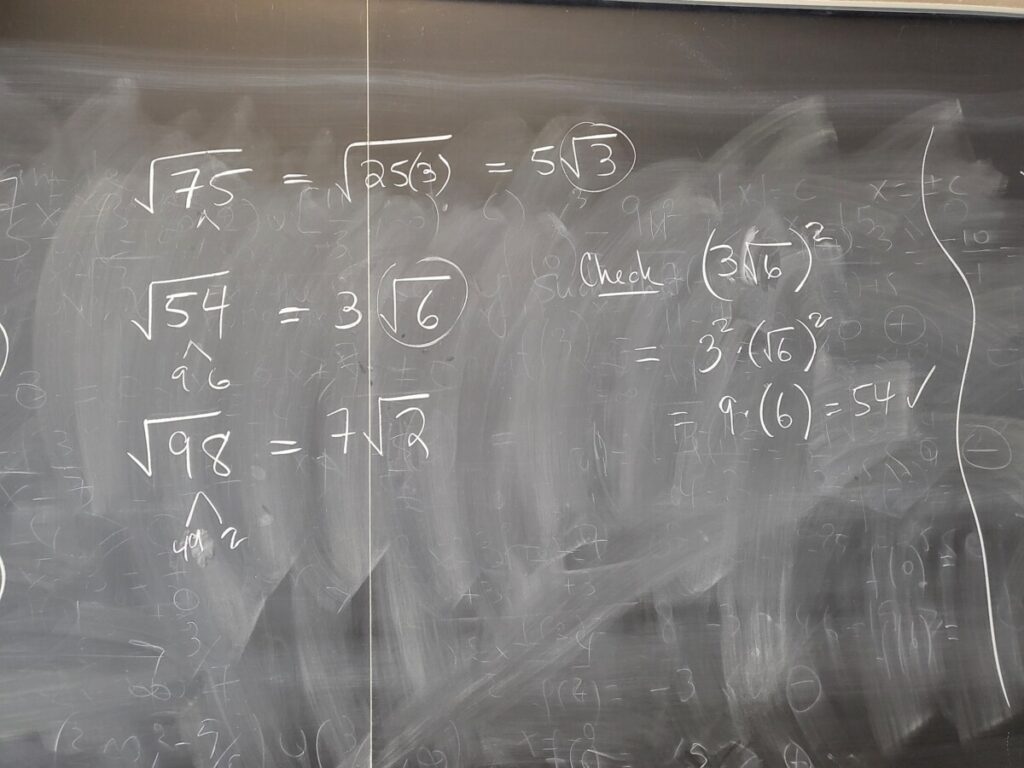


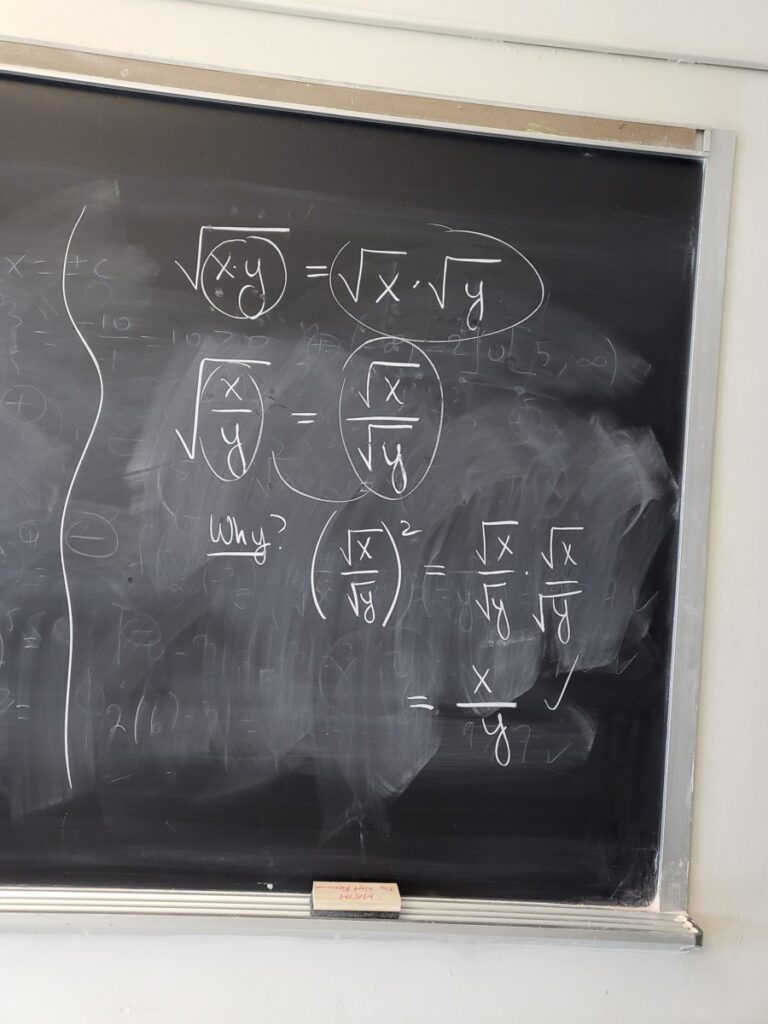
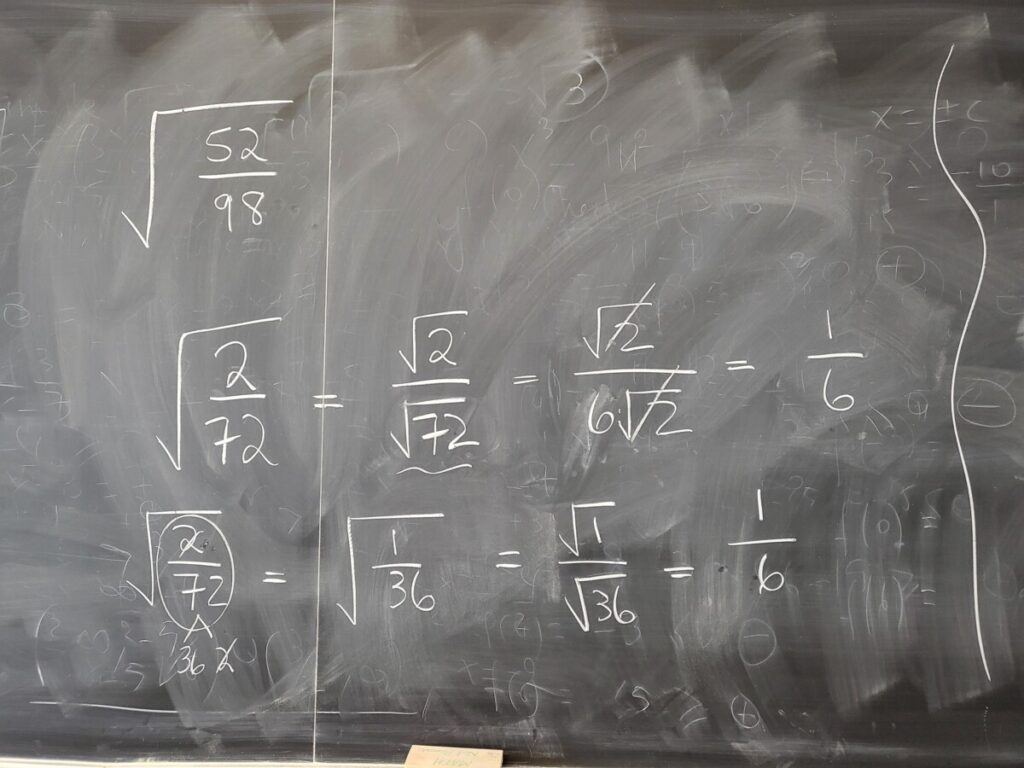
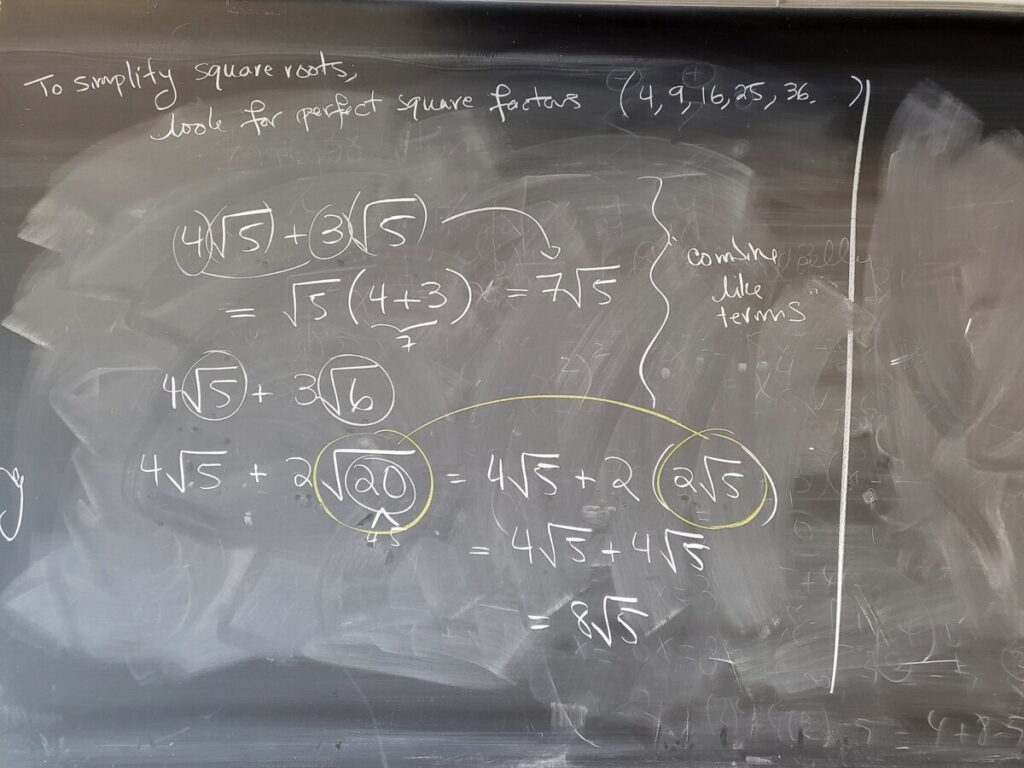
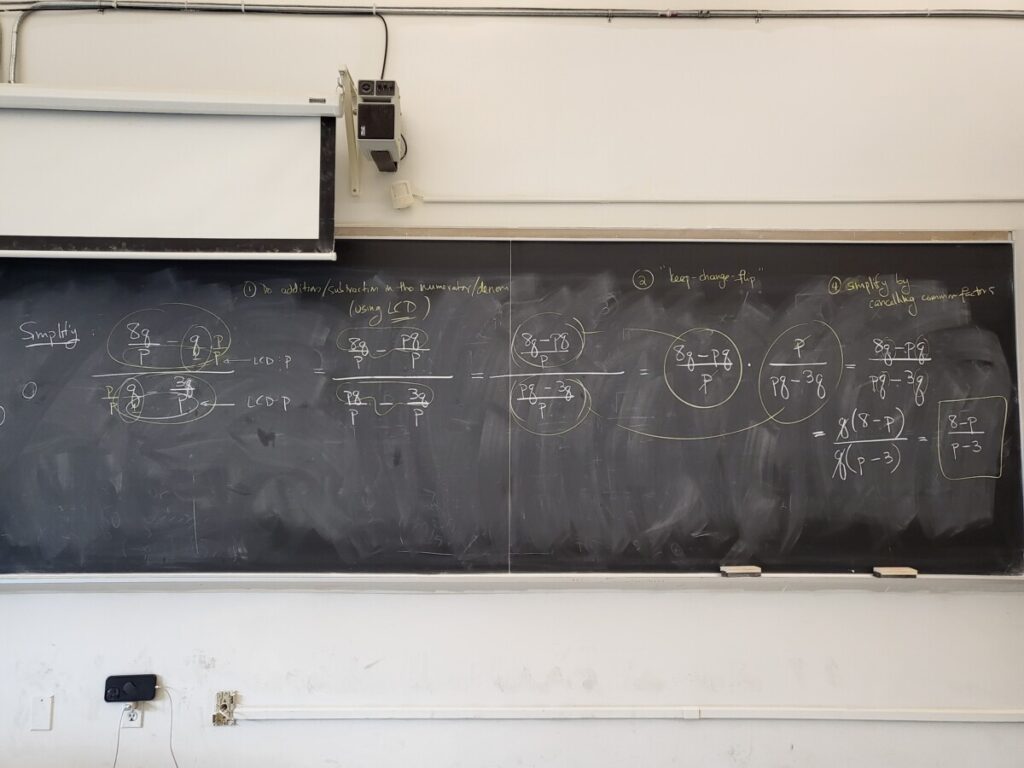



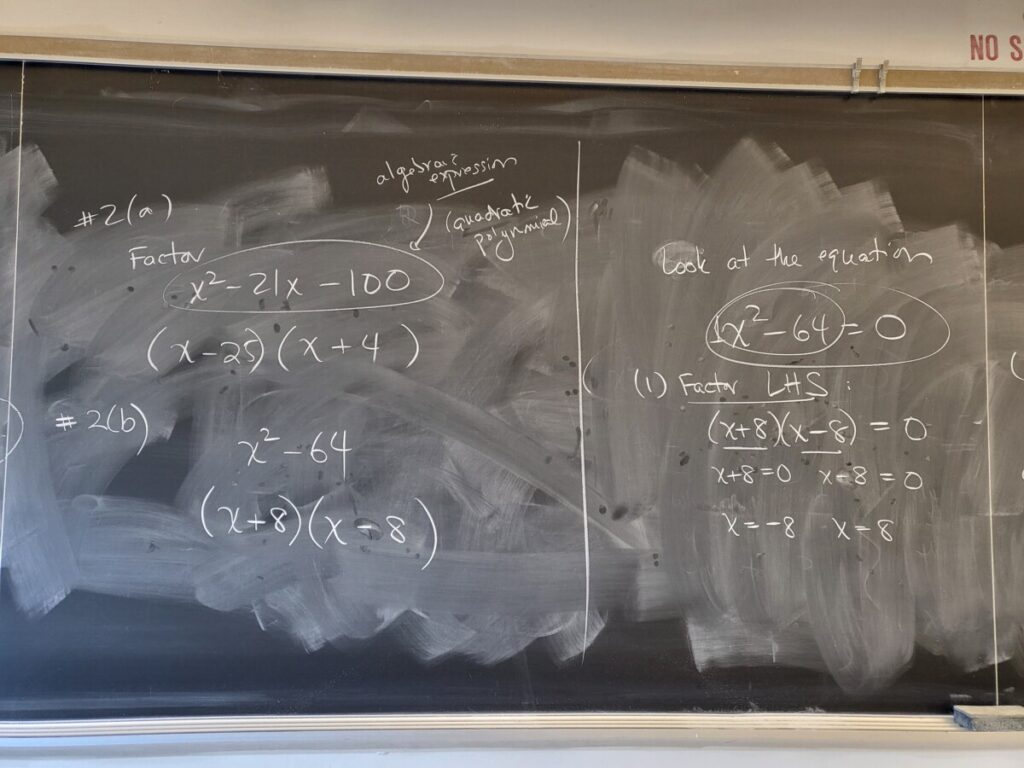





Recent Comments