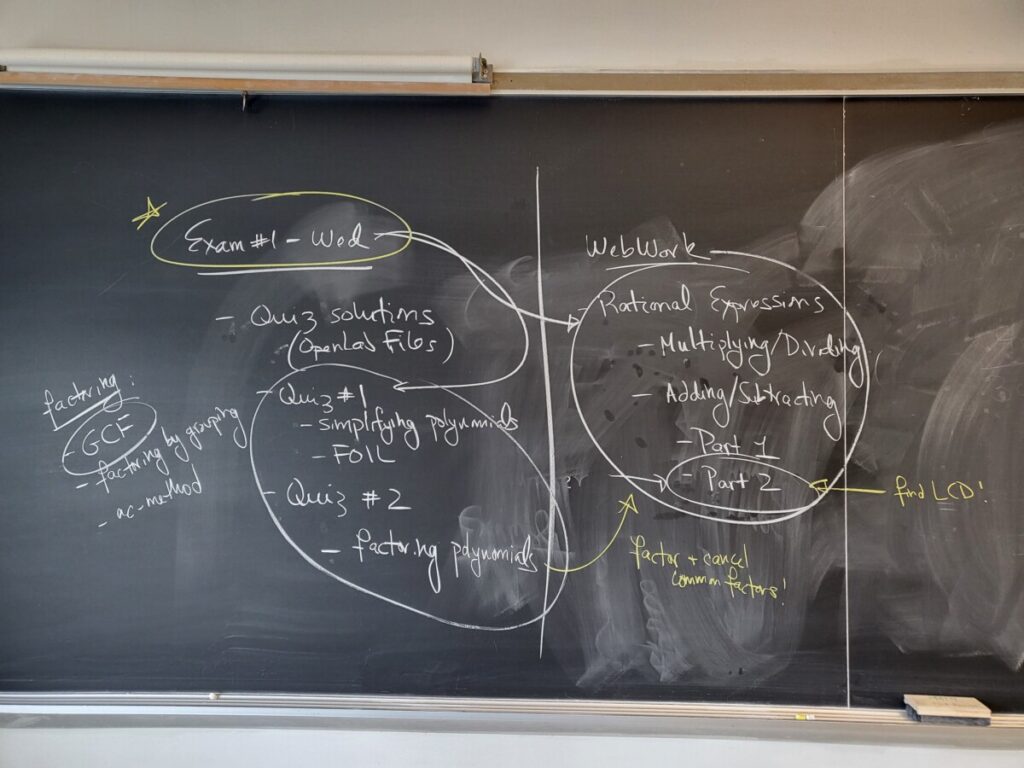
Our second midterm exam will be next Wednesday (Wed April 17). Please continue working on the open WebWork sets, especially the exercises listed below; you should also review the exercises listed below from earlier WebWork sets. The best preparation for the exam is to write out solutions to the WebWork exercises listed below.
Also listed below are some exercises from the MAT1275 Final Review sheet, which is available as a pdf on the Math Department website here, and also on our OpenLab Files. You can also write out solutions to these Final Exam Review exercises to review for this exam (and to prepare for the final exam!)
You should also review your class notes and the Class Recaps here on OpenLab, since we did most of these WebWork examples in class–see Class Recaps #12-22.
You should also review the Quiz #3 and Quiz #4 solutions, which are available on OpenLab Files. You can also review relevant examples from the textbook.
(I will update the list below with specific textbook examples to review.)
Here are the topics and relevant exercises/examples to review:
Simplifying complex fractions:
Quiz #3
WebWork: “Rational Expression-Complex Fractions 2” #1-3
Final Exam Review: #3
Multiplication and division of complex numbers:
Quiz #4
WebWork: “Complex Numbers” #4-7
Final Exam Review: #5
Solving quadratic equations:
via factoring and the zero product property:
WebWork: “Quadratic Equations – Zero Product”: #2-6
(review factoring of quadratic expressions from Exam #1 if necessary)
via completing the square and the square root property:
Quiz #4
WebWork”Quadratic Equations – Square Root”: #2-6
WebWork: “Quadratic Equations-Completing the Square”: #3-5
via the quadratic formula (including simplifying square roots):
WebWork: “Quadratic Equations-Quadratic Formula”: #1-3
Final Exam Review: #1
Graphs of quadratic equations (parabolas):
WebWork: “Graphs of Quadratic Equations”: #7-9
Final Exam Review: #2



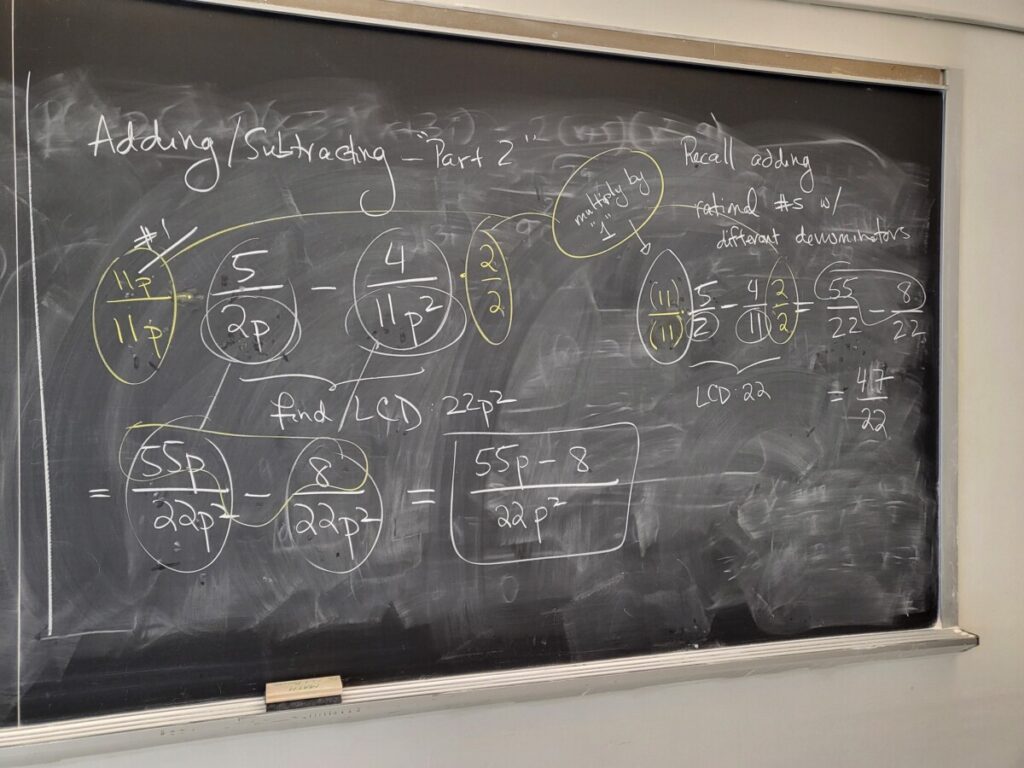




Recent Comments