Announcements
WebWork schedule:
- Rational Expressions-Complex Fractions 1 – due Mon March 18 (Sec 1.3.4)
- Radical Expressions-Simplifying – due Mon March 18 (Sec 1.4.2)
- Rational Expressions-Complex Fractions 2 – due Wed March 20 (Sec 1.3.4)
- Radical Expressions-Adding and Subtracting – due Fri March 22 (Sec 1.4.4)
Topics
We studied “radical expressions”, i.e., expressions involving square roots, and went through another complex fractions example.

We started by discussing what the square root of a number is:

In order to simplify square root expressions, we primarily use the following “product property” of square roots (“the square root of a product is the product of the square roots”):
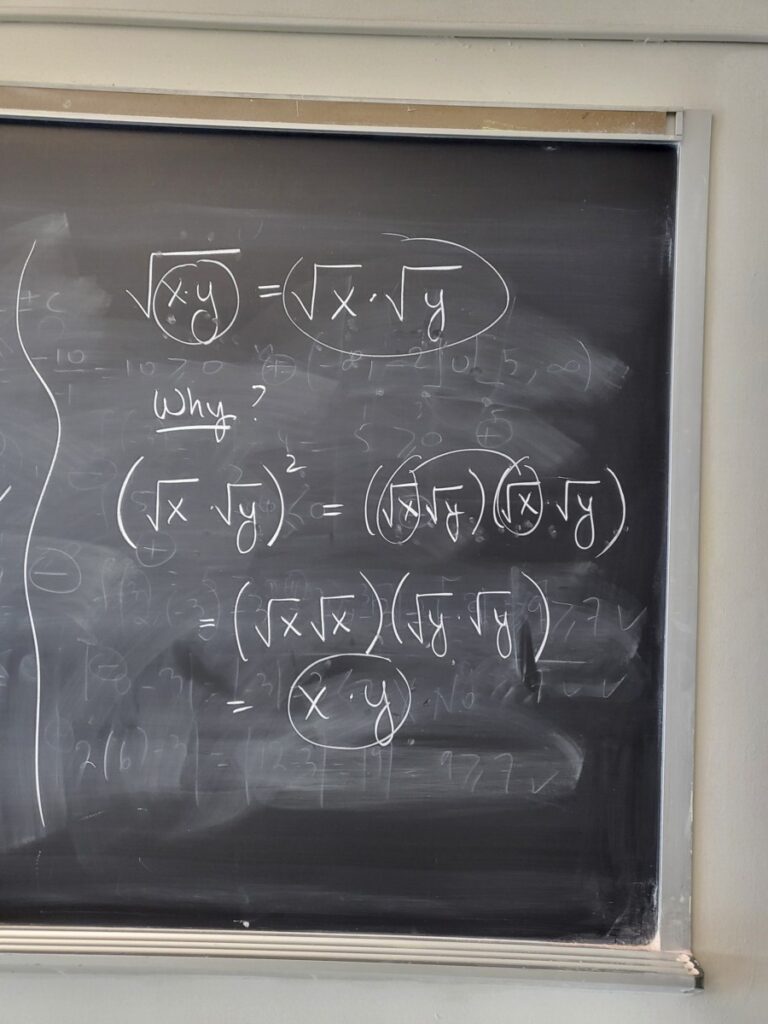
(However, note that this does not work for the square root of a sum, as we can see from simple examples:

We can use the product property of square roots to simplify square root expressions–the strategy is to look for “perfect square factors” of the number (or the expression) inside the square root:

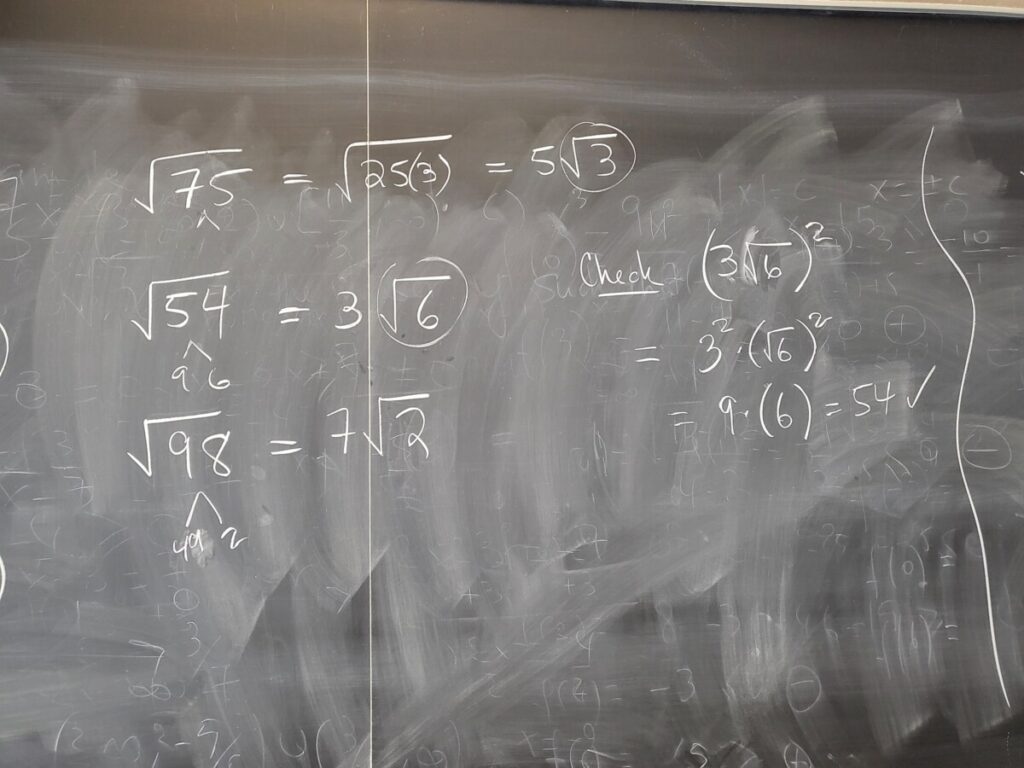
We use the same strategy for square roots involving algebraic expressions:

We did some exercises from the WebWork using this technique:

We can also simplify square root expressions involving ratios, using a similar property:
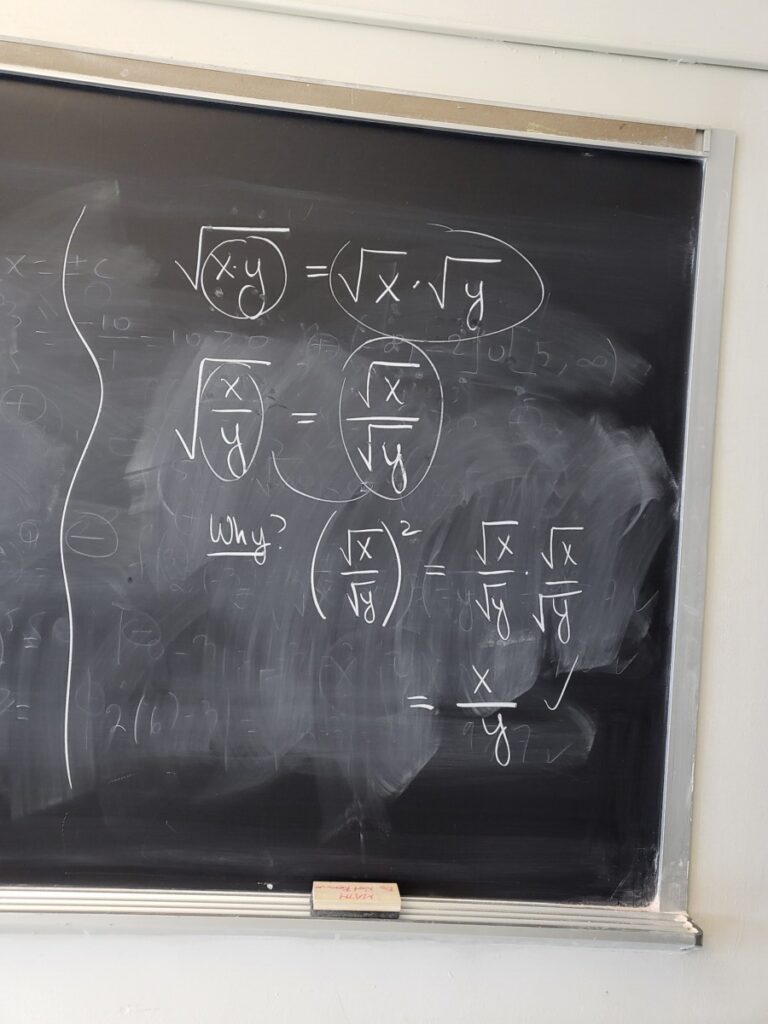
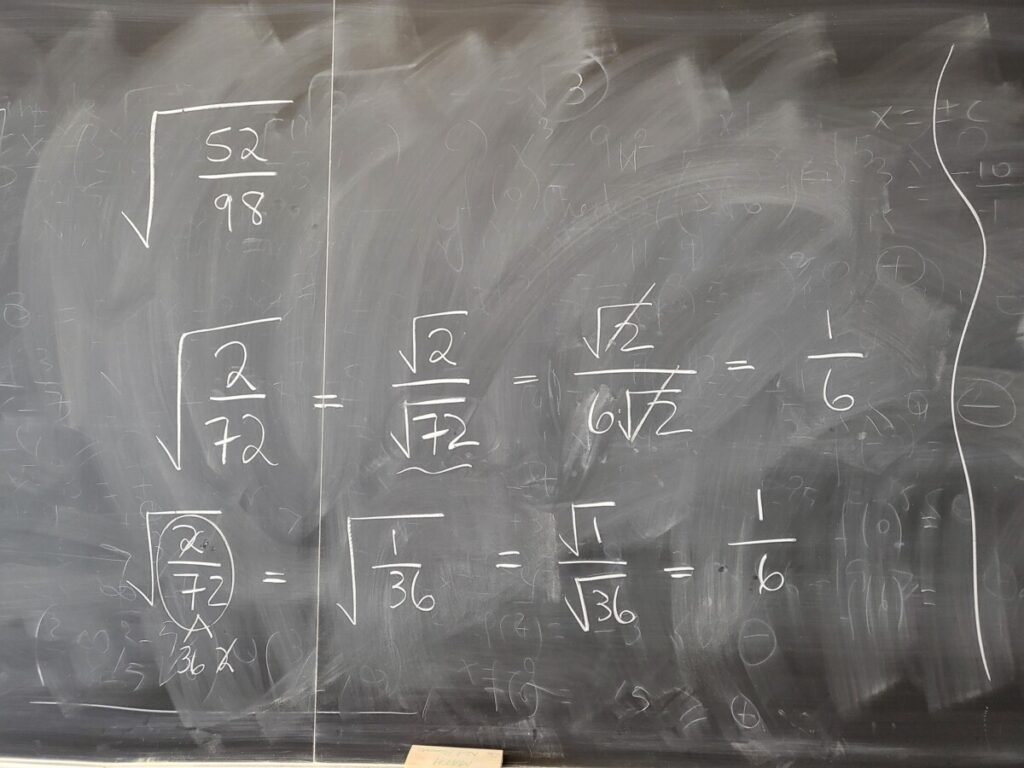
We then introduced how to add/subtract square root expressions–here we treat square roots of the same number/expression as “like terms”:
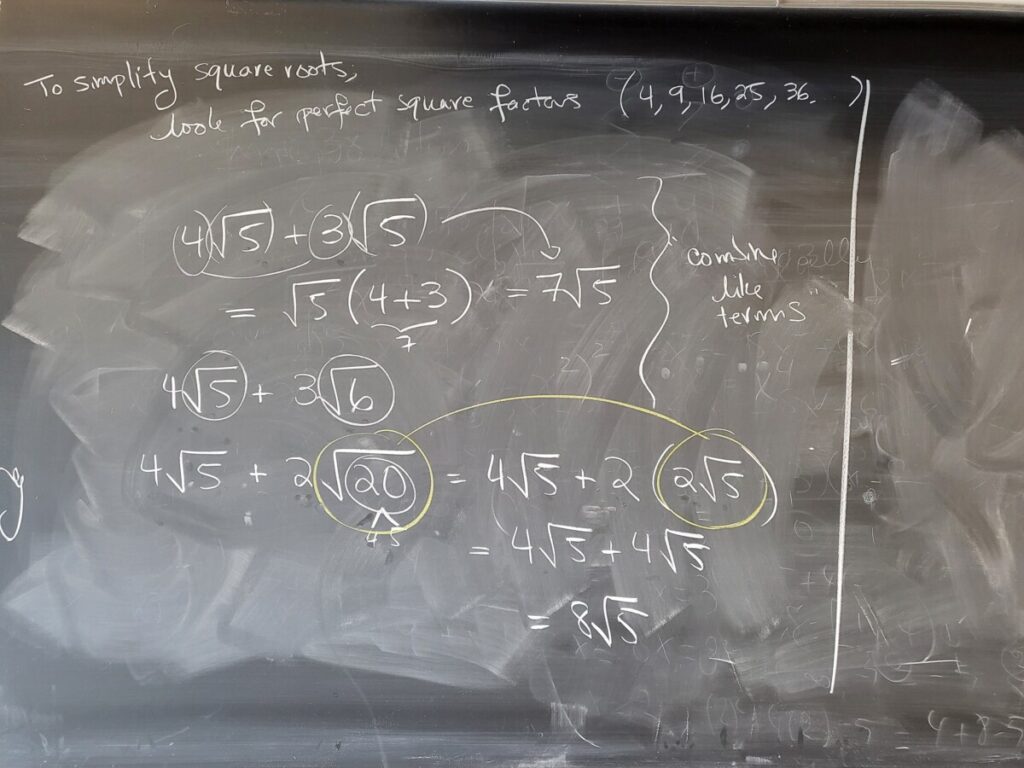
Finally, we returned to complex fractions, and did an example from “Complex Fractions Part 2”, which involve multiple steps:
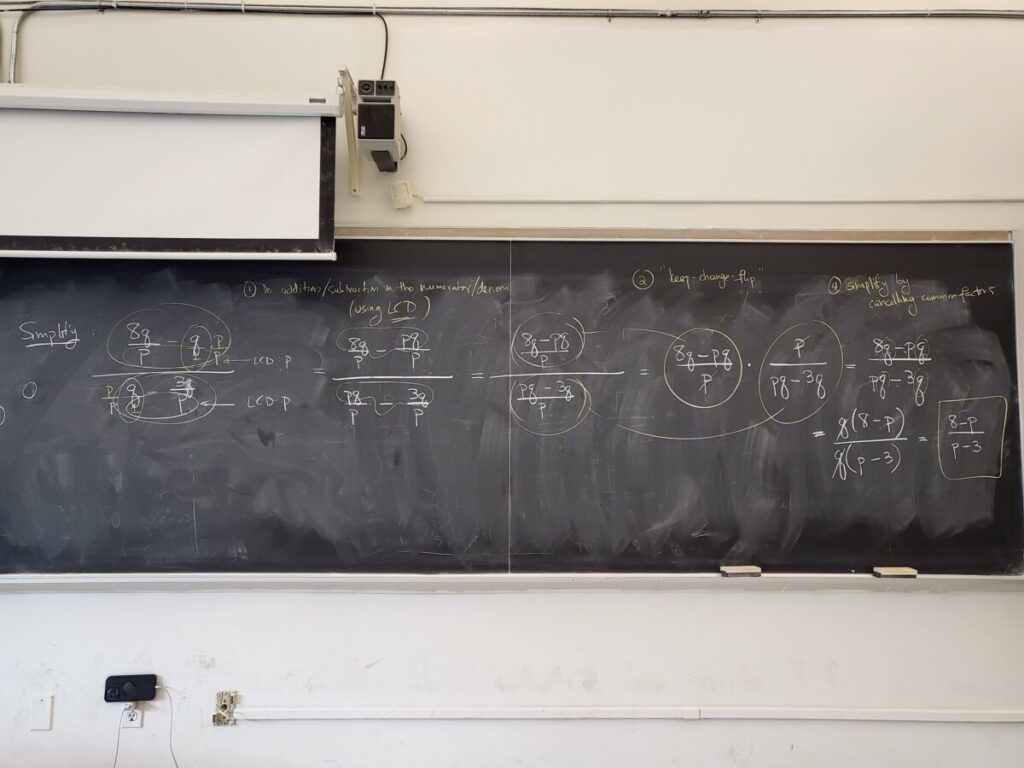



Recent Comments