Announcements
WebWork:
- Radical Expressions-Multiplying – due Thurs March 28 (Sec 1.4.4)
- Radical Expressions-Complex Numbers – due Mon April 1 (Sec 1.4.6)
Topics
We revisited “complex numbers” using the new number symbol “i” to represent the square root of -1. A complex number is anything of the form “a + bi” (where a and b are regular real numbers). We call “a” the real part and “bi” the imaginary part.
(Complex numbers are covered in Sec 1.4.6 of the textbook, where you can find additional examples.)
We then reviewed addition/subtraction of complex by “combining like terms” (here the real and imaginary parts of the two given complex numbers):

For multiplication we use “FOIL”–together with the fact that i^2 = -1 in order to simplify:
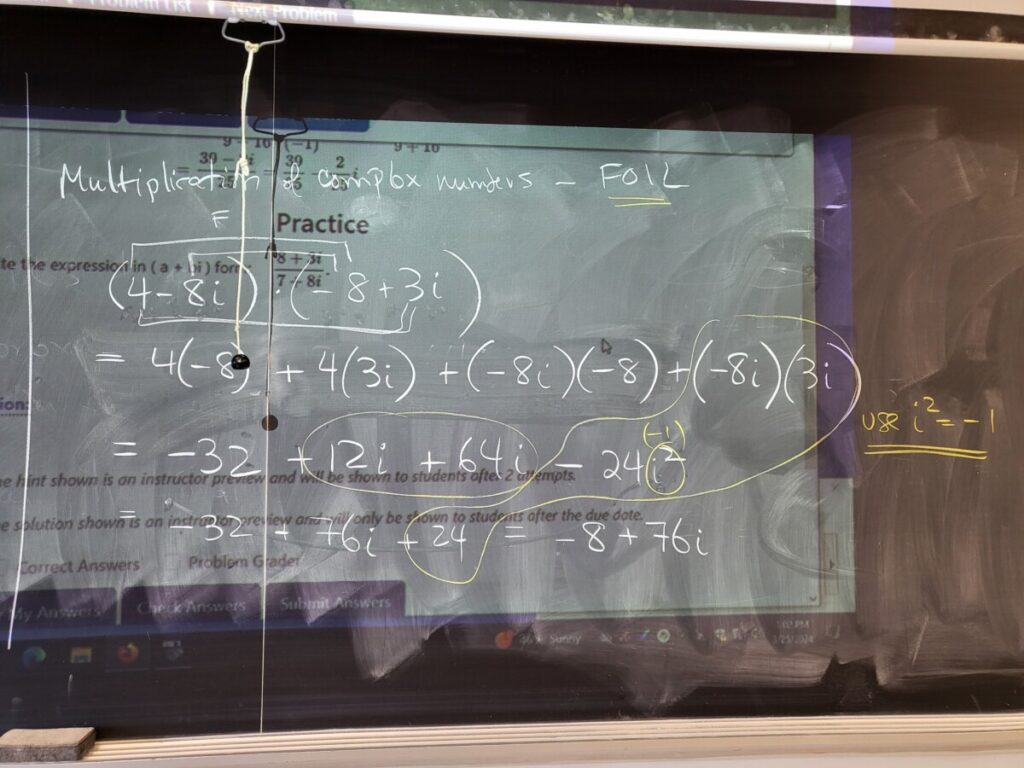
We then did a multiplication example from the WebWork which introduced the idea of two complex numbers which are “complex conjugates”–they differ just by the sign between the real and imaginary parts–in which case their product is just a real number:

Next time we will show how to use this feature of the complex conjugate to do division of complex numbers, as explained in the WebWork set:




Recent Comments