Announcements
WebWork:
- Radical Expressions-Complex Numbers – due Mon April 1 (Sec 1.4.6)
- Quadratic Equations-Square Root – due Wed April 3
Topics
We covered division of complex numbers, and then shifted to discussing quadratic equations and how to solve them.
For division of complex numbers, we first reviewed the idea of complex conjugates:
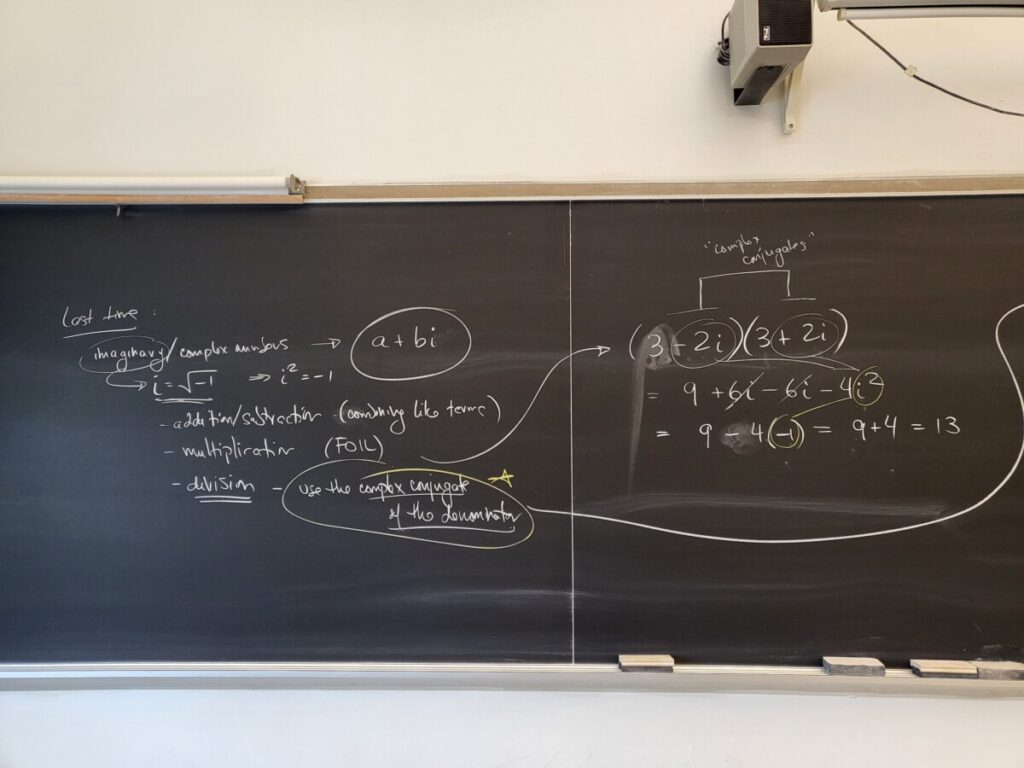
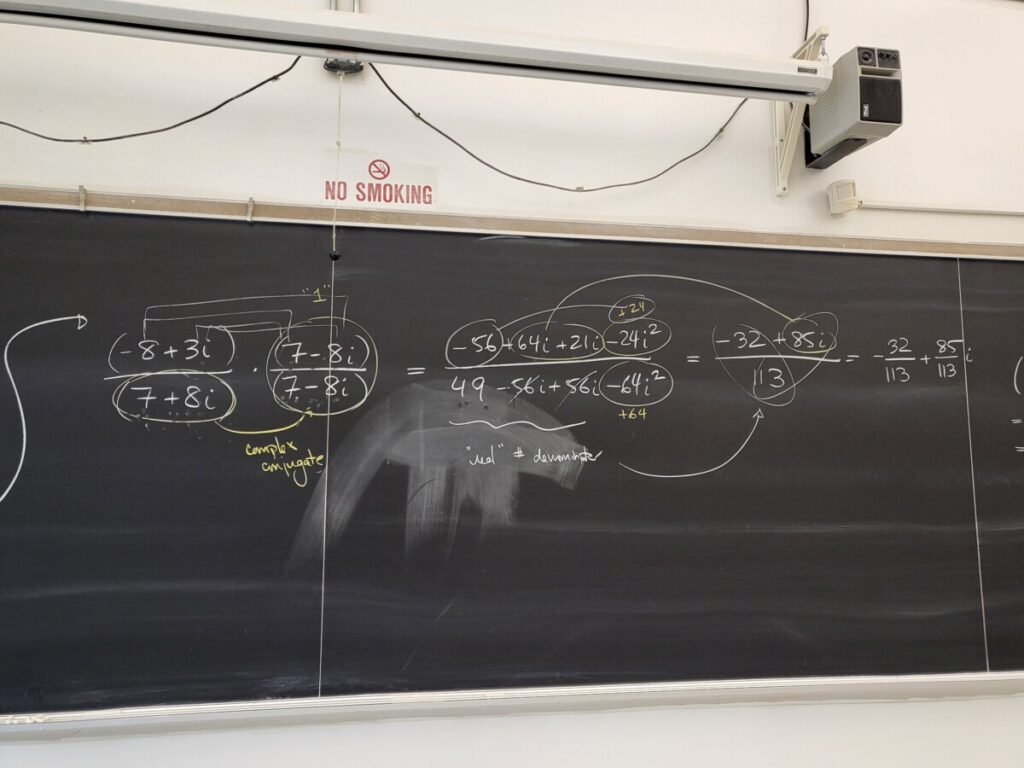
We can use the complex conjugate (of the given denominator) to do division of complex numbers:
We then discussed quadratic equations. We showed how we can solve certain quadratic equations by factoring (and using what’s called “the zero product property”–see Sec 2.2.1):

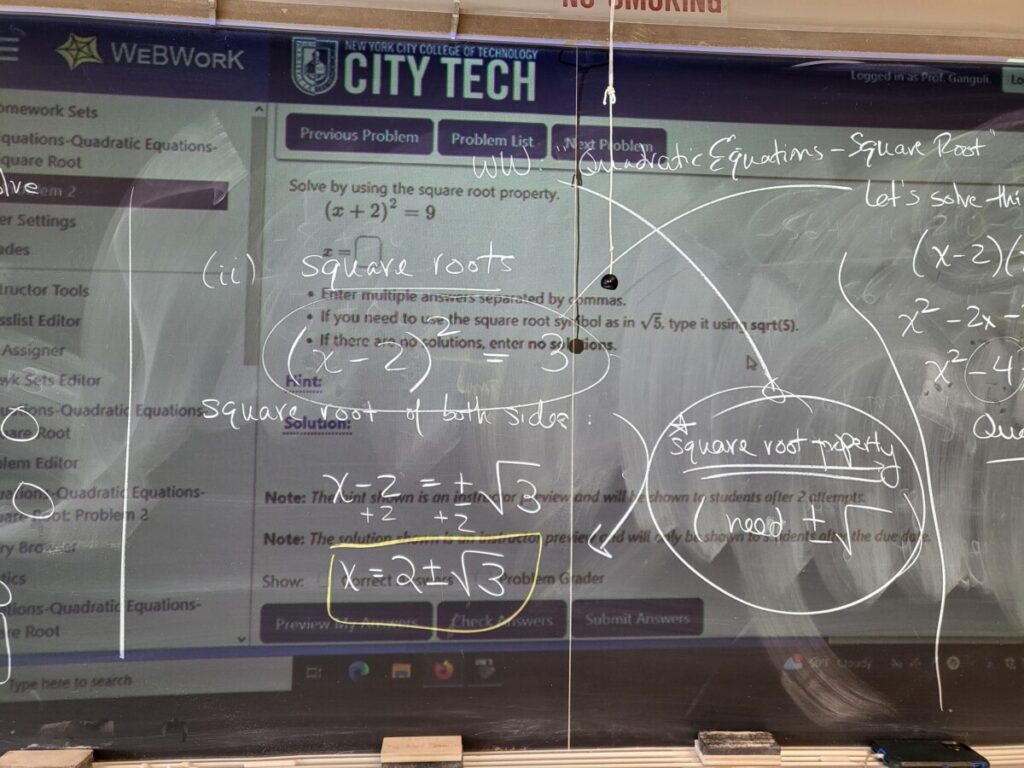
If the quadratic equation is given in a certain form, we can solve via square roots (using what’s called “the square root property”, i.e., that we need to account for both the positive and negative square roots–see Sec 2.2.2):
We also showed how we can solve this equation using the quadratic formula:
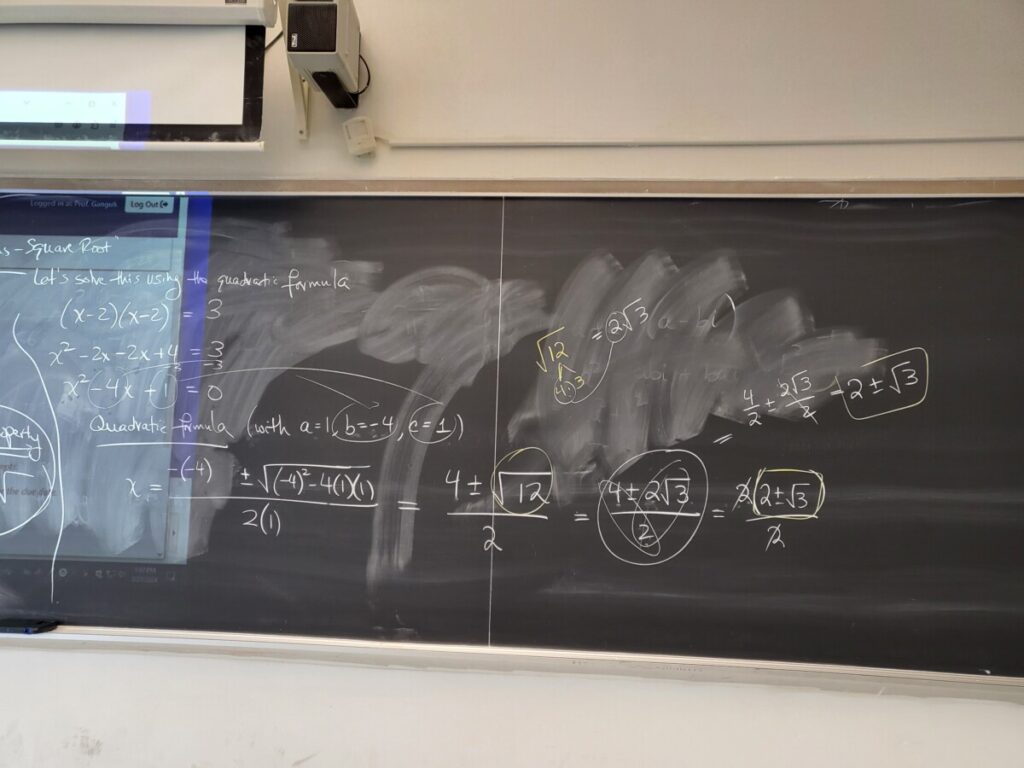
We did some examples from the “Quadratic Equations-Square Root” WebWork:
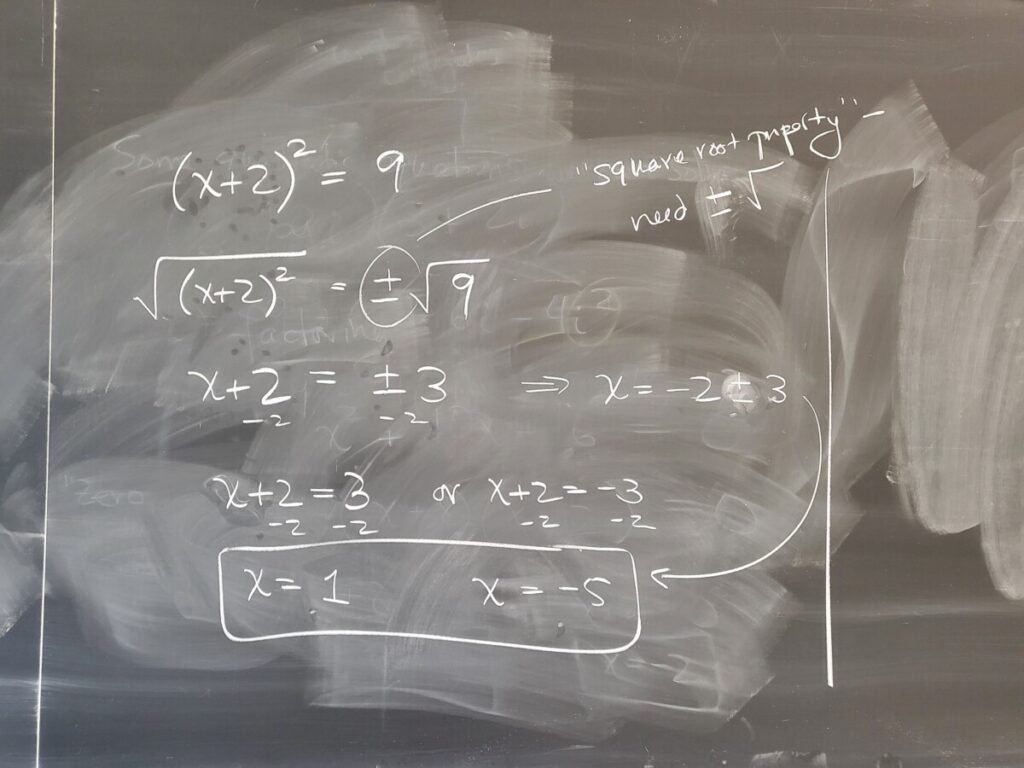

Next time we will discuss “completing the square”, which will show us how the quadratic formula comes from:


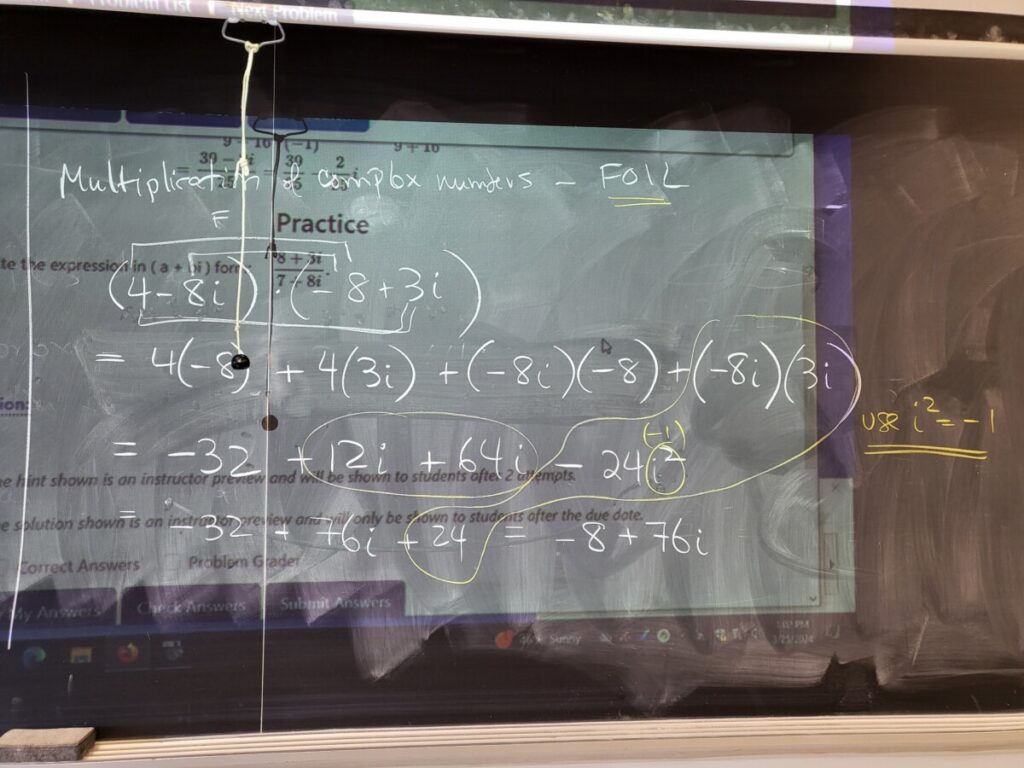




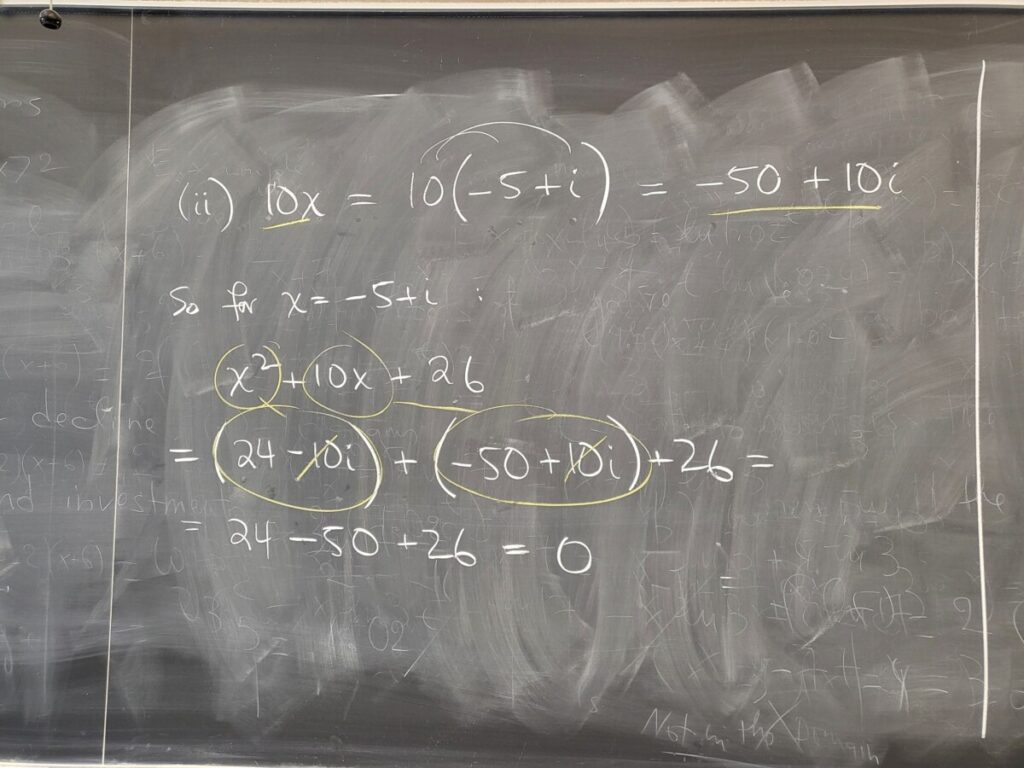
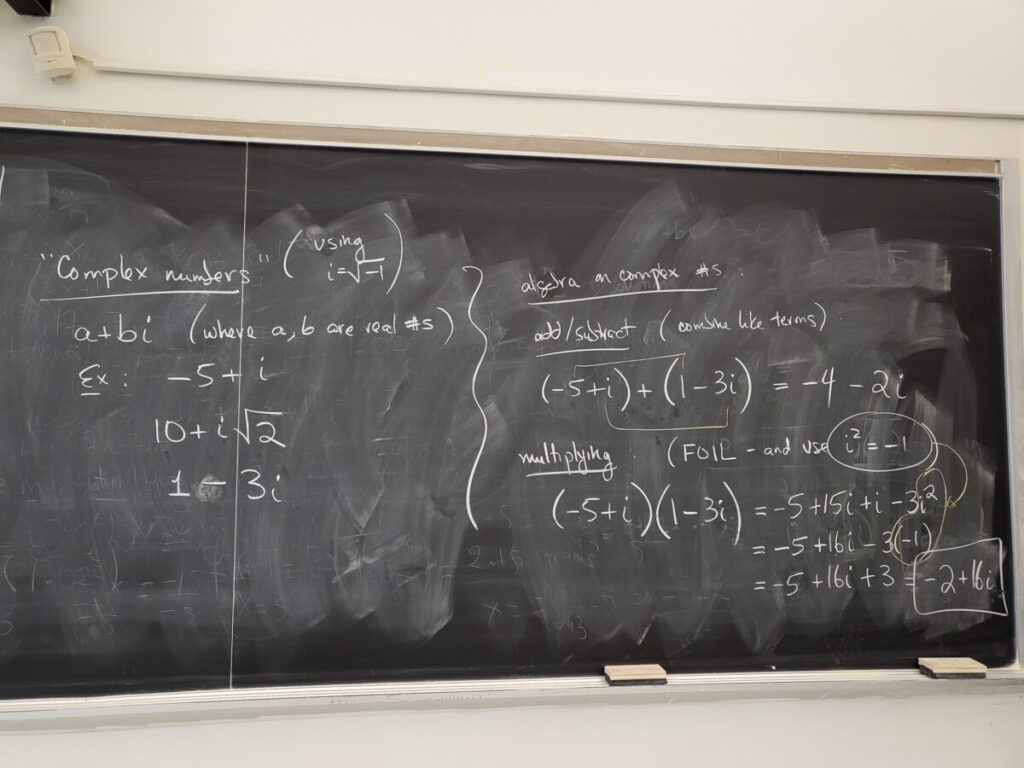



Recent Comments