Your assignment for the next week is to try to prove the conjecture that your group created in class on Tuesday, 10/14/15. You must spend at least 90 minutes working on this. Trying to prove something can consist of many different activities, such as the following (you do NOT have to do all of these things – you can choose how to spend your time – they are provided for inspiration only).
- coming up with ideas, and testing them out (for example, by creating puzzles and trying to solve them)
- trying to understand what the conjecture says
- trying to solve puzzles that other people created
- trying to create puzzles (and solve them yourself)
- communicating with other members of your group (talking, emailing, etc.)
- trying to write down a proof
- other stuff…
As you work, keep track of what you are doing, thinking, and feeling (this is metacognition – an idea that discussed way back in OpenLab #2). What did you do during the time you spent? Did you create any puzzles? Did you solve puzzles? Did you change your mind about whether the conjecture is true or false? Did you have any new ideas about how to prove the conjecture? Did you have any ideas that you gave up on? How did you feel as you worked – were you frustrated/confused/happy/depressed? Why? Did your mood change along the way?
Assignment (Due Thursday, 11/3/15): Submit a journal of your efforts in the comments below. Your response should be at least 300 words. Describe what you did during the 90 minutes you worked, and express in some way what you were thinking and feeling during the process. Your response can include puzzles (use sketchtoy.com) or other work you did along the way.
Extra Credit. Respond to a fellow student’s comment. Did you do similar things? Different things? Do you have any suggestions for them? Be kind.
GROUP CONJECTURES:







When I was practicing the conjecture for class I was trying to think of ways to draw a rectangle that has diagonals and is also symmetrical. When I was looking at the conjecture I wanted to look at it in both ways, is the conjecture true or is the conjecture false. When I was trying to draw the rectangles I was trying to draw it both ways in which one of the rectangles has diagonals and the other rectangle has a diagonal but wasn’t symmetrical. When I tried proving the conjecture to be correct when with a rectangle having diagonals and also being symmetrical. When I tried using a rectangle that wasn’t symmetrical but had diagonals I found out that you can get 0 solutions or 1 solutions. When I tried doing this with a different picture that wasn’t symmetrical but had diagonals and was a rectangle I also found out that the puzzle has only zero solutions because the puzzle was a little more complicated that the other one I tried doing. I think that the conjecture should be changed to that any puzzle that contains a rectangle that has diagonals and is also symmetric could possibly have zero to 2 solutions but also vice versa. Before drawing the puzzles I believe that the conjecture was already true but when I started testing out the conjecture with different puzzles I found that the puzzles can have zero to two solutions just like what the conjecture was saying. I believe that the conjecture that our group came up with could go both ways because what if someone created a puzzle that was a rectangle having diagonals and not being symmetrical can also have 0 ways to 2 ways to solve the puzzle can this disprove the conjecture or not. I believe that everyone can have their own opinion about this conjecture whether supporting or going against the conjecture.
we got ourselves a tricky one, I realized that our solutions involve triangles and our rectangle itself involves a lot of triangles, so it’s solutions may vary. I’m very certain that you will never get 1 though.
My group’s conjecture states, “A starting point must have more than one bridge connecting to it if the puzzle has a solution. Well, obviously each starting point A, C, D, and B all have more than one bridge connecting to it, so I assumed that starting from anyone of these points will lead to a tour only walked once. First, I noted that the points/vertices A, D, B have one thing in common, they all have three legs/sides that extend from them and at least one of those legs will lead you to point C. Also, point C is the only point in which there are five legs extending from its point. So, in order to attempt to prove my conjecture I decided to start from point C, because it seemed like it will be more probable to find a solution for the tour. Whereas, point A, D, B will have a number of possibilities but not nearly as much as C. Starting from point C using paths p to A and taking each possible route which led me to a total of thirteen routes all of which led me back to a path already taken. I soon realized that there is no path to take that will not repeat. Consequently, I begin to look at the puzzle differently and noted that it is symmetrical. Therefore, I infer that each point stemming from C will reflect the same amount of possibilities that will lead you to a dead end—resulting in an incomplete tour. Thus, in this case of connecting sides to four points, there will never be a successful tour where no paths cross—it is impossible! Henceforth, my group’s conjecture of a starting point having multiple possible choices has been proven to be false, so this could be considered a counterexample of why it will never work making the puzzle unsolvable with no possible solution.
As we work as group one of us come with idea or lets called a conjecture it says if you have a shape with two corner with odd degree its not possible to solve. since then i try to understand what he means since i did not take any courses related to graph theory , what i hear from he him something capture my mind what he mean when he say odd degree so i decide to go and look for what exactly he mean , since I am a knid of person i will want to knew exactly what is going on , I watch a lot of videos related to graph theory and what is even and odd degree exactly , going back to watch more videos about the seven bridges walking tours , Leonhard Euler solultion for the problems of the seven bridges , back to our conjecture , now i really understand it much more clear, and i still feel i need to look more for more information to be convinced. still working more to under stand the topic good . what is the meaning of vertices , what we mean when we said odd vertex , now i knew that odd vertex is a vertex whose degree is odd , and what is A graph Agraph consists of one or more vertices attached by edges.Frequently we draw he vertices as points and the edges as line segment or curves , an edge can attach a vertex to it self this called loop. I will say this Assignment i got too much benefit from it , and Iam trying to improve my self to the point i will be happy.
Yep at first when I saw you write “an odd degree” I was thinking in terms of the angles. What you’ve taught me is that odd degree could be the amount of vertices at a specific corner or angle. At first it probably wouldn’t have worked but it does since we added the enclosed shape part. If the shape wasn’t enclosed then our conjecture would of ended up being extremely tricky.
Sorry about not being clear enough, I should have done sample drawings in front of you to illustrate what I was talking about. As for degrees; a degree in this context is the number of lines stemming out of a corner. I’m not talking about the angle.
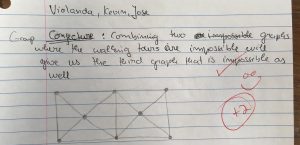
Few days ago, my group and I came to the conclusion that combining two graphs where the walking tours were impossible,gave us the third graph that was impossible as well.
However,I thought that maybe we came fast to that conclusion.So,I tried to find if there exists any possibility such that the walking tour in the graph would be possible.First, I started from the first point, and I went to all ways,and still the walking tour would not pass in one line,so it was impossible .Then, I thoughy that starting from other points will give me different answer.Do,I took every single point as a starting point,and still the walking tour was impossible.After that combining two graphs gave me a graph where the walking toir was impossible,I thought to add another graph.Even though that thiss time I changed a little bit my conjecture from combining two graphs in combining three graphs, I was still getting a graph where the walking tour was impossible in each point that I started.Then I added another graph next to the third one,and I was getting the same answer.So,I came to the conclusione that as many graph where the walking tour is impossible as we add,we still get the same answer. After, I added another graph under the first one,and then another one under the second one, and under the third one,and I got the same answer.
So, in every way that I tried to put same graphs next and under to each other, our conjecture came up to be true, that combining graphs where walking tours are impossible will give us a graph that is impossible.At this time our conjecture is true for more than two combined graphs.
I had three main things I wanted to get done within the 90 minutes. 1) Write my conjecture over and really think about what it says. 2) Re-examine the cases that follow my conjecture from the bridges and tunnels open lab assignment and see if it satisfies my conjecture. 3) Try to prove my conjecture fails and if so, fix it up a bit. I spent some time really analyzing what the conjecture said. I’m a bit of a fan of the work we did in class with quantifiers so I wrote it in terms of quantifiers. I made it into a conditional statement and even found the negation to it for my exercise 3 later on. For number 2, I re-solved numbers 3, 4,5,6,7 from our open lab assignment involving the bridges and tunnels tour to make sure it was 0 or 2 solutions. I think there are only 2 for the all except 3, 4 which are 0. I wrote out the cases and realized their 2nd solution is just the opposite letters of each other. If a square is square ABCD and a solution shows something like abcd, then you can swap the corresponding letter and create a solution badc. My final step was to prove it fails if I can, and I did because I realized I need to create a triangle in the beginning to find a solution, if its symmetric, then that triangle must also be on the opposite side. If you put 2 rectangles together, then you take the option of one triangle out of the picture causing it to be reduced to just 1 solution. It even fails when you add one more connection (for a total of 2 connections + the actual rectangle(s)) because you can get a total of 4 solutions. Since I proved it false, I decided to edit my conjecture to, if a pathway consists of a rectangle with 2 diagonals with 1 additional pathway and the pathway is symmetrical, then there can be either 0 or 2 solutions.
A conjecture is a statement regarding some rule or fact, that you can benefit from, that gives you a hint of how a game works. My groups conjecture was “If there is an enclosed shape with only 2 corners of an odd degree then the puzzle is possible. You first start at one corner of an odd degree and would end up at the other odd degree corner. On the other hand if you have an enclosed shape of more than 2 corners of an odd degree then the puzzle would be impossible to solve”. I’ve worked on this conjecture multiple times and was able to actually prove it. My first step was to make 2 shapes with the same shape, a square, and then to give each different odd degree corners in terms of number. The first square had only 2 odd degree corner and was easily solvable. The second square however had 4 which made this puzzle impossible to solve. I clearly couldn’t stop there since that was only just one example. I decided to play around with the lines within the shape turning odd degrees, I created, into just even ones, leaving just 2 odd degrees, but having the rest of the corners an even degree. The puzzles ended up still being possible which just completely caught me in awe. It was as if I was learning an answer to the universe. I then tried shapes with circular lines but that still had 2 corners of an odd degree. The conjecture still held and I was able to realize that it was a solid and valid conjecture when it came to bridge puzzles in an enclosed shape. One theory from the conjecture that made some of the complicated puzzles I created easily solvable was, the part that stated, that if you start from one corner of odd degree then you would end up at the other corner of odd degree. By visualizing the theorem that way I was able to complete the puzzles in a fast paced fashion. Before my 90 minutes was up I was able to prove this conjecture repeatedly over and over again. I believe that this conjecture works since it correlates to having and odd number of bridges in an enclosed shape to have a solvable puzzle. If you had 2 odd degree corners in an enclosed shape then you would have as well an odd number of bridges leaving you with a solvable puzzle.
I began with brainstorming random conjectures in my head. When we were tasked with creating problems to submit, I detected a pattern of unsolvable problems. This mainly stemmed from the initial bridges tour and I realised why I added another route to “solve the problem”. I ended up changing the walking tour by changing the number of odd degrees in favour of more even ones.
I also noticed when Professor Reitz drew a random shape on board that I immediately looked for any corners with “3” (later to define as odd) corners. Once I realised that there were no more than 2 of these types of corners, I hypothesised that that problem could be solved; just start at that odd corner and work your way to the other one. I figured it out in a couple of seconds and I realised I might be on to something.
From sketching numerous shapes and pondering about them in my head, I realised that there was some kind of “rule” (later to become our conjecture). We had to either start and/or end on a vertex of an odd degree.
I initially stated that it must be an enclosed shape but I forgot that any vertex that’s “sticking out” is a vertex of degree 1 (as in an odd degree).
http://sketchtoy.com/67618926
http://sketchtoy.com/67618930
This drawing represents an imaginary problem with two sides of degree 3; from the animation you can tell I have to start at either odd degree-vertices in order to solve the problem. The red dotted line represents any number of even degree vertices.
I’m refining my conjecture to: “any problem with more than 2 vertices of an odd degree is unsolvable, as you must start and end at an odd degree-vertex”.