The assignment below is due BEFORE CLASS on Thursday, October 8th (it is essential that you complete it before class, as we will be doing a class activity building on the assignment).
We are going to play a game creating walking tours of cities with bridges. We begin in the city of King’s Mountain, which is built on four land masses – both shores of a river and two islands in midstream – connected by a total of seven bridges (shown in green).

EXAMPLE 1: Can you create a walking tour of the city that crosses every bridge exactly once? You can begin anywhere you like, and end anywhere you like, as long as you cross each bridge just once.
Background – Graph Theory
We can simplify the picture of King’s Mountain to make it easier to deal with:
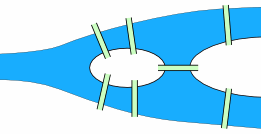
The key elements of the map are the four land masses (let’s label them A, B, C, and D) and the seven bridges (p,q,r,s,t,u and v) (thanks to mathisfun.com for the images):
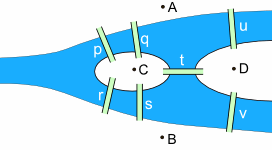
For the purposes of our problem, we can simply think about each land mass as a point (A, B, C, and D), and the bridges as lines connecting the points (p,q,r,s,t,u and v) – like this:
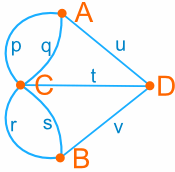
We call this kind of picture a graph – the points are called vertices and the the lines are called edges. Our goal of finding “a walking tour that crosses each bridge once” is now matter of tracing out all the edges without lifting our pencil (and without repeating any edge).
Assignment, Due Thursday 10/8 (beginning of class)
Warm up (This Warm Up is just for practice – you do NOT need to submit your answers – see below for the three-part Assignment to be submitted). The following examples build on EXAMPLE 1 above.
WARM-UP EXAMPLE 2: If you are given the freedom to build one new bridge in King’s Mountain (“make one new edge in the graph”), can you do it in such a way the walking tour becomes possible? Do it!
WARM-UP EXAMPLE 3: If you are given the freedom to destroy one bridge (“erase one edge”), can you do it in such a way that the walking tour becomes possible? Do it!
WARM-UP EXAMPLE 4: Construct walking tours for each of the following graphs (or decide if it is impossible).
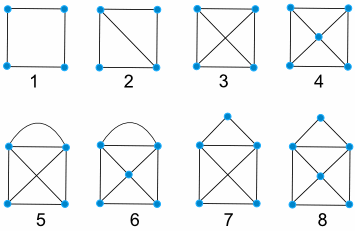
Assignment. Your assignment has 4 parts.
PART 1. Leave a comment responding to EXAMPLE 4 (above), telling us for each one of the 8 graphs whether a walking tour is possible or not. You only have to state whether it is possible or impossible for each one.
PART 2. Challenge your friends: Now it’s up to you to build your own graph, and challenge your classmates to construct a walking tour (or to determine if it is impossible). It can consist of as many points as you wish, and as many bridges (edges) connecting them. You MUST label your points “A, B, C…” etc. When you’re finished, decide for yourself if a walking tour crossing each bridge exactly once is possible. Remember, the most challenging puzzles are the ones where the answer is difficult to determine. Post two puzzles in the comments. See the note “POSTING YOUR PUZZLE ONLINE” below for instructions on how to draw and share graphs online.
PART 3. Solve a friend’s puzzle. Leave a response to a friend’s posted puzzle, giving a solution. TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER.
Example:
Here is a puzzle: http://sketchtoy.com/65962726
Here is a solution: (start at A) – A, C, B, A, D, C
PART 4. The third part of your assignment is to write a short paragraph (at least 3 sentences) responding to the following prompt. Be sure to respond to each part:
Writing Prompt: Did you enjoy this assignment? Why or why not? Describe a connection between this assignment and our work in the class. (If you don’t believe there is a connection, try to imagine why we are doing this). Leave your response in the comments.
POSTING YOUR PUZZLE ONLINE. I recommend the site sketchtoy.com – it allows you to draw something, then click “SAVE” and get a link to your drawing. You can post the link in a comment, and we’ll be able to click on it and view your drawing. Don’t worry if it’s not pretty! For example, here is a graph that I drew (can you find a walking tour that crosses all edges?): http://sketchtoy.com/65962726



I. 1-Yes, 2-Yes, 3-No, 4-No, 5-Yes, 6-Yes, 7-Yes, 8-Yes
II. http://sketchtoy.com/65986088 http://sketchtoy.com/65986084
III. Waiting for others to post their work. Cannot currently see any other student’s work to solve.
IV. I rather enjoyed this assignment. Anything to do with logic puzzles is usually pretty entertaining for me. In this assignment we are trying to to find a list of non-repetitive edges represented as a list of points. Points may repeat, but edges may not. This is related to counting, which we are doing in class, seeing as we’re counting the edges. We are also creating specific lists, as we are doing with combinations and permutations in class. We are also finding combinations of points and edges to obtain a specific goal, similar to how we use combinations and permutations of sets and lists to obtain a specific goal (“combinations” in the first part of this sentence is meant to be used in the standard English definition, not the mathematical).
http://sketchtoy.com/65986084
SOLUTION: ( Start at A) – A,B,C,B,D,B,A,B
Hi, Justin, I think the first one has no solution. For the second one, one of the possible solution is ABDBABCB.
Justin – thanks for being first to post. Great connections with our work on counting!
1. YES
2. YES
3. NO
4. NO
5. YES
6. YES
7 .YES
8. YES
http://sketchtoy.com/65986303
http://sketchtoy.com/65986326
I enjoy this game a lot and I have fun doing it. however, it will take long time to do it since I have to create non-repetitive edges but it helps me to think logically. I think it is relate to today’s lecture permutation.
Here is puzzle: http://sketchtoy.com/65986326
Here is solution: DHFAGJEIHBFGCJID
Hi, Xiong, I guess no solution for the first puzzle. For the second one, the possible solution is AGJEIDHBFACEDBA.
Very nice puzzles!
1. Yes
2. Yes
3. No
4. No
5. Yes
6. Yes
7. Yes
8. Yes
http://sketchtoy.com/65990555
http://sketchtoy.com/65990586
I really enjoyed this assignment and how we got to work with the different puzzles and try and solve them. The goal of the puzzle is to not repeat a side (bridge) that you go through and try to complete going through all of them. While working with these puzzles I found that there were various way in which you can start and cross the different bridges and succeed getting through all of them. I feel that this assignment relates to the class by having us not repeating paths and by having various options as a result just like the problems we have been working on in class.
I like that your puzzles are symmetrical! (But this doesn’t necessarily help me solve them…)
Part 1
1- YES, 2- YES, 3- NO, 4- NO, 5- YES, 6- YES, 7- YES, 8- YES
Part 2
http://sketchtoy.com/65990621
http://sketchtoy.com/65990624
Part 4
I had fun doing this assignment actually. I was a little frustrated trying to make my sketch look as perfect as possible (lol) but overall this was a fun assignment. This connects to what we are doing in class as far as creating a non repetitive list of bridges to complete the tour. I’m sure there are other ways to complete the tours other than the ones I found as there can be several non repetitive lists of ‘k’ elements given ‘n’ things.
Please DISREGARD http://sketchtoy.com/65990621 and instead do
http://sketchtoy.com/65990767
Your work paid off – they came out looking great!
1. Yes 2. Yes 3. No 4. No 5. Yes 6. Yes 7. No 8. Yes
http://sketchtoy.com/65991519
http://sketchtoy.com/65991546
Although it t was frustrating, I enjoyed it, wish I had more time to really be creative.
I am unsure if my puzzles can be seen online, I saved them just in case they cannot.
The work in class relates to logic. The assignment of crossing a bridge without repetition is the relationship I relate to for the time I have to think about it.
I like that you used different line widths in your drawings! Your first sketch, http://sketchtoy.com/65991519, should have another point or two in the middle (so we don’t have a bridge without a point at the other end).
Part 1: 1=yes 2=yes 3=no 4=no 5=yes 6=yes 7=yes 8=yes
Part2:
http://sketchtoy.com/65992228
http://sketchtoy.com/65992254
Part3: will post additional comment
Part4: I enjoyed this assignment very much! It was super fun and interesting to do myself. A connection between this assignment and the works done in the class, I believe that in proofs/logic, we do questions that seem easy, but once we go ahead and evaluate it, we see how complex the internals really are. Also because, this assignment proves that if we map/draw things out, like the interval questions, it makes the questions easier to understand. Lastly, this assignment connects with what we are learning in class of nonrepetitive lists. Since the bridges are non-repetitive, this assignment really practices that theory.
Your first sketch made me laugh (I thought you were drawing a very, very complicated graph, until I saw the finished product)! Great.
Part 3: http://sketchtoy.com/65986088
No solution
1. #1 yes, #2 yes, #3 no, #4 no, #5 yes, #6 yes, #7 yes, #8 yes
2.http://sketchtoy.com/65992642
http://sketchtoy.com/65992660
3. I enjoyed this assignment because it made me recall my fifth grade in Music class. Actually, I saw this problem when I was in elementary school. The music teacher found this problem online and asked us to think about it. Eventually, no one solved it. After learning counting, I think we might apply counting to find how many ways we can start a point and go back to it.
1. yes, yes, no, no, yes, yes, yes, yes
2. http://sketchtoy.com/65992938
3. This is the answer to Mei Zhu’s puzzle: http://sketchtoy.com/65992660
ABCDEAC
4. This assignment was fun and out of the norm it was a puzzle. Thinking of ways to create a puzzle that is hard for someone to solve is ultimately the goal in my opinion and it was challenging. There is a connection with this and what we are learning in class. The idea of counting and not repeating ourselves. I believe it was called permutation! But yeah.
Great! But give me one more puzzle for full credit (two total).
Part1
1.yes
2.yes
3.no
4.no
5.yes
6.yes
7.yes
8.Yes
Part2
http://sketchtoy.com/65992876
no solution
Part 3
I really enjoyed this puzzele Because it challenged me to think more and this is actually what I m doing everyday, Am a yellow taxi driver and everyday I driver over
new york bridges and tunnels.
Example of today driving : I went over wiliamsburg bridge to drop off somebody at the jfk airport when I came back I took the midtwon tunnel to manhattan after that I took manhattn bridge to come to college I had a class at 10 after Class I went to laguardia airport I crossed kiowski bridge and from laguardia I had a costumer to manhattan and I crossed queensborobridge.
After a couple trips in manhattan I went back to queens crossing queensborobridge …it a lot fun driving in nyc and doing this puzzle.
The points in the puzzle simillar to sets non repetitive entries.
I love the connection to your job – it’s cool to think about this problem in real life, instead of just ‘on paper’! Give me one more puzzle for full credit (two total).
Here is my second puzzele
http://sketchtoy.com/65995082
1. yes, yes, no, no, yes, yes, yes, yes
2. http://sketchtoy.com/65993112 http://sketchtoy.com/65993188
3.
4. I really enjoyed this assignment because it involved a visualization that captured my interest that was challenging yet fun. If it was just presented to me with just points and lines i wouldn’t have found it as interesting. I find that this assignment goes well with what we are learning in class because it involves us finding and creating non repetitive lists of bridges when completing the tour.
I like your shapes!
http://sketchtoy.com/65993188
C,E,F,D,C,A,B,C
GG
part 1
1)yes 2)yes 3)no 4)no 5)yes 6)yes 7)yes 8)yes
Part 2
http://sketchtoy.com/65993416
part 4
I really enjoyed this assignment it required me to think of different ways a puzzle can be solved. this reminded me of when I was in middle school and my teacher did riddles and puzzles and the most popular puzzle he told us to try and solve was the one I posted in part 2. to solve it you must draw the shape without picking up your pen and you cannot trace over a previously drawn line.
Nice (and tricky!). Give me one more puzzle for full credit (two total).
part 3)
Answer to Sanaya’s puzzle, http://sketchtoy.com/65990624
A, E, B, F, A, B, G, C, H, D, C, B
Part 1 (EXAMPLE 4):
1. Possible.
2. Possible.
3. Impossible.
4. Impossible.
5. Possible.
6. Possible.
7. Possible.
8. Possible.
Part 2:
http://sketchtoy.com/65993616
http://sketchtoy.com/65993651
Part 3 (The solutions of Rahat’s puzzles):
Here is a puzzle: http://sketchtoy.com/65992228
Here is the solution: B,G,C,B,A,F,E,D,C.
Also, the solution for the puzzle, http://sketchtoy.com/65992254 is D,C,B,A,I,G,F,E,D,J,A,H,G.
Part 4:
I really enjoyed while I was working on this assignment because it showed me how to think critically and solved the puzzle using different steps. I think this is connected with our class work because we can solve a problem using different steps or their may not have any way to solve the problem.
1. Yes
2. Yes
3. No
4. No
5. Yes
6. Yes
7. Yes
8. Yes
http://sketchtoy.com/65993725 , http://sketchtoy.com/65993746
I enjoyed this puzzle. It’s seemingly easy but twists your brain in the same way that it’s drawn. I think the connection is the idea of combinations because starting at any given point, you are given a variety of paths. From each path will have other paths and the goal is to set the order of the list in a way that all paths(elements) are used.
Part 1: 1-yes, 2-yes, 3-no, 4-no, 5-yes, 6-yes,7-yes, 8-yes
Parts: http://sketchtoy.com/65993997
Part 4: It very interesting these puzzle. All the puzzles look reasonable and solvable, but I discover some of them short one side to completion. I had solve the puzzle with experimenting the image in my line and draw those lines in my head to see if it work. As the shape moved from being just regular square to having a bridge to connect points, it gave a opening to solving it. It very interesting puzzle, but I feel like I’m doing puzzle from newspaper.
Part 1 – there is solution to all of them except the third and fourth one.
Part 2 – http://sketchtoy.com/65995600
http://sketchtoy.com/65995680
Part 3 – I think the solution to Daniela puzzle is EDBAECA
Part 4 – I really enjoyed this assignment. It’s really fun trying to solve these puzzles. There are some puzzles I couldn’t solve, maybe because I used the wrong methods, but I think it is possible to solve. This is similar to what we did in class about repetitive and non repetitive. In the puzzles, the points can be repeated but the lines cannot.