Hi everyone,
Problem #20 in Chapter 5 uses an idea that we have *not* yet covered in class. It is no longer a required problem – you don’t have to do it – but I will give you extra credit if you turn in a solution. This is excellent practice in reading and applying a definition (just as we have been doing for the definitions of odd, even, divides, and so on). The problem relies on a new definition, that of congruence mod n – it appears in the book as Definition 5.1 on page 105, but I will also give it here:
Definition. Given integers a and b, and  , we say “a is congruent to b mod n”, or
, we say “a is congruent to b mod n”, or 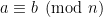 , if
, if
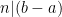 .
.
For example, if are told that 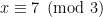 , then we can conclude:
, then we can conclude:
 (by the definition of congruence), and
(by the definition of congruence), and
 for some integer
for some integer 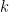 (by the definition of divides)
(by the definition of divides)
Hope this helps! Please write back and let me know if you have any questions.
Best of luck,
Prof. Reitz



