MAT2540 Discrete Structures and Algorithms II

Homework and quizzes

Posted on March 28, 2016 by Kate Poirier

As announced today in class:

You will no longer be permitted to use your homework during quizzes. You will still be able to hand in your homework for extra credit, but you must hand in your homework before a quiz begins. Quiz questions will still be selected from homework exercises, as usual, so make sure you haven’t just answered homework questions, but that you really understand your answers.

This new rule goes into effect this Wednesday, March 30 with Homework 6/Quiz 6.

Posted in Homework, Quizzes | Leave a comment

Test 1 #8 (Version A)

Posted on March 27, 2016 by Kate Poirier

Give a big-O estimate for the number of operations (where an operation is an addition or a multiplication) used in this segment of an algorithm:

$t:=1$
for $i=n$ to $n^2$
$t:= t+2it$

Explain your answer.

Here there is one loop. In this loop, there are $n^2-n+1$ instances of the value $i$ .

For each value of $i$ , there is one calculation: $t:= t+2it$ . Each such calculation uses three operations: one instance of addition and two instances of multiplication ( $(2) \cdot (i) \cdot (j)$ ).

Therefore, the total number of operations is $3(n^2-n+1)$ , which is a quadratic polynomial, so it is $O(n^2)$ .

Posted in Test #1 Solutions | 1 Comment

Test 1 #7 (Version A)

Posted on March 27, 2016 by Kate Poirier

Give a big-O estimate for the number of operations (where an operation is an addition or multiplication) used in this segment of an algorithm:

$t:=0$
for $i:=1$ to $3$
for $j:=1$ to $4$
$t:=t+ij$

Explain your answer.

There are two loops: the $i$ loop and the $j$ loop.
There are 3 values of $i$ and 4 values of $j$ so there are 12 possible pairs $(i,j)$ .

For each pair $(i,j)$ there is one calculation $t:=t+ij$ .
Each such calculation has two operations, one instance of addition and one of multiplication.

Therefore, this segment of the algorithm uses a total of 24 operations. Since 24 is a constant, the number of operations is O(1).

Posted in Test #1 Solutions | 1 Comment

Test 1 #6 (Version A)

Posted on March 27, 2016 by Kate Poirier

Let $f(x)$ and $g(x)$ be functions from the set of positive real numbers to the set of real numbers. Assume that $f(x)$ is $O(g(x))$ . Does it follow that $2^{f(x)}$ is $O(2^{g(x)}$ ? Explain your answer.

The statement is not true. To show this, we just need to find one counterexample. That is, we need to find a function $f(x)$ and another function $g(x)$ so that $f(x)$ is $O(g(x))$ but $2^{f(x)}$ is not $O(2^{g(x)}$ .

Eric posted a nice counterexample here as a correction for a Test #1 Review question.

Posted in Test #1 Solutions | 1 Comment

Test 1 #5 (Version A)

Posted on March 27, 2016 by Kate Poirier

Use the definition of big- $Theta$ notation to determine whether $f(x)=x^2$ is $\Theta(x^3)$ .

To show that $f(x)=x^2$ is $\Theta(x^3)$ , we would have to show that $f(x)=x^2$ is $O(x^3)$ and that $f(x)=x^2$ is $\Omega(x^3)$ .

However, we can see that $f(x)=x^2$ is not $\Omega(x^3)$ , as follows:

(This will be a proof by contradiction). Assume that $f(x)=x^2$ is $\Omega(x^3)$ . This means that there exists a pair of positive constants $(C,k)$ such that, for all $x>k$ , we have that $|x^2| \geq C|x^3|$ .
Since $k>0$ and $x>k$ we have that $x^2>0$ .
This means that we are assuming that $x^2 \geq Cx^3$ for all $x>k$ .
It also means that we can safely divide both sides of the inequality by $x^2$ without changing it.
This gives that $1 \geq Cx$ for all $x>k$ .
Since $C>0$ , this means that $\frac{1}{C} \geq x$ for all $x>k$ .
Whatever $C$ is, it’s just a constant, so $\frac{1}{C}$ is also just a constant. So this is saying that for all large values of $x$ , $x$ stays below the constant $\frac{1}{C}$ . This is a contradiction, so our initial hypothesis, that $f(x)=x^2$ is $\Omega(x^3)$ , must have been false.

Since $f(x)=x^2$ is not $\Omega(x^3)$ , $f(x)=x^2$ cannot be $\Theta(x^3)$ .

Posted in Test #1 Solutions | 1 Comment

Test 1 #4 (Version A)

Posted on March 27, 2016 by Kate Poirier

(a) Let $f(n)$ and $g(n)$ be functions from the set of positive integers to the set of real numbers. State the definition of the fact that $f(n)$ is $O(g(x))$ .

We say that $f(x)$ is $O(g(x))$ if there exists a pair of positive constants $(C,k)$ such that, for all $n>k$ , we have $|f(x)| \leq C|g(x)|$ .

(b) Use your definition from (a) to prove that $1^2+2^2+ \cdots n^2$ is $O(n^3)$ . Show all your work.

We want to find a pair of positive constants $(C,k)$ such that, for all $n>k$ , we have $|1^2+2^2+ \cdots n^2| \leq C|n^3|$ .

Assume that $n>1$ . Then we have $n$ inequalities.
$1^2 \leq n^2$ ,
$2^2 \leq n^2$ ,
…
$n^2 \leq n^2$ .

When we add up the left sides of these inequalities, we get $1^2+2^2+ \cdots n^2$ .
Adding up the right sides of these inequalities, we get $n^2+n^2+ \cdots n^2$ .
There are exactly $n$ terms in this expression, so $n^2+n^2+ \cdots n^2 = n(n^2)$ which is equal to $n^3$ .
This shows that $1^2+2^2+ \cdots n^2 \leq n^3$ whenever $n>1$ .
We also have that $1^2+2^2+ \cdots n^2 \geq 0$ , so this gives us that
$|1^2+2^2+ \cdots n^2| \leq |n^3|$ whenever $n>1$ .
In particular, we have that $|1^2+2^2+ \cdots n^2| \leq 1\cdot|n^3|$ whenever $n>1$ .
This proves that $1^2+2^2+ \cdots n^2$ is $O(n^3)$ , with witnesses $(C,k)=(1,1)$ .

Posted in Test #1 Solutions | 2 Comments

Test 1 #3 (Version A)

Posted on March 27, 2016 by Kate Poirier

(a) Use pseudocode to describe an algorithm for finding the largest and second largest elements in a list of integers.

procedure largest_and_2nd_largest $(a_1, a_2, \dots, a_n)$
if $a_1 > a_2$
then $max1:=a_1$
$max2:=a_2$
else $max1:=a_2$
$max2:=a_2$
for $i=3$ to $n$
if $a_i > max 1$
then $max2:=max1$
$max1:=a_i$
else if $a_i > max2$
then $max2:=a_i$
return $(max1, max2)$
{ $max1$ is the largest element in the list; $max2$ is the second-largest element in the list}

(b) Show each step of your algorithm from (a) when it is applied to the set {1, 6, 4, 2, 5}

Step 1: compare $a_1$ and $a_2$ :
Is $a_1=1 > a_2=6$ ? No, so the initial value of $max1$ is $a_2=6$ and the initial value of $max2$ is $a_1=1$ .

Step 2: $i=3$ :
Is $a_3= 4 > max1=6$ ? No.
Is $a_3=4> max2=1$ ? Yes, so we redefine $max2$ as $a_3=4$ .

Step 3: $i=4$ :
Is $a_4= 2 > max1=6$ ? No.
Is $a_4=2> max2=4$ ? No.

Step 4: $i=5$ :
Is $a_5= 5 > max1=6$ ? No.
Is $a_5=5> max2=4$ ? Yes, so we redefine $max2$ as $a_5=5$ .

The algorithm then returns $(max1, max2) = (a_2=6, a_5=5)$ .

(c) Determine the number of comparisons used by your algorithm in (a). Explain your answer. (You may ignore comparisons needed to determine whether the end of a loop has been reached.)

There is one comparison before the loop: $a_1$ versus $a_2$ .
There are $n-3+1=n-2$ values of $i$ inside the loop.
Each value of $i$ includes at most two comparisons: $a_i$ versus $max1$ and $a_i$ versus $max2$ .
Therefore there are $1 + 2(n-2)= 2n-3$ comparisons overall. (Note that this ignores comparisons needed to determine whether the end of a loop has been reached.)

Posted in Test #1 Solutions | 3 Comments

Test 1 #2 (Version A)

Posted on March 27, 2016 by Kate Poirier

(a) Use pseudocode to describe an algorithm that takes a list of $n$ integers 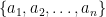$\{a_1, a_2, \dots, a_n\}$ and finds the number of integers greater than 5 in the list.

procedure greater_than_5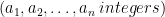 $(a_1, a_2, \dots, a_n\: integers)$
count:=0
for 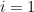$i=1$ to $n$
if $a_i > 5$
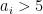
then count := count + 1
return count

(b) Show each step of your algorithm from (a) when it is applied to the set {1, 6, 4, 2, 5}.

Step 1, i=1:
Is 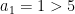$a_1=1 > 5$ ? No, so count stays at 0.

Step 2, i=2:
Is 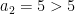$a_2=5 > 5$ ? Yes, so count is redefined as 0+1=1.

Step 3, i=3:
Is 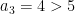$a_3=4 > 5$ ? No, so count stays at 1.

Step 4, i=4:
Is 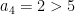$a_4=2 > 5$ ? No, so count stays at 1.

Step 5, i=5:
Is 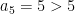$a_5=5 > 5$ ? No, so count stays at 1.

Therefore algorithm returns count = 1.

(c) Determine the number of comparisons used by your algorithm in (a). Explain your answer. (You may ignore comparisons needed to determine whether the end of a loop has been reached.)

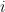The algorithm in (a) has a loop which uses $n$ values of $i$ . Each value of 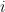$i$ gives one comparison: $a_i$ versus 5. Since there are no comparisons outside the loop, the algorithm uses $n$ comparisons. (Notice that this ignores comparisons needed to determine whether the end of a loop has been reached.)

Posted in Test #1 Solutions | 3 Comments

Test 1 #1 (Version A)

Posted on March 27, 2016 by Kate Poirier

(a) Describe in words how the binary search algorithm works:

The binary search algorithm searches for the location of a number $x$ in an ordered list of numbers $\{a_1, a_2, \dots, a_n\}$ . It first finds the element in the middle of the list (or right below the middle) and compares $x$ to this element. If $x$ is less than or equal to this middle element, then the algorithm proceeds to search in the same way in the first half of the list. Likewise, if $x$ is greater than the middle element, then the algorithm proceeds to search in the same way in the second half of the list. Either way, the algorithm cuts the list in half until there is just one element left on the list. It then compares this element to $x$ .

(b) Show each step of the binary search algorithm as it searches for 27 in the following list: {5, 6, 8, 12, 15, 21, 25, 31}.

First step: $i=1, j=8, m= \lfloor \frac{1+8}{2} \rfloor= 4, a_m=a_4= 12$ .
Since $x=27 > a_m=a_4=12$ we redefine $i=5$ and search the second half of the original list.

Second step: $i=5, j=8, m= \lfloor \frac{5+8}{2} \rfloor=6, a_m = a_6=21$ .
Since $x=27>a_m=a_6=21$ , we redefine $i=7$ and search the second half of this list.

Third step: $i=7, j=8, m= \lfloor \frac{7+8}{2} \rfloor=7, a_m = a_7=25$ .
Since $x=27>a_m=a_7=25$ , we redefine $i=8$ .

Last step: Since $i=8=j$ , we exit the loop and compare $a_8= 31$ to $x=27$ . Since $31 \neq 27$ , $x=27$ is not on the list and the algorithm returns location = 0.

Posted in Test #1 Solutions | 2 Comments

Section 11.4 – # 2 and # 6

Posted on March 27, 2016 by Eric

I chose #2 and #6 because #2 by itself didn’t feel like a review question for a test. Also they both are in sequence in the sense that they have the same instructions.

Here is a link to the solution to these two problems.

Section 11.4.2/6

CORRECTION: I apologize, I have made a mistake in the “Hint: …”. Minimum Spanning Tree refers to a tree with weights for which these problems have none. I said minimum spanning tree when I meant to say just spanning tree.

Posted in Test #2 Review | 1 Comment

Homework and quizzes

Test 1 #8 (Version A)

Test 1 #7 (Version A)

Test 1 #6 (Version A)

Test 1 #5 (Version A)

Test 1 #4 (Version A)

Test 1 #3 (Version A)

Test 1 #2 (Version A)

Test 1 #1 (Version A)

Section 11.4 – # 2 and # 6

Header Image

Recent Posts

Recent Comments

Archives

Categories

Meta

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons

The OpenLab at City Tech:A place to learn, work, and share

Support

Accessibility

Copyright

Creative Commons