Use the definition of big- notation to determine whether
is
.
To show that is
, we would have to show that
is
and that
is
.
However, we can see that is not
, as follows:
(This will be a proof by contradiction). Assume that is
. This means that there exists a pair of positive constants
such that, for all
, we have that
.
Since and
we have that
.
This means that we are assuming that for all
.
It also means that we can safely divide both sides of the inequality by without changing it.
This gives that for all
.
Since , this means that
for all
.
Whatever is, it’s just a constant, so
is also just a constant. So this is saying that for all large values of
,
stays below the constant
. This is a contradiction, so our initial hypothesis, that
is
, must have been false.
Since is not
,
cannot be
.




Many of you had the correct answer, but didn’t justify it. To show that is *not*
is *not*  , you have to show that there is *no possible pair*
, you have to show that there is *no possible pair*  such that the condition in the definition is satisfied. It’s not enough to pick a value for
such that the condition in the definition is satisfied. It’s not enough to pick a value for 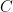 and show that it has no partner
and show that it has no partner 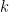 . It’s also not enough to pick a value for
. It’s also not enough to pick a value for 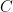 and a value for
and a value for 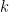 and show that they do not satisfy the condition in the definition.
and show that they do not satisfy the condition in the definition.
A few of you included a proof that is
is 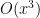 , which is true but not necessary since
, which is true but not necessary since  is not
is not  .
.