Give a big-O estimate for the number of operations (where an operation is an addition or multiplication) used in this segment of an algorithm:
for 
for 
Explain your answer.
There are two loops: the 
There are 3 values of 
For each pair 
Each such calculation has two operations, one instance of addition and one of multiplication.
Therefore, this segment of the algorithm uses a total of 24 operations. Since 24 is a constant, the number of operations is O(1).
Many of you caught that the two loops gave you 12 rounds. However, a few of you overlooked that there were two operations per round.
Some of you had the correct number of operations but didn’t include a big-O estimate for it. Some of you had the correct number of operations and included a correct–but kinda weird–big-O estimate. (For example, while 24 is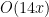
, the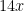 
is a sort-of random function to choose.)
Some of you were trying to count comparisons used, when that was not what the question was asking for. Don’t forget to read the question carefully. This question was copied directly from the homework, so it should not have come as a surprise.