Let and
be functions from the set of positive real numbers to the set of real numbers. Assume that
is
. Does it follow that
is
? Explain your answer.
The statement is not true. To show this, we just need to find one counterexample. That is, we need to find a function and another function
so that
is
but
is not
.
Eric posted a nice counterexample here as a correction for a Test #1 Review question.




This was one of the harder questions on the test. Since the function is increasing, it is true that if
is increasing, it is true that if 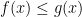 , then
, then 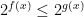 . However, it is *not* true that if
. However, it is *not* true that if  is
is  , then
, then 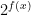 is
is 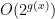 . This can be counter-intuitive if you haven’t completely understood big-O notation.
. This can be counter-intuitive if you haven’t completely understood big-O notation.
There are many different counterexamples that you can choose to see this. I saw a few others as I was grading your work, but the proofs that they were counterexamples were not always clear.