Day: April 2, 2024
The videos below all selected from this YouTube playlist, which includes additional videos.
Solving quadratic equations by factoring, i.e., using the “zero product property”:
A little tricker example of solving a quadratic by factoring–but as he notes in the video, you can also solve this using the square root property (try it!):
Completing the square:
Deriving the quadratic formula:
Using the quadratic formula:
Announcements
WebWork:
- Radical Expressions-Complex Numbers – due Wed April 3 (Sec 1.4.6)
- Quadratic Equations-Square Root – due Wed April 3 (Sec 2.2.2)
We will have a quiz tomorrow (Wed April 3), covering complex numbers and the square root property, similar to the examples we did in class and the WebWork exercises above.
The following WebWork sets are also open, on the material we covered Monday:
- Quadratic Equations-Completing the Square – due Mon April 8 (Sec 2.2.3)
- Quadratic Equations-Zero Product – due Mon April 8 (Sec 2.2.1)
Topics
We reviewed the square root property for solving quadratic equations, and introduced the technique of completing the square–together, these techniques allow us to derive the quadratic equation. We also reviewed the zero product property, which allows us to solve quadratic equations if we can factor the given quadratic polynomial:
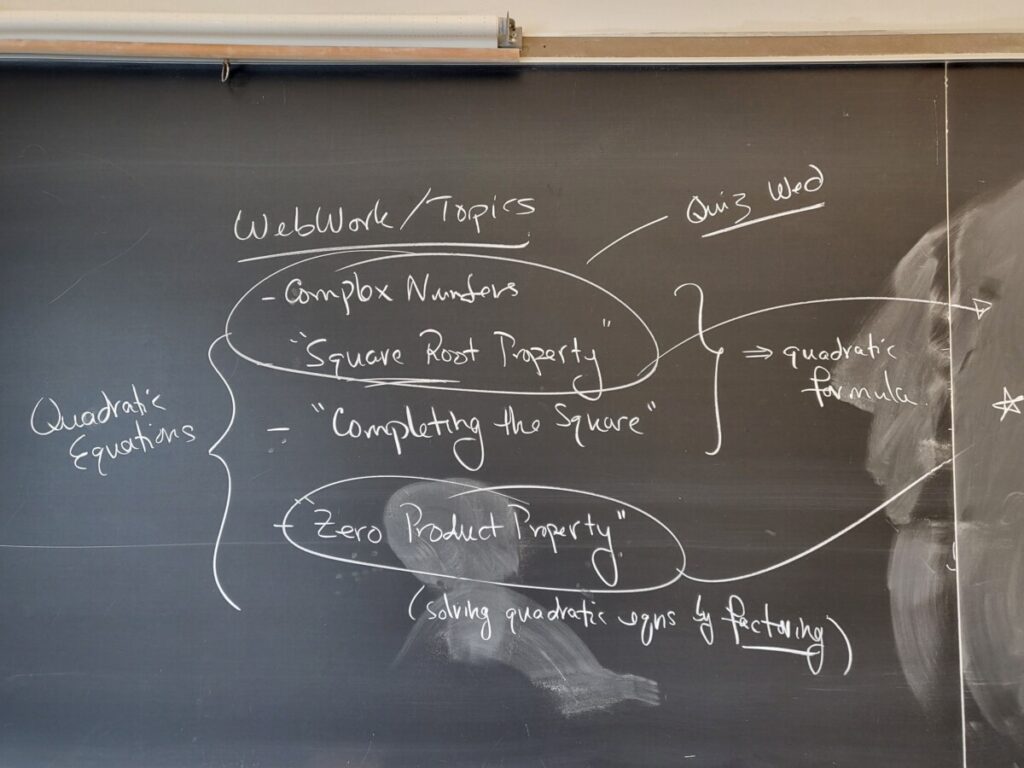
Square root property:

Introducing the technique of “completing the square” with an exercise from the WebWork: given “x^2 + bx”, we add a constant term of (b/2)^2 in order to form a perfect square trinomial (i.e., a quadratic which factors as a binomial squared: x^2 + bx + (b/2)^2 = (x + b/2)^2):

Geometric interpretation of completing the square (and of FOIL):

Another example from the WebWork:

Now we can use the technique of completing the square, followed by the square root property, to solve a given quadratic equation. Another example from the WebWork:

But note that we can solve this quadratic equation above by factoring and using the zero product property–which is quicker and simpler!

Here is an example from the WebWork where we solve the quadratic equation by completing the square (and which is not possible to factor). In fact, this quadratic equation has two complex number solutions!

Finally, we did these steps–of completing the square and applying the square root property–to an arbitrary quadratic equation of the form “x^2 + bx + c = 0” — which gives us the quadratic formula (in the case that a=1)!

The full derivation of the quadratic formula, for “ax^2 + bx + c = 0” is given at the beginning of Sec 2.2.4.



Recent Comments