
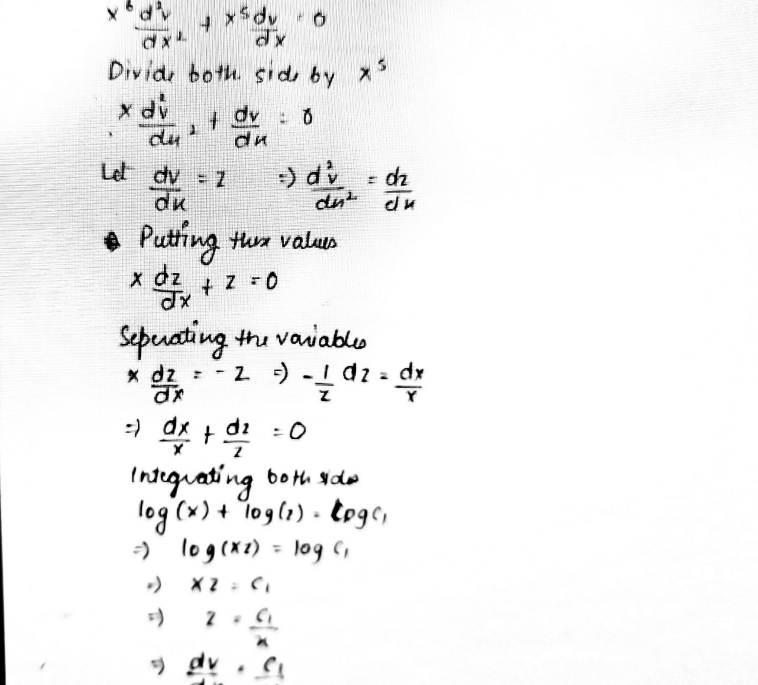
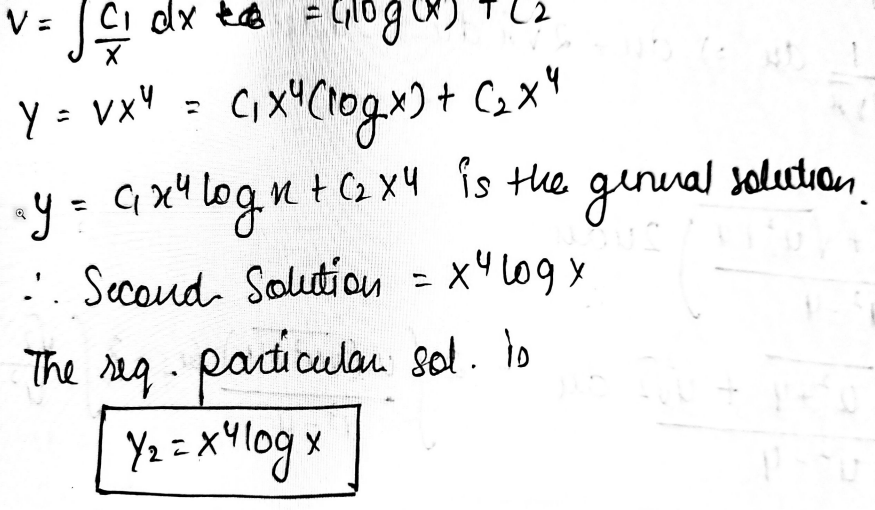
Professor Kate Poirier | D772 | Spring 2023
Test #2 Version D
Question #3
If I was stuck I would find out what type of problem I’m trying to solve. After I determined what type of problem I’m solving for, the first thing I would do is change all the y variables in for r. Now that I changed the variables it’s in a nonhomogeneous solution. I would solve for the r to get r1 and r2, which would eventually give me y1 and y2. After getting y1 and y1 you can write out a solution like Ae^(r1t) + Be^(r2t) or C1e^(r1t) + C2e^(r2t), where A, B, C1, and C2 are arbitrary constants. Second after getting y1 and y2, I would look to see which case is needed for this question. There are three cases for this question that I called Case A, Case B, and Case B. For this question it’s Case A and knowing the type of case it can help me solve for Yp. After solving for Yp I have everything I need for the general solution. The general solution is written as Yp + Ae^(r1t) + Be^(r2t) or Yp + C1e^(r1t) + C2e^(r2t).
I chose test #2 version A problem no 1
In the test, because of some calculation errors I’m unable to find the correct answer. So I’m finishing my solution here.


© 2025 MAT 2680 Differential Equations Spring 2023
Theme by Anders Noren — Up ↑
Recent Comments