The assignment below is due BEFORE CLASS on Thursday, October 8th (it is essential that you complete it before class, as we will be doing a class activity building on the assignment).
We are going to play a game creating walking tours of cities with bridges. We begin in the city of King’s Mountain, which is built on four land masses – both shores of a river and two islands in midstream – connected by a total of seven bridges (shown in green).

EXAMPLE 1: Can you create a walking tour of the city that crosses every bridge exactly once? You can begin anywhere you like, and end anywhere you like, as long as you cross each bridge just once.
Background – Graph Theory
We can simplify the picture of King’s Mountain to make it easier to deal with:
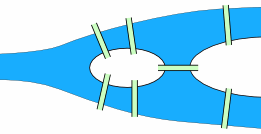
The key elements of the map are the four land masses (let’s label them A, B, C, and D) and the seven bridges (p,q,r,s,t,u and v) (thanks to mathisfun.com for the images):
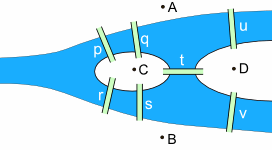
For the purposes of our problem, we can simply think about each land mass as a point (A, B, C, and D), and the bridges as lines connecting the points (p,q,r,s,t,u and v) – like this:
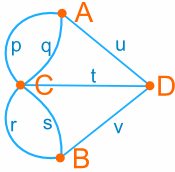
We call this kind of picture a graph – the points are called vertices and the the lines are called edges. Our goal of finding “a walking tour that crosses each bridge once” is now matter of tracing out all the edges without lifting our pencil (and without repeating any edge).
Assignment, Due Thursday 10/8 (beginning of class)
Warm up (This Warm Up is just for practice – you do NOT need to submit your answers – see below for the four-part Assignment to be submitted). The following examples build on the example above.
EXAMPLE 2: If you are given the freedom to build one new bridge in King’s Mountain (“make one new edge in the graph”), can you do it in such a way the walking tour becomes possible? Do it!
EXAMPLE 3: If you are given the freedom to destroy one bridge (“erase one edge”), can you do it in such a way that the walking tour becomes possible? Do it!
EXAMPLE 4: Construct walking tours for each of the following graphs (or decide if it is impossible).
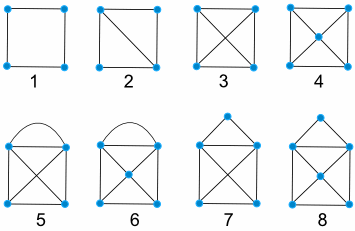
Assignment. Your assignment has 4 parts.
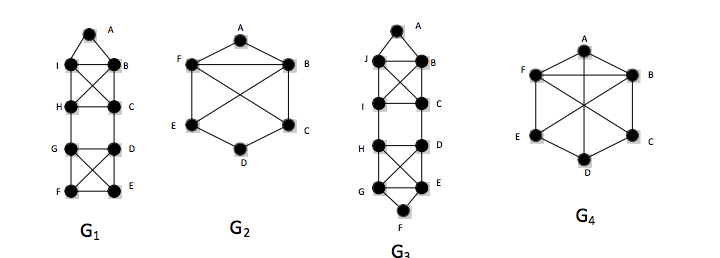
PART 1. For each of the four graphs below (G1 – G4), decide whether it is possible to create a walking tour crossing each bridge exactly once. Post your solutions here (TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER). If it is not possible to create a create a solution, say so!
PART 2. Challenge your friends: Now it’s up to you to build your own graph, and challenge your classmates to construct a walking tour (or to determine if it is impossible). It can consist of as many points as you wish, and as many bridges (edges) connecting them. You MUST label your points “A, B, C…” etc. When you’re finished, decide for yourself if a walking tour crossing each bridge exactly once is possible. Remember, the most challenging puzzles are the ones where the answer is difficult to determine. Post two puzzles in the comments. See the note “POSTING YOUR PUZZLE ONLINE” below for instructions on how to draw and share graphs online.
PART 3. Solve a friend’s puzzle. Leave a response to a friend’s posted puzzle, giving a solution. TO POST A SOLUTION, JUST LIST THE POINTS OF YOUR WALKING TOUR IN ORDER.
Example:
Here is a puzzle: http://sketchtoy.com/67467551
Here is a solution: (start at A) – A, B, D, A, E, B, C, E
PART 4. The last part of your assignment is to write a short paragraph (at least 3 sentences) responding to the following prompt. Be sure to respond to each part:
Writing Prompt: Did you enjoy this assignment? Why or why not? Describe a connection between this assignment and our work in the class. (If you don’t believe there is a connection, try to imagine why we are doing this). Leave your response in the comments.
POSTING YOUR PUZZLE ONLINE. I recommend the site sketchtoy.com – it allows you to draw something, then click “SAVE” and get a link to your drawing. If you have another (free) solution that you’d like to use, that’s fine! You can post the link in a comment, and we’ll be able to click on it and view your drawing. Don’t worry if it’s not pretty! For example, here is a graph that I drew (can you find a walking tour that crosses all edges?): http://sketchtoy.com/67467556




G1 = F-G-H-I-A-B-I-C-H-B-C-D-G-E-F-D-E
G2 = E-F-A-B-F-C-D-E-B-C
G3 = A-B-C-D-E-F-G-E-H-G-D-H-I-C-J-B-I-J-A
G4 = Not possible
Please see the attached puzzle:
http://sketchtoy.com/69352578
1st puzzle A-B-C-D-B-E-F-B-J-K-B-L-M-B-G-H-I-B-H
2nd puzzle Is there a line between A and D? If not, it is impossible.
Although I was previously familiar with the “Seven Bridges of Königsberg,” and have enjoyed these puzzles in the past, I find that I quickly get frustrated and impatient with these types of puzzles and want to find out the rule. This assignment relates to our work in class because we were presented with a statement “[t]his puzzle has a solution,” and we have to prove whether that statement is true or false.
1. G1.G2.G3 Possible G4 Not possible See
G1. E>F>D>>G>ED>C>H>B>I>IC>CB>A>L>IH>HG>GF
G2. EF>FA>AB>BF>FC>CD>DE>EB
G3. JA>AB>BJ>JC>CI>IB>BC>CD>DH>HE>EG>GD>DE>EF>FG>GH>HI
G4. AD>DE>EB>BF>FC>CB>BA>AF>FE>ED
http://sketchtoy.com/69353706
I very much enjoyed this assignment due to the fact that ive drawn these bridged networks in a previous course . Any time i start one of these in color its always interesting to see the shapes created within the exterior of the over all shape. Sometimes the way the shapes are created may hint to a certain network or bridge that must be connected. I agree with my classmate in regards to working with statements and determining whether they were true or false and if they worked.
Hey Luis. I love how challenging your puzzles are. I worked out the second one. K,L,A,B,K,D,E,F,D,C,L,B,K,F,G,H,I,J,K,H,I,F,K
I like the puzzles that you create, the first one could be : F-D-C-E-D-C-I-B-H-C-B-A-I-H-G-F
the second one is no solution .
G1:F>G,G>H,H>I,I>A,A>B,B>I,I>C,C>H,H>B,B>C,C>D,D>G,G>E,E>F,F>D,D>E
G2:E>F,F>A,A>B,B>C,C>F,F>B,B>E,E>D,D>C
G3:G,H,I,J,A,B,J,C,I,B,C,D,H,E,G,D,E,F,G
G4:no solution
I love puzzles like this, it was fun and awesome to do. In this course we are asked to find possible solutions for problems we face and we can approach solutions using different routes when possible.
G1: F-G-D-F-E-G-H-I-C-H-B-A-I-B-C-D-E
G2: E-B-F-C-B-A-F-E-D-C
G3: D-G-H-E-G-F-E-D-C-I-B-C-J-C-B-A-J-I-H-D
G4: unworkable
1: yes, 2 yes, 3no, 4 no, 5 yes , 6 no, 7 yes, 8 no.
http://sketchtoy.com/69352160
http://sketchtoy.com/69352149
I am enjoying to do these puzzles and after finish it , I am trying to find some regulations to solve the problem as ” whether there is a route for this puzzle? if not, can we add or substitute something to make it workable?” from several questions we have done, I find out if there is no route , we could add one bridge or deduct one bridge to make it workable.
I am trying to focus on the following questions: how many points is connected with odd bridges? how many points is connected with even bridges? what is the solution could be?
if there is a kind of formula, how to prove it ?
G1 = F->G->H->I->A->B->I->C->H->B->C->D->G->E-F->D->E
G2 = E->F->A->B->F->C->D->E->B->C
G3 = A->B->C->D->E->F->G->E->H->G->D->H->I->C->J->B->I->J->A
G4 = Not possible
I do like his type of problem unfortunately it takes me a lot of time to solve it. As for the link with the course the only thing that I can think of is proving something using properties of even and odd numbers. The puzzles can be solved using those properties.
This is my puzzle
http://sketchtoy.com/69356791
For your first puzzle the solution is D->B->B->C->A->B->E->D->C->E
For the first puzzle, the solution is: D>B>A>C>B>E>C>D>E
G1 E-D-G-E-F-D-C-H-B-C-I-A-B-I-H-G
G2 E-D-C-B-E-F-A-B-F-C
G3 G-F-E-H-D-E-G-D-C-I-B-C-J-A-B-J-I-H-G
I personally don’t like it at first because I am not good at this. After few days I see this post, I still struggle to find the solution. But I didn’t give up and try harder to find it.
Here is my puzzle!
http://sketchtoy.com/69354333
I really enjoyed your puzzle and I think I was able to get a solution
C,B,D,C,A,B,A,D,A
I really enjoyed your puzzle and I think I was able to get a solution
C,B,D,C,A,B,A,D,A
I really enjoyed your puzzle and I think I was able to get a solution
C,B,D,C,A,B,A,D,A
Good job, you are right!
For Ihn Lee’s puzzle:
A-C, D-B, D-C, C-B, B-D, B-A, A-D, D-A,A-B
Hi, Denyese. From ‘D-B’ to ‘D-C’, are you going back to D from B? If so, you make more than one trip for one bridge.
G1: E-G, G-D, D-F, F-E, E-D, D-C, C-I, I-B, B-H, H-C, C-B, B-A, A-I, I-H, H-G, G-F
G2: C-F, F-B, B-E, E-F, F-A, A-B, B-C, C-D, D-E
G3: E-H, H-D, D-G, G-E, E-F, F-G, G-H, H-I, I-J, J-C, C-I, I-B, B-J, J-A, A-B, B-C, C-D, D-E
G4: NO SOLUTION
This is my puzzlehttp://sketchtoy.com/69355454
At first, upon reading the assignment instructions I felt that the assignment would be one I would hate. I must say when I started it I enjoyed it thoroughly. I feel that the connection to class deals with set theory especially intersections with regards to unions and intersection.
I like your puzzle, Denyese. At first I didn’t think there was a solution, but then I realized you can:
A > E > A >D > A > C > A > B > A > F
This is my puzzle, http://sketchtoy.com/69355454
My puzzle solutions:
G1: F>E>G>D>F>G>H>C>I>H>B>I>A>B>C>D>E
G2: C>B>A>F>E>B>F>C>D>E
G3: E>F>G>D>H>E>G>H>I>C>J>I>B>J>A>B>C>D>E
G4: No solutions
I like little brain teasers and puzzles like this, so I was excited to do this assignment. I had to really rely on trial and error to find viable “walking tours” through each of the puzzles, but in the process I think I did notice one pattern that points to a rule for a solution being impossible. It seems to be the case that if a puzzle only has points which are intersected by more “bridges” than the number of other points to which those bridges are connected, then a “walking tour” is impossible. I haven’t exactly proved this to myself and I’m not sure it’s right. I think these puzzles demonstrate that it only takes one of many possible solutions to prove that something has a solution, but that finding a rule for what makes something not possible (ie false) can be a powerful way of determining exactly what makes a thing possible (ie true). In this way I think this activity relates to the way we’ve been talking about logic and to how we’ll be applying that in writing proofs.
I’ll post my puzzle later on in a separate comment.
PART 1.
G1- E,G,D,F,E,D,C,I,B,H,C,B,A,I,H,G,F
G2- C,F,B,C,D,E,B,A,F,E
G3- E,H,D,G,E,D,C,J,B,I,C,B,A,J,I,H,G,F,E
G4- NO SOLUTION
PART 2. ONE OF THESE DOESN’T HAVE A SOLUTION
http://sketchtoy.com/69357854
http://sketchtoy.com/69357860
PART 3.
COMMENT ON CLASSMATE’S PUZZLE
PART 4.
I did enjoy this assignment; I gravitate towards problem solving and patterns which I could see presented in this activity. For me it relates in that each patterns solution, or lack thereof was because of a logistical tangible reason. Even coming up with a puzzle you had to problem solve and decide if it had a solution or not.
http://sketchtoy.com/69357860
Hi, I found the solution for this.
B(loop)-A-B-C-D-E(loop)-D-A-F-B-E-F-C-E
Part I
G1: F>G>H>I>A>B>I>C>H>B>C>D>E>G>D>F>E
G2: E>F>A>B>F>C>B>E>D>C
G3: G>H>I>J>A>B>J>C>I>B>C>D>H>E>D>G>F>E
G3: It is impossible
Part III
http://sketchtoy.com/69359705
http://sketchtoy.com/69359706
Part IV
I did enjoy the assignment. It really got the brain juice pumping. I noticed that from certain vertices there were either an odd number of possible paths or an even number of possible paths. It seemed to work out, navigating once, when there were an odd number of paths. The assignment may be related to the work we have done on permutations.
Here’s my puzzle. It looks really simple, but I think it’s actually kind of tricky.
http://sketchtoy.com/69359858
G1: F—>G —>H —>I —>B —>A —>I —>C —>B —>H —>C —>D —>F —>E —>D —>G
G2: C—>F —>A —>B —>C —>D —>E —F —>B —>E
G3: H—>I —>C —>J —>B —>I —>J —>A —>B —>C —>D —>E —>H —>D —>F —>E —>G —>H
G4 is not possible.
http://sketchtoy.com/69359929
I found that assignment was enjoyable even though it took time to find out that G 4 was not possible. However, I understood that the purpose of it was to enhance our critical thinking. Since the most important part of this course is about proof, which involves critical thinking. Therefore, this assignment starts preparing us for the upcoming lesson.
http://sketchtoy.com/69360119
Had troubles posting this from my computer.
http://sketchtoy.com/69360207
This is the fixed version of it
I am having trouble articulating my path but I created videos of myself solving g1,g2,g3, g4 *I* cannot solve
part 4
I enjoyed this because I learned that I have some sort of mental disconnect between my ability to solve this sort of problem and my ability to articulate the solution. I think graphs are absolutely beautiful and look forward to learning more about them. This is very connected to what we are learning in class because math is all about relationships of objects and sets, and graphs are one way to express relationships- and Stephen Wolfram would argue the best way to order the relationships of the laws of the universe.