Hi everyone! Read through the material below, watch the videos, and follow up with your instructor if you have questions.
Lesson 4: Indexed Sets
Topic. This lesson covers:
- Sec 1.8: Indexed Sets
Learning Outcomes.
- Take unions and intersections of collections of sets indexed by the natural numbers or other sets.
Homework. There is 1 written assignment on today’s material:
- Homework: Section 1.8 p.29: 3, 5, 6, 8
Lecture Notes:
Contents
Vocabulary
- indices
- indexed sets
- index set I
Indexed Sets
Introduction
When we need to talk about a lot of different sets, instead of giving each of them different names $A, B, C, D, E, F$ it’s convenient to keep track of them by using subscript numbers, like $A_{1}, A_{2}, A_{3}, A_{4}, A_{5}$. The subscript numbers are called indexes (“indices”), and the sets are called indexed sets.
Definitions and Theorems
- Indexed sets are sets that are distinguished by attaching subscript numbers (instead of using different letters), such as $A_{1}, A_{2}, A_{3}, A_{4}, A_{5}$. We call the number $1,2,3,4$ and $5$ the indices.
- Unions and intersections of many sets. Suppose $A_{1}, A_{2}, A_{3}, \ldots, A_{n}$ are sets. Then
- $A_{1} \cup A_{2} \cup A_{3} \cup \ldots \cup A_{n}=\left\{x: x \in A_{i}\text{ for at least one set } A_{i}, \text{ for }1 \leq i \leq n\right\}$
- $A_{1} \cap A_{2} \cap A_{3} \cap \ldots \cap A_{n}=\left\{x: x \in A_{i} \text{ for every set } A_{i}, \text{ for } 1 \leq i \leq n\right\}$
- Notation. Given sets $A_{1}, A_{2}, A_{3}, \ldots, A_{n},$ we define $$\bigcup_{i=1}^{n} A_{i}=A_{1} \cup A_{2} \cup A_{3} \cup \ldots \cup A_{n} \text{ and }$$
$$\bigcap_{i=1}^{n} A_{i}=A_{1} \cap A_{2} \cap A_{3} \cap \ldots \cap A_{n}$$ - Definition. The index set $I$ is the set of all indices (of a collection of sets).
- Notation. If $I$ is an index set, and for each $\alpha \in I$ we have a corresponding set $A_{\alpha},$ then
- $\bigcup_{\alpha \in I} A_{\alpha}=\left\{x: x \in A_{\alpha}\text{ for at least one set } A_{\alpha} \text{ with }\alpha \in I\right\}$
- $\bigcap_{\alpha \in I} A_{\alpha}=\left\{x: x \in A_{\alpha}\text{ for every set } A_{\alpha} \text{ with }\alpha \in I\right\}$
Examples: Indexed Sets
Example 1: Suppose $ A_{1}=\{0,2,5\}, A_{2}=\{1,2,5\}$ and $A_{3}=\{2,5,7\}$.
Find $\bigcup_{i=1}^{3} A_{i} \text { and } \bigcap_{i=1}^{3} A_{i}$
VIDEO: Introduction to Indexed Sets, Example 1
Example 2: Consider the following infinite list of sets:
$$A_{1}={-1,0,1}, A_{2}={-2,0,2}, A_{3}={-3,0,3}, \ldots, A_{i}={-i, 0, i}, \ldots$$
Find $\bigcup A_{i} \text { and } \bigcap_{i=1}^{\infty} A_{i}$
VIDEO: Indexed Sets – Example 2
Example 3: Let the index set $I$ be the interval $[4,5),$ that is $I=[4,5)]=\{x: 4 \leq x<5\}$. For each number $\alpha \in I$, let the set $A_{\alpha}=\{x \in \mathbb{R}: \alpha \leq x \leq 6\}$.
$$\text { Find } \bigcup_{\alpha \in[4,5)} A_{\alpha} \text { and } \bigcap_{\alpha \in[4,5)} A_{\alpha}$$
VIDEO: Indexed Sets – Example 3
Introduction to Logic
The word logic refers to the way that humans reason – how we combine old information to deduce new information. It is nothing exotic – you use logic all the time in your everyday life, and certainly when you do mathematics. In Chapter 2, we will be looking at this familiar tool and studying its rules.
VIDEO: Introduction to Logic
Exit Question
Let the index set $I$ be the closed interval $[0,2]$, that is $I=[0,2]=\{x: 0 \leq x \leq 2\}$. For each number $\alpha \in I$, let the set $A_{\alpha}=\{(x, \alpha): x \in \mathbb{R}, 1 \leq x \leq 2\}$.
$$\text{ Find } \bigcup_{\alpha \in[0,2]} A_{\alpha} \text { and } \bigcap_{\alpha \in[0,2]} A_{\alpha}$$
Answer
$\bigcup_{\alpha \in[0,2]} A_{\alpha}=\{(x,y)\in\mathbb{R}^2 : 1\leq x\leq 2, 0\leq y\leq 2\}$ (shown in red in the image below). Why do the x-values range from 1 to 2 but y-values range from 0 to 2?
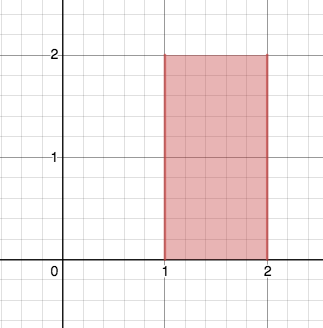
$\bigcap_{\alpha \in[0,2]} A_{\alpha} = \emptyset$. Why is this?




Re. example 4 – When explaining why the intersection of all sets in the index is an empty set, could you say this it is because each consecutive set in the index is disjointed from the previous set?
*could you say that…
Absolutely right – great explanation!