Your assignment for the coming week+ is to try to prove the conjecture that your group created in class on Thursday, 10/24. You may need to refine/expand your conjecture first (let’s discuss this in class). You must spend at least 90 minutes working on this. Trying to prove something can consist of many different activities, such as the following (you do NOT have to do all of these things – you can choose how to spend your time – they are provided for inspiration only).
- coming up with ideas, and testing them out (for example, by creating puzzles and trying to solve them)
- trying to understand what the conjecture says
- trying to solve puzzles that other people created
- trying to create puzzles (and solve them yourself)
- communicating with other members of your group (talking, emailing, etc.)
- trying to write down a proof
- other stuff…
As you work, keep track of what you are doing, thinking, and feeling (this is metacognition – an idea that discussed way back in OpenLab #2). What did you do during the time you spent? Did you create any puzzles? Did you solve puzzles? Did you change your mind about whether the conjecture is true or false? Did you have any new ideas about how to prove the conjecture? Did you have any ideas that you gave up on? How did you feel as you worked – were you frustrated/confused/happy/depressed? Why? Did your mood change along the way?
Assignment (Due Thursday, 11/7): Submit a journal of your efforts in the comments below. Your response should be at least 300 words. Describe what you did during the 90 minutes you worked, and express in some way what you were thinking and feeling during the process. Your response can include puzzles (use sketchtoy.com) or other work you did along the way.
Extra Credit. Respond to a fellow student’s comment. Did you do similar things? Different things? Do you have any suggestions for them? Be kind.
GROUP CONJECTURES (created in class 10/24):
Group 1: Song Yu, Randy, Aurkaw
Group 2: Youshmanie, Dylan


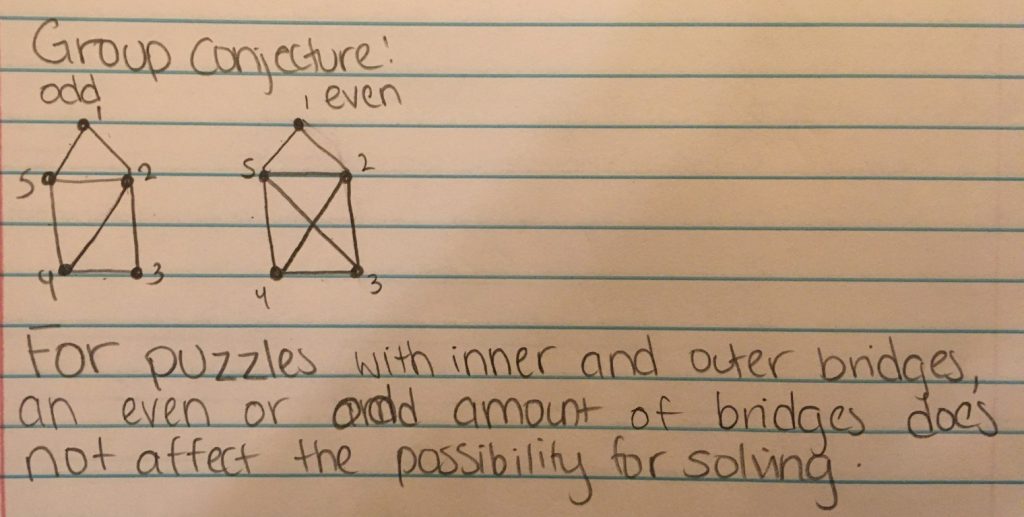



When I began working on my conjecture, I was uncertain of how to begin refining my ideas. My groups original conjecture primarily focused on puzzles having an even vs. odd amount of bridges and how this affected solvability. Therefore, I began creating puzzles with an even number of inner and outer bridges. Some of the puzzles were not solvable while others were. I then began creating puzzles with an odd number of inner and outer bridges; the first two puzzles I created for this category were both solvable. However, I realized that both puzzles were solvable because they were identical conformations of one another. While this was not intentional it led me to notice that the puzzles that were solvable also had symmetry. At this point, I became more intrigued and was interested to understand whether or not symmetry had a correlation to solvability. I first tested this idea out on puzzles that only had an odd amount of bridges but also had symmetry. After creating six puzzles of this nature I determined that each one was solvable. At this point I was excited because I believe the idea of symmetry can be implemented into our group conjecture. However, when I tested this out on puzzles with an even number of bridges, some puzzles were solvable while others were not. This was strange to me because I wondered why can the addition of just one bridge turn a puzzle that is solvable into not solvable. I am interested to determine whether the position of a bridge in an even puzzle that is symmetrical, would impact the solvability and will be thinking of ways to test this. However, at this moment I believe our conjecture can be improved by stating the following; “puzzles with an odd number of inner and outer bridges which are also symmetrical, are solvable.”
When I began working on my conjecture, I was uncertain of how to begin refining my ideas. My groups original conjecture primarily focused on puzzles having an even vs. odd amount of bridges and how this affected solvability. Therefore, I began creating puzzles with an even number of inner and outer bridges. Some of the puzzles were not solvable while others were. I then began creating puzzles with an odd number of inner and outer bridges; the first two puzzles I created for this category were both solvable. However, I realized that both puzzles were solvable because they were identical conformations of one another. While this was not intentional it led me to notice that the puzzles that were solvable also had symmetry. At this point, I became more intrigued and was interested to understand whether or not symmetry had a correlation to solvability. I first tested this idea out on puzzles that only had an odd amount of bridges but also had symmetry. After creating six puzzles of this nature I determined that each one was solvable. At this point I was excited because I believe the idea of symmetry can be implemented into our group conjecture. However, when I tested this out on puzzles with an even number of bridges, some puzzles were solvable while others were not. This was strange to me because I wondered why can the addition of just one bridge turn a puzzle that is solvable into not solvable. I am interested to determine whether the position of a bridge in an even puzzle that is symmetrical, would impact the solvability and will be thinking of ways to test this. However, at this moment I believe our conjecture can be improved by stating the following; “puzzles with an odd number of inner and outer bridges which are also symmetrical, are solvable.”
My first conjecture I made on my own, for the first part of this many part project, consisted of an idea about a starting point to solve a diagram without crossing paths twice. That idea was that we would have to start at a vertex with an odd number of connecting points. My partner Song Yu also came up with something very similar to mine. It felt nice to know that we were both probably headed in the right direction, so we came up with a conjecture together including both of our ideas. Our conjecture was “If the diagram only has [an] even [amount of] connecting points, then a starting point can be anywhere. If the diagram has both an even and an odd number of connecting points [vertices] then the starting and endpoint will be at [a position where] an odd number of connecting points [vertex lies]”. While doing this journal, I realized that this wasn’t really the case because some diagrams weren’t solvable even if I chose a vertex with an odd number of adjacent lines. After playing a lot with sketchtoy.com, I realized that only some diagrams I drew out were solvable even when I chose a vertex with odd adjacent lines. It bothered me because I couldn’t figure out why that was the case, where some diagrams would work and some wouldn’t. I continued to listen to the music I was already listening to just try to clear my brain and start fresh. I was about to take a little time off on working on this conjecture until I had the idea to use what we learned in class and to try to deal with this problem by case.
Case 1: Where a diagram has a greater number of vertices with an even number of adjacent lines.
Case 2: Where a diagram has a greater number of vertices with an odd number of adjacent lines.
Case 3: Where a diagram has an equal number of vertices with odd and even adjacent lines
After playing with sketchtoy I came to the conclusion that Case 1 and 3 always gave me a solvable diagram. Case 2 always failed and gave me no solution. I then went back to an earlier open lab assignment where we had to solve the diagrams and write down its paths. I realized the first three were solvable because it followed either case 1 or case 3. The last diagram was not solvable because it followed case 2. Thus I came up with a new conjecture:
– A diagram is solvable when a diagram has a greater than or equal to a number of vertices with an even number of adjacent lines than the number of vertices with an odd number of adjacent lines.
http://sketchtoy.com/69053410
^^^ this is the link to sketchtoy where I played around for a bit to figure this out
I agree with the method of direction you were going in by making a ton of examples and making cases was awesome. Some thing I did differently was that I started for basic which could be a problem but I gradually made more complex and I will u your sketchtoy as examples to skip the in between a bit. Some advice I would give is start small. People like to jump straight to the answer but often in math the answer to the hardest questions are the simple things if that makes any sense.
Given two points connected by an edge can be solved in which the starting place doesn’t matter. Three points connected by 2 edges can be solved but only if you do not start at the middle point. A triangle, square and rectangle can be solved starting at any point. Two triangles glued together at any side is solve no matter where you start. Drawing any n-sided shape is possible so long as for every point it has a maximum of 2 edge connections. A square with two diagonals is never possible. My approach right now is to focus primarily on the the difference n-shapes that are possible and I am labeling the next of edges attached to each and every point which should be two and at this point 100% possible. Then I am drawing one edge to it while keeping track of a edges assign to a point. There are patterns unless I am mistake but for a square with every point has 3 edges it is impossible and a pentagon with 3,3,3,3,2 pattern is always impossible. This is why I am thinking that there is a pattern that is not easy to see such that the combination of edges to point ratio plays an super important factor in which it is solvable. A puzzle having even or an odd amount of edges can some times be solved so that means that the parity of even and odd doesn’t affect if it is solvable. This is proven in making any n-sides shape in which we break in down in to two cases. N is odd or n is even. Triangles and squares are both possible. One is with even number of edges and the other with odd number of edges. Let’s focus on a pentagon 2,2,2,2,2 which is always possible. Add one more edge 3,3,2,2,2 is also always possible. One more edge than and we get 4,3,3,2,2 then 3,3,3,3,2 then 4,4,2,2,2 and I can conclude that 3,3,3,2,2 is impossible matter the order so long as the points follow that pattern but on the other hand if they follow a 4,3,3,2,2 or a 4,4,2,2,2 pattern than is will always be possible. In this string I think there can also be a pattern to be found because I know let’s say 5,5,4,4,2,2 is possible than all of this pattern is true than once o find out the pattern that makes this true than I will be good. Here are the possible reasons a pattern may be possible to make:
1. The sum of the even numbers is greater than the odd numbers
2. Their are more even numbers than odd numbers
3. There are not odd number of odd numbers in a row
4. There are more even numbers in a row than odd numbers in a row
5. Some reason I am now thinking of because my list is too short
When I worked on my group conjecture, I didn’t know how to began it. The idea of my group conjecture is difficult to understand by looking at words. So I used some puzzles from the past assignment and I try to create puzzles on my own. I observed that our conjecture would be true by looking at past assignments. Nevertheless, it is false for the puzzle I created; there would have a situation that some puzzles show no solution. After I drew more puzzles, I figured out the number of vertices of odd number lines must be either zero or two, if more than that, there will be no solution. For example, http://sketchtoy.com/69053527. In this puzzle I created, there are more than two vertices with odd number lines and I couldn’t find the solution to this. Our conjecture assumes that “if a diagram has both even number and the odd number of connecting lines, then the starting point and endpoint will be at an odd number of connecting lines.” Therefore, the starting and ending vertices will be the two vertices with odd number lines. However, I am not sure what happens if all vertices with even number lines. So, I created some puzzles to support our conjecture, it shows we can get the starting and ending vertices everywhere. For example, http://sketchtoy.com/69053535. In this example, all vertices with even numbers lines and can find starting and ending vertices anywhere. Based on the puzzles I working with, it supports our group conjecture is true. Later on, I spend a long time to thought about how to put all the information to make our conjecture reasonable. The conjecture will be long-drawn if I just put all the information together. I am not sure how to write it down now.
I had no idea how to do this conjecture. I just came up with several classes of graphs, and see whether a trip can be made. First, I considered so-called line graphs. These are graphs of n points, (n being a natural number), arranged in a line. I conjectured that a trip is possible precisely when you start at one of the endpoints. It is easy to see that my conjecture is true. Then I considered star graphs. Let n be a natural number greater than or equal to 3. The graph S_n, is 1 point, the center of the star, connected to n other points, with no other connections. I conjectured that no trip is possible for any star graph, no matter where you start. It is easy to see that my conjecture is true. Then I considered cyclic graphs. Let n be a natural number greater than or equal to 3. The graph C_n is n points arranged in a cyclic order. It is just a line graph, with the connection between the first and the last point added. I conjectured that a trip is possible for any cyclic graph, no matter where you start. It is easy to see that my conjecture is true. The last class of graphs I considered are wheel graphs. They are somewhat like a fusion of a cyclic and a star graph. Let n be a natural number greater than or equal to 3. The graph W_n, is n points arranged in a regular polygon, with the addition of the central point, and connections between the n points and the central point, and no other connections. I conjecture that no trip is possible for any wheel graph, no matter where you start. I verified this for W_3. I don’t know how to prove this conjecture.